Основные определения экспериментально статистических методов математического моделирования.

В тех случаях, когда информации о рассматриваемом процессе недостаточно или процесс настолько сложен, что невозможно составить его детерминированную модель, прибегают к экспериментально-статистическим методам. Процесс при этом рассматривают как «черный ящик». Различают пассивный и активный эксперимент.

Пассивный эксперимент является традиционным методом, когда ставится большая серия опытов с поочередным варьированием каждой из переменных; к пассивному эксперименту относится также сбор исходного статистического материала в режим нормальной эксплуатации на промышленном объекте. Обработка опытных данных в этом случае для получения математической модели проводится методами классического регрессионного и корреляционного анализа.

Активный эксперимент ставится по заранее составленному плану (планирование эксперимента), при этом предусматривается одновременное изменение всех параметров, влияющих на процесс, что позволяет сразу установить силу взаимодействия параметров и поэтому сократить общее число опытов.

Используя при обработке опытных данных принципы регрессионного и корреляционного анализа, удается найти зависимость между переменными и условиями оптимума. В обоих случаях математической моделью является функция отклика, связывающая параметр оптимизации, характеризующий результаты эксперимента, с переменными параметрами, которыми экспериментатор варьирует при проведении опытов:

Принято называть независимые переменные х₁, х₂, ..., х_к. факторами, координатное пространство с координатами х₁, х₂, ..., х_к — факторным пространством, а геометрическое изображение функции отклика в факторном пространстве — поверхностью отклика.

При использовании статистических методов математическая модель представляется в виде полинома — отрезка ряда Тейлора, в который разлагается неизвестная зависимость

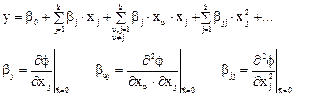
В связи с тем, что в реальном процессе всегда существуют неуправляемые и неконтролируемые переменные, изменение величины носит случайный характер. Поэтому при обработке экспериментальных данных получаются так называемые выборочные коэффициенты регрессии b₀,b_j b_uj, b_jj, являющиеся оценками теоретических коэффициентов β₀ β_j β_uj β_jj. Уравнение регрессии, полученное на основании опыта, запишется следующим образом:

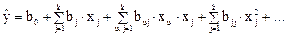
Коэффициент b₀ называют свободным членом уравнения регрессии; коэффициенты b_j —линейными эффектами; коэффициенты b_jj—квадратичными эффектами; коэффициенты b_uj — эффектами взаимодействия. Коэффициенты уравнения определяются методом наименьших квадратов из условия:

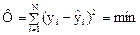
Здесь N — объем выборки из всей совокупности значений исследуемых параметров. Разность между объемом выборки N и числом связей, наложенных на эту выборку l, называется числом степеней свободы выборки f:

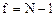
При отыскании уравнения регрессии число связей равно числу определяемых коэффициентов.

Вид уравнения регрессии выбирается путем экспериментального подбора.