Методы регрессионного и корреляционного анализа.
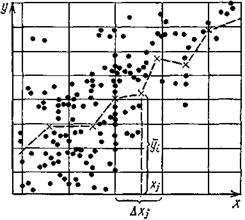
Рис. 1. Корреляционное поле.
При изучении зависимости от одного переменного параметра полезно для определения вида уравнения регрессии построить эмпирическую линию регрессии. Для этого весь диапазон изменения х на поле корреляции разбивается на равные интервалы Δх. Все точки, попавшие в данный интервал Δхj, относят к его середине xj. Для этого подсчитывают частные средние y, для каждого интервала:
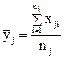
Здесь nj—число точек в интервале Δхj.
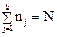
где k—число интервалов разбиения; N—объем выборки.
Затем последовательно соединяют точки (хj, уj) отрезками прямой. Полученная ломаная линия называется эмпирической линией регрессии у по х. По виду эмпирической линии регрессии можно подобрать уравнение регрессии 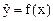 .
.
Задача определения параметров уравнения регрессии сводится практически к определению минимума функции многих переменных. Если 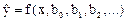 , есть функция дифференцируемая и требуется b0, b1, b2,… выбрать так, чтобы
, есть функция дифференцируемая и требуется b0, b1, b2,… выбрать так, чтобы
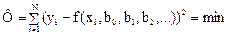
необходимым условием минимума Ф(b0, b1, b2,….) является выполнение равенств 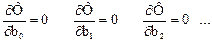
или
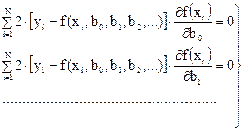
После преобразований получим:
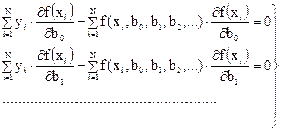
Система, уравнений содержит столько же уравнений, сколько неизвестных коэффициентов b0, b1, b2,…. входит в уравнение регрессии и называется в математической статистике системой нормальных уравнений.
Величина Ф ≥ 0 при любых b0, b1, b2,….; следовательно, у нее обязательно должен существовать хотя бы один минимум. Поэтому, если система нормальных уравнений имеет единственное решение, то оно и является минимумом для величины Ф. Решать систему в общем виде нельзя. Для этого надо задаться конкретным видом функции f.
Для оценки силы линейной связи вычисляется выборочный коэффициент корреляции r*:
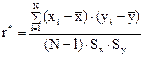
где Sx, Sy—выборочные среднеквадратичные отклонения.
После того как уравнение регрессии найдено, необходимо провести статистический анализ результатов. Этот анализ состоит в следующем: проверяется значимость всех коэффициентов регрессии в сравнении с ошибкой воспроизводимости и устанавливается адекватность уравнения. Такое исследование носит название регрессионного анализа.
Оценка тесноты нелинейной связи. Если считать, что уравнение регрессии найдено с достаточной точностью, то остаточная дисперсия обусловлена только наличием дисперсии воспроизводимости, т. е.
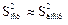
Чем меньше доля Sост2 в общей дисперсии S2y тем сильнее связь между у и х, ибо тем меньше доля случайности в этой связи. Поэтому силу связи можно характеризовать величиной
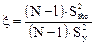
Связь тем сильнее, чем меньше ξ. Величина
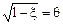
называется корреляционным отношением. Чем больше θ, тем сильнее связь
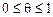
Если θ = 1, существует функциональная зависимость между параметрами. При θ = 0, однако, величины у и х нельзя считать независимыми, так как связь между ними, не сказываясь на дисперсиях, может проявить себя в моментах более высокого порядка. Только в случае нормального распределения равенство нулю корреляционного отношения однозначно свидетельствует об отсутствии связи между случайными величинами. Корреляционное отношение, как и коэффициент корреляции в линейной регрессии, характеризует тесноту связи между случайными величинами. Вообще анализ силы связи по θ называют корреляционным анализом.
В случае линейной регрессии корреляционное отношение равно коэффициенту корреляции:
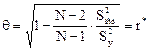
Дата добавления: 2015-03-03; просмотров: 1184;
