Метод моментов.

Основные свойства распределения случайной величины значительно проще можно описать несколькими числовыми характеристиками, которые с помощью чисел определяют наиболее существенные особенности распределения. Такой системой характеристик являются моменты случайной величины.

Моменты систематизируются по трем признакам: порядку момента β, началу отсчета случайной величины и виду случайной величины.

Порядок момента β может быть любой целой величиной; практически же рассматривают моменты нулевого, первого, второго, третьего и четвертого порядков, т. е. β = 0, 1, 2, 3, 4.

По началу отсчета случайной величины моменты могут быть начальными и центральными, а по виду — характерными для дискретных и непрерывных величин.

Начальным моментом β-го порядка для дискретных величин называется выражение

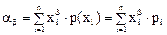
При уменьшении расстояния между соседними величинами дискретная величина будет стремиться перейти в непрерывную. При этом

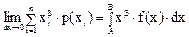
где А и В— нижний и верхний пределы возможных значений случайной величины х; f(x)—плотность распределения.

Таким образом, можно записать, что начальный момент β-го порядка для непрерывной величины равен:

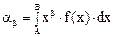
Рассмотрим начальные моменты непрерывных величин. Начальный момент нулевого порядка, или нулевой начальный момент, равен:

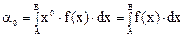
Но ранее было установлено, что следовательно, нулевой начальный момент α₀=l и характеризует площадь, находящуюся под кривой распределения.

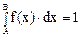
Начальный момент первого порядка, или первый начальный момент характеризует значение случайной величины, вокруг которою, группируются все возможные ее значения, т. е. определяющим координаты центра группирования; его называют средним значением или математическим ожиданием случайной величины.

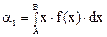
Для случайной величины X принято обозначение α₁ = m_х. Величина m_х имеет ту же размерность, что и величина X. Графики распределений, имеющих значения математического ожидания m_X2>m_X1, приведены на рис. 1.

Из рис. 1. видно, что математическое ожидание, или среднее значение, является той числовой характеристикой, которая определяет центр группирования случайной величины. Центр группирования часто принимают за начало отсчета, что равносильно переносу начала координат в точку m_х.

Случайные величины, отсчитываемые от центра группировки, т. е. от математического ожидания, называются центрированными. Моменты центрированной величины называются центральными.

Переход от начальных моментов к центральным осуществляется заменой для дискретных величин значения x_i на (x_i—m_x), а для непрерывных величин заменой величины x на (х—m_х). Так, для непрерывных величин можно записать следующее.

Нулевой центральный момент

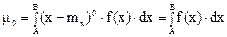
но ранее было установлено, что

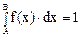
следовательно, μ₀=1 и выражает площадь под кривой распределения.

Первый центральный момент

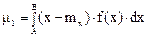или

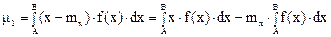
и учитывая, что

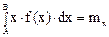и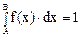

получим:

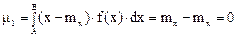
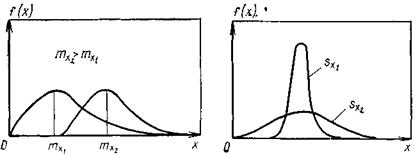
Рис. 1. Функция плотности распределения и математическое ожидание

Рис. 2. Функции плотности распределения для различных значений вторых центральных моментов (дисперсий)

Откуда следует, что математическое ожидание центрированной величины равно нулю.

Второй центральный момент (рис. 2.)

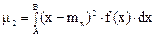
характеризует рассеяние случайной величины относительно среднего значения и называется дисперсией, обозначаемой через μ₂=S²_x , так как имеет размерность квадрата случайной величины.

Извлекая квадратный корень из дисперсии, получаем среднее квадратичное отклонение случайной величины X:

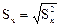
Для наглядности на рис. 2. показана плотность распределения для различных S_k, причем S_X2>S_Xl.

Таким образом, положение кривой распределения характеризуется величиной математического ожидания m_x, а степень разбросанности параметров — величиной дисперсии S²_x

Для более полного описания распределения параметров применяются также моменты высших порядков.

Третий центральный момент

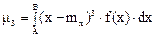
характеризует скошенность, или асимметрию распределения Безразмерный коэффициент асимметрии вычисляется как

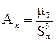
На рис. 3. представлены два асимметричных распределения: одно из них (кривая 1) имеет положительную асимметрию, другое (кривая 2)—отрицательную. Четвертый центральный момент

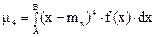
характеризует «крутость» распределения, т. е. островершинность или плосковершинность распределения. Эти свойства распределения описываются с помощью безразмерной величины, так называемого эксцесса:

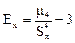
Число 3 вычитается из отношения μ₄/S⁴_x потому, что для весьма важного и широко распространенного в природе нормального распределения μ₄/S⁴_x = 3. Следовательно, для нормального распределения эксцесс Е_х = 0. Кривые, более островершинные по сравнению с нормальной, обладают положительным эксцессом, а кривые, более плосковершинные, — отрицательным эксцессом (рис. 4).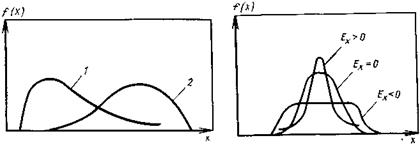

Рис. 3. Функции плотности распределения для различных значений третьих центральных моментов:

1 — при положительной асимметрии; 2 — при отрицательной асимметрии.

Рис. 4. Функции плотности распределения для различных значений четвертых центральных моментов

Соотношения между начальными и центральными моментами. Установим соотношения на примере второго момента. Из предыдущего

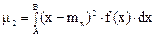
Возводя в квадрат и представляя равенство в виде суммы интегралов, получим:

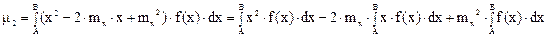
Обозначая

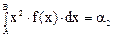и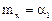

а также учитывая, что после подстановки

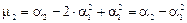
для остальных центральных моментов по аналогии будем иметь:

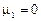
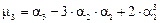
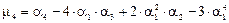
Приведенные соотношения справедливы как для непрерывных, так и для дискретных величин.

На практике при статистической обработке данных обычно ограничиваются определением первого и второго моментов, т. е. математического ожидания и среднеквадратичного отклонения, однако для более полной характеристики распределения целесообразно находить все четыре момента.