Определение коэффициентов уравнения регрессии методом Брандона.
По этому методу уравнение регрессии записывается в виде:
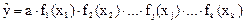
где 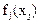 - любая функция величины xj.
- любая функция величины xj.
Порядок расположения факторов x1, x2, … xk в выражении не безразличен для точности обработки результатов наблюдений: чем больше влияние на у оказывает параметр xj , тем меньше должен быть порядковый номер индекса j. Вид функции выбирается с помощью графических построений. Вид функции выбирается с помощью графических построений. Вначале по точкам выборки системы величин y, x1, x2, … xk строятся поле корреляции и эмпирическая линия регрессии y-x1 . Таким образом определяется тип зависимости
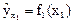
и методом наименьших квадратов рассчитываются коэффициенты этого уравнения регрессии. Затем составляется выборка новой величины
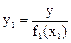
Эта величина не зависит уже от х1 , а определяется только параметрами x2, x3, … xk. Поэтому можно записать
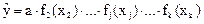
По точкам новой выборки величин y1 и х2 вновь строятся корреляционное поле и эмпирическая линя регрессии, характеризующая зависимость y1 от х2 :
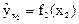
Рассчитываются ее коэффициенты и вновь составляется выборка новой величины
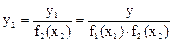
Эта величина не зависит уже от двух факторов x1 и x2 и может быть определена из следующего уравнения регрессии:
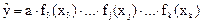
Такая процедура определения функций продолжается до получения выборки величины:
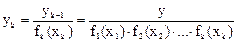
Эта величина не зависит от всех факторов x1, x2, … xk и определяется коэффициентом исходного уравнения:
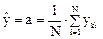
где N – объем выборки.
Методы планирования экспериментов.
Методы планирования экспериментов позволяют свести к минимуму число необходимых опытов и одновременно выявить оптимальное значение искомой функции.
Оптимальный двухуровневый план 2к.
При планировании экспериментов условия опытов представляют собой фиксированное число значений уровней для каждого фактора. Если эксперименты проводятся только на двух уровнях, при двух значениях факторов, и при этом в процессе эксперимента осуществляются все возможные комбинации из k факторов, то постановка опытов по такому плану носит название полного факторного эксперимента (ПФЭ) или плана 2k.
Уровни факторов представляют собой в этом случае границы исследуемой области по данному технологическому параметру. Пусть, например, изучается влияние на выход продукта у трех факторов: температуры Т в диапазоне 100—200 ºС, давления Р в диапазоне 2—6 МПа == (20—60 кгс/см2) и времени пребывания t = 10— 30 мин. Верхний уровень по температуре z1max = 200 °С, нижний; z1min = 100 °С, z10 = 150 °С, Δz1 = 50 °С:
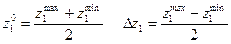
Вообще для любого фактора zj имеем:
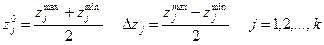
Точка с координатами (z10, z20, … ,zk0) носит название центра плана, иногда ее называют основным уровнем; , Δzj - единица варьирования, или интервал варьирования по оси zj. От системы координат z1, z2 z3, ..., zk перейдем к новой безразмерной системе координат x1, x2, …. , xk. Формула перехода (кодирования)
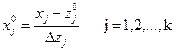
В безразмерной системе координат верхний уровень равен +1 нижний равен - 1, координаты центра плана равны нулю и совпадают с началом координат. В нашей задаче k = 3. Число возможных комбинаций N из трех факторов на двух уровнях равно N = 2k == 23 = 8. Запишем план проведения экспериментов (матрицу планирования) в виде таблицы.
| Значение факторов в натуральном масштабе | Значение факторов в безразмерной системе координат | Выход | |||||
| № опыта | z10 | z20 | z30 | х1 | х2 | х3 | y |
| -1 | -1 | -1 | |||||
| +1 | -1 | -1 | |||||
| -1 | +1 | -1 | |||||
| +1 | +1 | -1 | |||||
| -1 | -1 | +1 | |||||
| +1 | -1 | +1 | |||||
| -1 | +1 | +1 | |||||
| +1 | +1 | +1 |
Значения выхода у, полученные в результате реализации плана экспериментов, приведены в последнем столбце таблицы.
Представленный в табл. кодированный план геометрически может быть интерпретирован в виде куба, восемь вершин которого, представляют собой восемь экспериментальных точек.
Запишем кодированную матрицу планирования 23 и результаты эксперимента, введя столбец так называемой фиктивной переменной x0=1.
Приведенная в таблице матрица планирования обладает следующими свойствами:
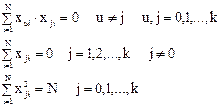
где k — число независимых факторов; N — число опытов в матрице планирования.
Первое свойство - равенство нулю скалярных произведений всех вектор - столбцов - называется свойством ортогональности матрицы планирования. Благодаря этому свойству резко уменьшаются трудности, связанные с расчетом коэффициентов уравнения регрессии, так как матрица коэффициентов нормальных уравнений (Х*Х) становится диагональной и ее диагональные элементы равны числу опытов в матрице планирования N. Диагональные элементы обратной матрицы (Х*Х)-1:
Сjj = 1/N
| № опыта | х0 | х1 | х2 | х3 | y |
| +1 | -1 | -1 | -1 | y1 | |
| +1 | +1 | -1 | -1 | y2 | |
| +1 | -1 | +1 | -1 | y3 | |
| +1 | +1 | +1 | -1 | y4 | |
| +1 | -1 | -1 | +1 | y5 | |
| +1 | +1 | -1 | +1 | y6 | |
| +1 | -1 | +1 | +1 | y7 | |
| +1 | +1 | +1 | +1 | y8 |
Следовательно, любой коэффициент уравнения регрессии bjопределяется скалярным произведением столбца у на соответствующий столбец xj, деленным на число опытов в матрице планирования N:
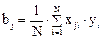
Пользуясь планом, представленным в таблице, сначала вычислим коэффициенты регрессии линейного уравнения
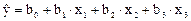
Если в рассмотрение ввести более полное уравнение регрессии с коэффициентами взаимодействия:
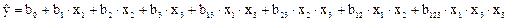
то для определения коэффициентов b12, b13, b23 (эффектов двойного взаимодействия) и b123 (эффекта тройного взаимодействия) необходимо расширить матрицу таблицы следующим образом:
| № опыта | х0 | х1 | х2 | х3 | х1 х2 | х1 х3 | х2 х3 | х1 х2 х3 | y |
| +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | ||
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | ||
| +1 | -1 | +1 | -1 | +1 | +1 | +1 | +1 | ||
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | ||
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | ||
| +1 | +1 | -1 | +1 | -1 | +1 | +1 | -1 | ||
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | ||
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
Если поставить дополнительно параллельные опыты, можно определить S2воспр , проверить значимость коэффициентов регрессии и при наличии степеней свободы - адекватность уравнения.
В связи с тем, что корреляционная матрица (Х*Х)-1 для спланированного эксперимента таблица есть матрица диагональная
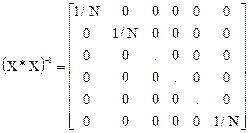
коэффициенты уравнения регрессии некоррелированы между собой. Значимость коэффициентов уравнения регрессии можно проверять для каждого коэффициента в отдельности по критерию Стьюдента. Исключение из уравнения регрессии незначимого коэффициента не скажется на значениях остальных коэффициентов. При этом выборочные коэффициенты bj оказываются так называемыми несмешанными оценками для соответствующих генеральных коэффициентов βj.
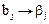
т. е. величины коэффициентов уравнения регрессии характеризуют вклад каждого фактора в величину у.
Диагональные элементы корреляционной матрицы равны между собой, поэтому все коэффициенты уравнений определяются с одинаковой точностью:
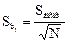
Дата добавления: 2015-03-03; просмотров: 2575;
