Закон полного тока для магнитного поля в вакууме
(теорема о циркуляции вектора В)
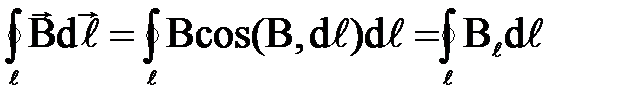
 В разделе “Электростатика” было доказано, что циркуляция вектора напряженности электростатического поля вдоль замкнутого контура равна нулю, откуда следует потенциальный характер электростатического поля. Одним из основных отличий магнитного поля от электростатического поля является его непотенциальность. Для доказательства этого рассмотрим линейный интеграл от В по замкнутому пути в магнитном поле, создаваемом током, т.е.
В разделе “Электростатика” было доказано, что циркуляция вектора напряженности электростатического поля вдоль замкнутого контура равна нулю, откуда следует потенциальный характер электростатического поля. Одним из основных отличий магнитного поля от электростатического поля является его непотенциальность. Для доказательства этого рассмотрим линейный интеграл от В по замкнутому пути в магнитном поле, создаваемом током, т.е.
где 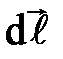 – вектор элемента длины контура, направленный вдоль обхода контура; Вℓ – проекция вектора
– вектор элемента длины контура, направленный вдоль обхода контура; Вℓ – проекция вектора 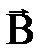 на направление касательной к контуру. Данный интеграл называется циркуляцией вектора
на направление касательной к контуру. Данный интеграл называется циркуляцией вектора 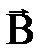 по заданному замкнутому контуру ℓ.
по заданному замкнутому контуру ℓ.
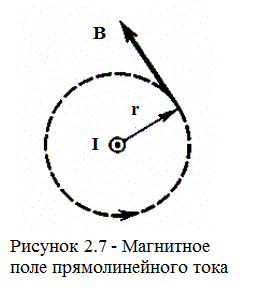
Рассмотрим частный случай: круговой путь ℓ является силовой линией радиуса R магнитного поля прямолинейного бесконечного проводника с током (рис.2.7).
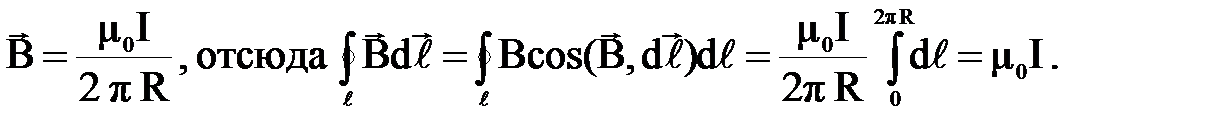
Магнитная индукция для этого случая была подсчитана ранее, и во всех точках окружности вектор 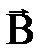 составляет:
составляет:
Угол между векторами 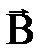 и
и 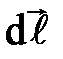 равен нулю, поэтому cos(
равен нулю, поэтому cos( 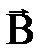 ,
, 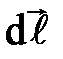 )=1. Из полученного результата следует, что циркуляция вектора магнитной индукции вдоль силовой линии прямолинейного проводника с током не равна нулю, т.е. поле такого проводника непотенциально. Оно называется вихревым. Полученная формула справедлива для любой формы замкнутого контура, охватывающего проводник с током.
)=1. Из полученного результата следует, что циркуляция вектора магнитной индукции вдоль силовой линии прямолинейного проводника с током не равна нулю, т.е. поле такого проводника непотенциально. Оно называется вихревым. Полученная формула справедлива для любой формы замкнутого контура, охватывающего проводник с током.
Пусть теперь наш контур ℓ произвольной формы охватывает n проводников с токами I1, …In. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. При этом положительным считается ток, если он с направлением обхода контура образует правовинтовую систему. Ток противоположного направления считается отрицательным.
| Рисунок 2.8 - Определение полного тока |
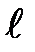
|
| I2 |
| I1 |
| I3 |
| I4 |
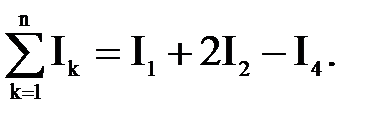
Ток I3 не учитывается, т.к. он не охватывается контуром. В результате имеем
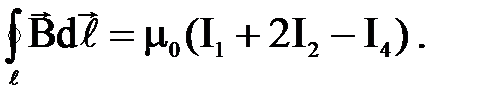
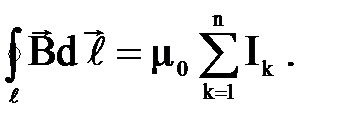
Таким образом, циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром:
Данное выражение представляет собой закон полного тока для магнитного поля в вакууме, или теорему о циркуляции вектора В.
Все вышерассмотренное относится к вакууму. Можно доказать, что циркуляция вектора 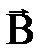 вдоль замкнутого контура, не охватывающего проводник с током, равна нулю.
вдоль замкнутого контура, не охватывающего проводник с током, равна нулю.
Рассмотренная нами теорема имеет в магнитостатике такое же значение, как теорема Гаусса в электростатике. Она позволяет находить магнитную индукцию различных полей без применения закона Био-Савара-Лапласа.
Дата добавления: 2015-02-13; просмотров: 5673;
