Примеры решения задач. Задача 1.По длинному прямолинейному цилиндрическому проводнику радиусом R течет ток силой I с постоянной плотностью внутри проводника
Задача 1.По длинному прямолинейному цилиндрическому проводнику радиусом R течет ток силой I с постоянной плотностью внутри проводника. Определите индукцию магнитного поля: а) снаружи проводника (r>R);
б) внутри проводника (r˂R).
Решение:
а) В силу симметрии индукция магнитного поля должна быть одинакова во всех точках, находящихся на одном расстоянии от центра проводника, поскольку все эти точки находятся в одинаковых физических условиях. Так как вектор 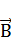 направлен по касательной к окружности, проведенной вокруг проводника, то в качестве контура интегрирования в теореме о циркуляции вектора
направлен по касательной к окружности, проведенной вокруг проводника, то в качестве контура интегрирования в теореме о циркуляции вектора 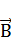 выберем окружность, описанную вокруг проводника радиусом r>R. Тогда
выберем окружность, описанную вокруг проводника радиусом r>R. Тогда
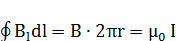 ,
,
откуда
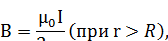
что совпадает с результатом, полученным для прямого проводника с током.
б) Внутри проводника вновь выберем контур в виде окружности с радиусом r˂R. Вектор 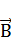 направлен по касательной к этой окружности, и в силу симметрии его величина должна быть одинаковой во всех точках контура. Охваченный контуром ток меньше полного тока I во столько же раз, во сколько площадь контура меньше площади сечения проводника: πr2/πR2. Тогда по теореме о циркуляции вектора
направлен по касательной к этой окружности, и в силу симметрии его величина должна быть одинаковой во всех точках контура. Охваченный контуром ток меньше полного тока I во столько же раз, во сколько площадь контура меньше площади сечения проводника: πr2/πR2. Тогда по теореме о циркуляции вектора 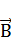
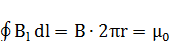 I
I 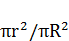
или
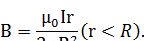
Индукция магнитного поля равна нулю в центре проводника и линейно возрастает с увеличением расстояния до центра, пока r  R; при r
R; при r 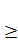 R величина В убывает как 1/r. Эти результаты справедливы для точек, близких к проводнику по сравнению с расстояниями до его концов (длинный проводник).
R величина В убывает как 1/r. Эти результаты справедливы для точек, близких к проводнику по сравнению с расстояниями до его концов (длинный проводник).
Задача 2. На деревянный тороид малого поперечного сечения намотано равномерно N витков провода, по которому течет ток I. Найти отношение η индукции магнитного поля внутри тороида к индукции в центре тороида.
Решение: Индукцию на оси тороида найдем с помощью теоремы о циркуляции 2πRB0 = µNI, где R – радиус оси тороида:
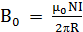 .
.
Поскольку ток подходит к тороиду и отходит от него в одной и той же точке, вдоль оси тороида также течет ток I. Таким образом индукция в центре тороида будет такой же, как от кольцевого тока радиуса R. Эту индукцию найдем с помощью закона Био-Савара-Лапласа:
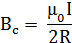
Отсюда получим искомое отношение 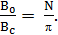
Задача 3.Докажите, пользуясь законом о циркуляции вектора 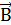 , что неоднородное магнитное поле не может иметь одно и то же направление во всем пространстве, как показано на рисунке 2.11.
, что неоднородное магнитное поле не может иметь одно и то же направление во всем пространстве, как показано на рисунке 2.11.
Решение: Линии магнитной индукции в нижней части рисунка расположены теснее, чем в верхней. Это указывает на то, что индукция магнитного поля внизу больше, чем в верхней части. В качестве замкнутого контура,
| b |
| c |
| a |
| d |
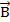
|
| Рисунок 2.11 – К задаче 3 |
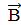 выберем прямоугольный контур abcd как показано на рисунке. Так как внутри контура тока нет, то
выберем прямоугольный контур abcd как показано на рисунке. Так как внутри контура тока нет, то 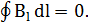
С другой стороны, используя определение циркуляции, имеем:
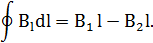
Здесь учтено, что 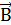 перпендикулярна dl на участках ab и cd. Последнее выражение не равно нулю, так как индукция B1 вдоль bс меньше, чем индукция B2вдоль ad. Мы пришли к противоречию. Тем самым доказано, что существование неоднородного магнитного поля, имеющего одно и то же направление, противоречит закону о циркуляции вектора
перпендикулярна dl на участках ab и cd. Последнее выражение не равно нулю, так как индукция B1 вдоль bс меньше, чем индукция B2вдоль ad. Мы пришли к противоречию. Тем самым доказано, что существование неоднородного магнитного поля, имеющего одно и то же направление, противоречит закону о циркуляции вектора 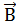 .
.
Задача 4.Плоский квадратный контур со стороной длиной а = 10 см, по которому течет ток I = 100 А, свободно установился в однородном магнитном поле индукцией В = 1 Тл. Определить работу А, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1) φ1 = 900; 2) φ2 = 30. При повороте контура сила тока в нем поддерживается неизменной.
| (1) |
М = pmBsinφ.
По условию задачи, в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю (М = 0), а значит, φ = 0, т.е векторы pmи B совпадают по направлению.
| (2) |
dA = Mdφ.
Подставив сюда выражение М по формуле (1) и учтя, что pm= IS = Ia2, где I–сила тока в контуре, S = a2–площадь контура, получим
dA = IBa2sinφdφ.
Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол:
| (3) |
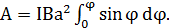
1).Работа при повороте на угол φ1 = 900
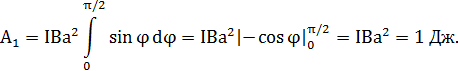
2). Работа при повороте на угол φ2 = 30. В этом случае, учитывая, что угол φ2 мал, заменим в выражении (3) 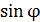 на φ:
на φ:
Задача 5.Электрон, имея скорость 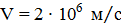 , влетел в однородное магнитное поле с индукцией
, влетел в однородное магнитное поле с индукцией 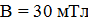 под углом
под углом 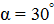 к направлению линий индукции. Определить радиус R и шаг h винтовой линии, по которой будет двигаться электрон.
к направлению линий индукции. Определить радиус R и шаг h винтовой линии, по которой будет двигаться электрон.
Решение:Известно, что на заряженную частицу, влетевшую в магнитное поле, действует сила Лоренца:
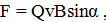 (4)
(4)
где Q – заряд частицы, в данном случае Q= 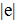
Так как вектор силы Лоренца перпендикулярен вектору скорости, то модуль скорости не будет изменяться под действием этой силы. Но при постоянной скорости, как это следует из формулы (4), останется постоянным и значение силы Лоренца. Из механики известно, что постоянная сила, перпендикулярная скорости, вызывает движение по окружности. Следовательно, электрон, влетевший в магнитное поле, будет двигаться по окружности в плоскости, перпендикулярной линиям индукции, со скоростью, равной поперечной составляющей 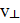 скорости (рис. 2.12); одновременно он будет двигаться и вдоль поля со скоростью
скорости (рис. 2.12); одновременно он будет двигаться и вдоль поля со скоростью 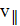 :
:
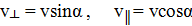
| R |
| x |
| y |
| z |
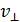
|
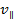
|
| α |
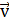
|
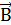
|
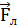
|
| O |
| h |
| Рисунок 2.12 – К задаче 5 |
Радиус окружности, по которой движется электрон, найдем следующим образом. Сила Лоренца F сообщает электрону нормальное условие ускорения 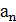 . По второму закону Ньютона,
. По второму закону Ньютона, 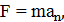 , где
, где 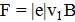 , и
, и 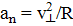 . Тогда
. Тогда
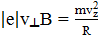 ,
,
отсюда после сокращения на 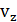 находим радиус винтовой линии:
находим радиус винтовой линии:
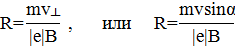
Подставив значение величин m, v, e, B и α и произведя вычисления, получим
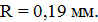
Шаг винтовой линии равен пути, пройденному электроном вдоль поля со скоростью 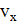 за время, которое понадобится электрону для того, чтобы совершить один оборот,
за время, которое понадобится электрону для того, чтобы совершить один оборот,
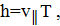 (5)
(5)
где 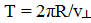 - период вращения электрона. Подставив это выражение для T в формулу (5), найдем:
- период вращения электрона. Подставив это выражение для T в формулу (5), найдем:
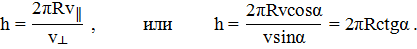
Подставив в эту формулу значения величин 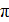 , R и
, R и 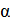 , получим
, получим
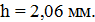
Задача 5.Электрон движется в однородном магнитном поле с индукцией В = 0,03 Тл по окружности радиусом r = 10 см. Определить скорость v электрона.
Решение: Движение электрона по окружности в однородном магнитном поле совершается под действием силы Лоренца. Поэтому можно написать
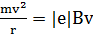 ,
,
откуда найдем импульс электрона:
p = mv = |e|Br.
Релятивистский импульс выражается формулой
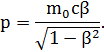
Выполнив преобразования, получим следующую формулу для определения скорости частицы:
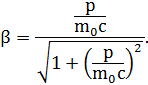
В данном случае p = |e|Br. Следовательно,
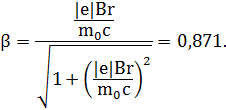
Или
v = cβ = 2,61∙108м\с.
Электрон, обладающий такой скоростью, является релятивистским.
Вывод: Если скорости частиц достигают значений, соизмеримых со скоростью света в вакууме, то следует учитывать релятивистский эффект возрастания массы со скоростью и неприменимость формул классической механики Ньютона.
Контрольные вопросы второго уровня (сборник задач)
1. Проводник длиной 110 см согнули под углом 60° так, что одна из сторон угла равна 30 см, и поместили в однородное магнитное поле с индукцией 2 мТл обеими сторонами перпендикулярно линиям индукции. Какая сила будет действовать на этот проводник, если по нему пропустить ток силой 10 А? [17 мН]
2. Прямой проводник, расположенный перпендикулярно линиям магнитной индукции, при пропускании по нему тока силой 1 А приобрел ускорение 2 м/с2. Площадь поперечного сечения проводника 1 мм2, плотность материала проводника 2500 кг/м3. Чему равна индукция магнитного поля? Силу тяжести не учитывать. [5 мТл]
3. Проводник длиной 10 см располагается горизонтально в однородном магнитном поле с индукцией 1 мТл так, что сила тяжести уравновешивается магнитной силой. Напряжение на концах проводника 100 В, его удельное сопротивление 105 Ом∙м. Чему равна плотность материала этого проводника? [104 кг/м3]
4. Стержень массой 20 г и длиной 5 см положили горизонтально на гладкую наклонную плоскость, составляющую с горизонтом угол, тангенс которого равен 0,3. Вся система находится в вертикальном магнитном поле с индукцией 150 мТл. При какой силе тока в стержне он будет находиться в равновесии? [8 А]
5. Три стороны квадрата из проволоки жестко скреплены друг с другом, а четвертая может скользить по ним. Квадрат расположен на горизонтальной поверхности и находится в однородном вертикальном магнитном поле с индукцией 100 мТл. Какой ток надо пропустить по контуру, чтобы сдвинуть подвижную сторону, если ее масса 20 г, а коэффициент трения в контактах 0,2? Сторона квадрата 10 см. [4 А]
6. Проволочная квадратная рамка массой 10 г со стороной 10 см может вращаться вокруг горизонтальной оси, совпадающей с одной из ее сторон. Рамка находится в однородном вертикальном магнитном поле с индукцией 0,1 Тл. При какой минимальной силе тока в рамке она будет неподвижна и наклонена к горизонту под углом 45°? [10 А]
7. Прямоугольный контур площадью 150 см2 с током силой 3 А, на который действует только однородное магнитное поле с индукцией 0,1 Тл, занял положение устойчивого равновесия. Какую после этого надо совершить работу, чтобы медленно повернуть его на 180° вокруг оси, проходящей через середины противоположных сторон? [9 мДж]
8. На два жестких параллельных проводника, расположенных горизонтально на расстоянии dдруг от друга, уложен, как на рельсы, перпендикулярно им легкий металлический стержень массой m. Эта система находится в однородном магнитном поле с индукцией В, направленном вертикально вверх. В момент t = 0 проводники - рельсы подключаются к источнику постоянного напряжения, и через систему течет ток I. Определите скорость стержня как функцию времени, считая коэффициент трения равным μ. [ 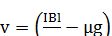 ]
]
9. По криволинейному проводнику, соединяющему точки а и b, в плоскости, перпендикулярной однородному магнитному полю с индукцией В, течет ток I. Покажите, что сила, действующая со стороны магнитного поля на проводник, не зависит от его формы и равна силе, действующей на прямолинейный проводник, соединяющий точки аи b, по которому течет ток такой же силы I.
10. Проводник в виде тонкого полукольца радиусом R = 10 см находится в однородном магнитном поле с индукцией В= 50 мТл. По проводнику течет ток I =10 А. Найдите силу, действующую на проводник, если плоскость полукольца перпендикулярна линиям индукции, а подводящие ток провода находятся вне поля. [0,1 Н]
11. По тонкому проводнику в виде кольца радиусом R = 20 см течет ток. Перпендикулярно плоскости кольца возбуждено однородное магнитное поле с индукцией В = 20 мТл. Сила, растягивающая кольцо, равна 0,4 Н. Определите силу тока в кольце. [100 А]
12. По двум тонким проводникам, изогнутым в виде кольца радиусом R= 20 см, текут одинаковые токи по 100 А каждый. Найдите силу взаимодействия этих колец, если плоскости, в которых лежат кольца, параллельны, а расстояние между центрами колец d= 2 мм. [1,26 Н]
13. Перпендикулярно магнитному полю возбуждено электрическое поле напряженностью 100 кВ/м. Перпендикулярно обоим полям движется заряженная частица с постоянной скоростью 100 км/с. Чему равна индукция магнитного поля? [1 Тл]
14. Протон влетает со скоростью 60 км/с в пространство с электрическим и магнитным полями, силовые линии которых совпадают по направлению, перпендикулярно к этим линиям. Определите напряженность электрического поля, если индукция магнитного поля 0,1 Тл, а начальное ускорение протона, вызванное действием этих полей, равно 1012 м/с2. Отношение заряда протона к его массе 108 Кл/кг. [8 кВ/м]
15. Сила, действующая на электрон в магнитном поле максимальна, когда он движется в западном направлении. Сила направлена вверх и равна 1,04- 10-13 Н при скорости электрона 8,7∙103 м/с. Определите величину и направление вектора магнитной индукции В. [0,75 Тл]
16. На электрон, движущийся в магнитном поле В = 0,72  Тл, действует сила
Тл, действует сила 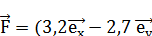 )∙10-13 Н. Чему равна скорость электрона? [
)∙10-13 Н. Чему равна скорость электрона? [ 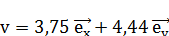 ]
]
17. Протон и альфа-частица влетают в однородное магнитное поле перпендикулярно силовым линиям поля. Во сколько раз период обращения альфа-частицы больше периода обращения протона? [В 2 раза]
18. Электронно-лучевую трубку с отключенной управляющей системой помещают в однородное магнитное поле, перпендикулярное скорости движения электронов. При этом след пучка электронов на экране, удаленном на 14 см от места вылета электронов, смещается на 2 см. Какова скорость электронов, если индукция магнитного поля 25 мкТл? [627 км/с]
19. Чему равна скорость пучка электронов, который не испытывает отклонения в скрещенных электрическом (8,8∙103 В/м) и магнитном (3,5∙10 3 Тл) полях? По окружности какого радиуса будут двигаться электроны, если снять электрическое поле? [2,5∙106 м/с; 4 мм]
20. Протон в магнитном поле с индукцией 0,01 Тл движется по дуге окружности радиусом 1 м. После вылета из магнитного поля он полностью тормозится электрическим полем. Чему равна тормозящая разность потенциалов? [4,8 кВ]
21. Отрицательно заряженная частица влетает в область однородного магнитного поля с индукцией 0,001 Тл, где движется по окружности радиусом 0,2 м. Затем частица попадает в однородное электрическое поле, где пролетает участок с разностью потенциалов 1000 В, при этом ее скорость уменьшается в 3 раза. Определите конечную скорость частицы. [3,75 106 м/с]
22. Грузик массой 2 г с зарядом 4 мКл, подвешенный на невесомой нити, находится в вертикальном магнитном поле с индукцией 3 Тл. Грузик дважды приводят во вращение в горизонтальной плоскости, причем радиусы вращения в обоих случаях одинаковы, а направления вращения противоположны. На сколько отличаются угловые скорости этих вращательных движений? [На 6 рад/с]
23. Заряженная частица движется по окружности радиусом R= 1 см в однородном магнитном поле. Параллельно магнитному полю возбуждено электрическое поле напряженностью E=100 В/м. Вычислите индукцию магнитного поля, если за время 10 мкс, в течение которого действовало электрическое поле, кинетическая энергия частицы возросла вдвое. [0,1 Тл]
24. Электрон движется в однородном магнитном поле с индукцией В=9 мТл по винтовой линии, радиус которой r= 1 см и шаг h = 7,8 см. Определите период обращения электрона и его скорость. [3,9∙10-9 с, 2,56∙10-7 м/с]
25. В однородном магнитном поле движется протон. Траектория его движения представляет собой винтовую линию с радиусом R = 10 см и шагом h = 60 см, кинетическая энергия протона 580 фДж. Чему равна величина индукции магнитного поля? [2 Тл]
26. Определите циркуляцию вектора магнитной индукции по окружности, через центр которой перпендикулярно ее плоскости проходит бесконечно длинный прямолинейный провод, по которому течет ток I = 5 А. [6,28 мкТл∙м]
27. По соленоиду длиной l = 1 м без сердечника, имеющему N = 103 витков, течет ток I = 20 А. Определить циркуляцию вектора магнитной индукции вдоль контура, изображенного на рисунке 2.13 аи б. []
| a |
| b |
| а |
| б |
| Рисунок 2.13 – К задаче 27 |
| a |
| b |
28. Вычислить циркуляцию вектора индукции вдоль контура, охватывающего токи I1 = 10 А, I2 = 15 А, текущие в одном направлении, и ток I3 = 20 А, текущий в противоположном направлении. []
29. По сечению проводника равномерно распределен ток плотностью 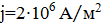 . Найти циркуляцию вектора напряженности вдоль окружности радиусом
. Найти циркуляцию вектора напряженности вдоль окружности радиусом 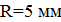 , проходящей внутри проводника и ориентированной так что ее плоскость составляет угол
, проходящей внутри проводника и ориентированной так что ее плоскость составляет угол 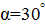 с вектором плотности тока. []
с вектором плотности тока. []
30. L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA1bF5qsQA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBCF7wX/wzKCt7qJQiupq4igeCiURr1Ps9Mk NTsbsmtM/n3nUOhthvfmvW/W28E1qqcu1J4NpPMEFHHhbc2lgcv58LwCFSKyxcYzGRgpwHYzeVpj Zv2DP6nPY6kkhEOGBqoY20zrUFTkMMx9Syzat+8cRlm7UtsOHxLuGr1IkhftsGZpqLClfUXFLb87 A/1P/l5fx6/08nq094+41Mdx7I2ZTYfdG6hIQ/w3/12frOCnQivPyAR68wsAAP//AwBQSwECLQAU AAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnht bFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVs c1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4 bWwueG1sUEsBAi0AFAAGAAgAAAAhANWxearEAAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9k b3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACJAwAAAAA= " fillcolor="white [3212]" strokecolor="black [3213]" strokeweight="1pt"/>
| D |
| O |
| Рисунок 2.14 – К задаче 30 |
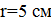 . По обмотке тороида, содержащей N = 2000 витков, течет ток
. По обмотке тороида, содержащей N = 2000 витков, течет ток 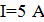 (рис. 2.14). Пользуясь законом полного тока, определить максимальное и минимальное значение магнитной индукции B в тороиде. []
(рис. 2.14). Пользуясь законом полного тока, определить максимальное и минимальное значение магнитной индукции B в тороиде. []
Контрольные вопросы третьего уровня (тесты)
| 1. На рисунке указаны траектории заряженных частиц, имеющих одинаковую скорость и влетающих в однородное магнитное поле, перпендикулярное плоскости чертежа. Если заряд частицы отрицателен, то ее траектория соответствует номеру ... | 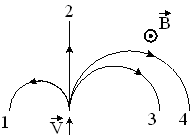
| |||||||||
| 1. | 2. | 3 и 4 | 3. | |||||||
| 2. На рисунке указаны траектории заряженных частиц, имеющих одинаковую скорость и влетающих в однородное магнитное поле, перпендикулярное плоскости чертежа. Если заряд частицы положителен, то ее траектория соответствует номеру .. | 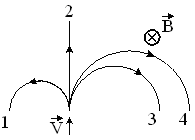
| |||||||||
| 1. | 3 и 4 | 2. | 3. | |||||||
| 3. Пучок однократно ионизированных изотопов магния 24Mg и 25Mg,движущихся с одинаковой скоростью, влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции. Радиусыокружностей, по которым движутся ионы, связаны соотношением ... | 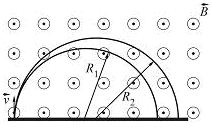
| |||||||||
| 1. | 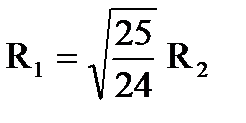
| 2. | 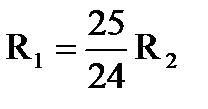
| |||||||
| 3. | 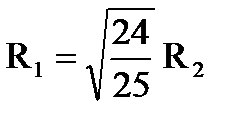
| 4. | 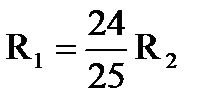
| |||||||
4. Ионы, имеющие одинаковые удельные заряды влетают в однородное магнитное поле. Их траектории приведены на рисунке.
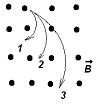
Наименьшую скорость имеет ион, движущийся по траектории…
1. характеристики траекторий не зависят от скорости 2.3 3.2 4. 1
5.Какая формула определяет силу Лоренца?
1. 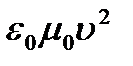 2.
2. 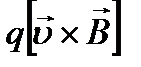 3.
3. 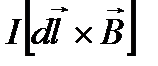 4.
4. 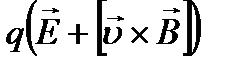 5.
5. 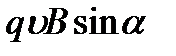
6. Какая формула определяет поле тороида?
1. 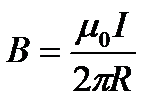 2.
2. 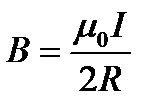 3.
3. 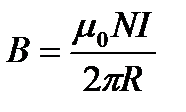 4.
4. 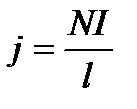 5.
5. 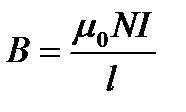
7. Какая формула определяет поле соленоида?
1. 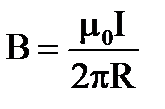 2.
2. 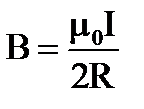 3.
3. 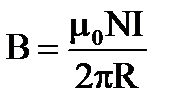 4.
4. 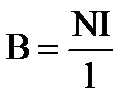 5.
5. 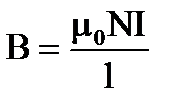
8. Чему равна частота обращения частицы с зарядом е и массой m, влетающей со скоростью V перпендикулярно линиям индукции В в магнитное поле?
1. 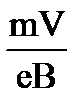 2.
2. 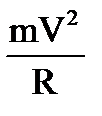 3.
3. 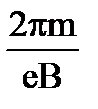 4.
4. 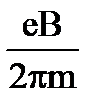 5.
5. 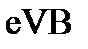
9. В каком случае заряженная частица будет двигаться по спирали в однородном магнитном поле?
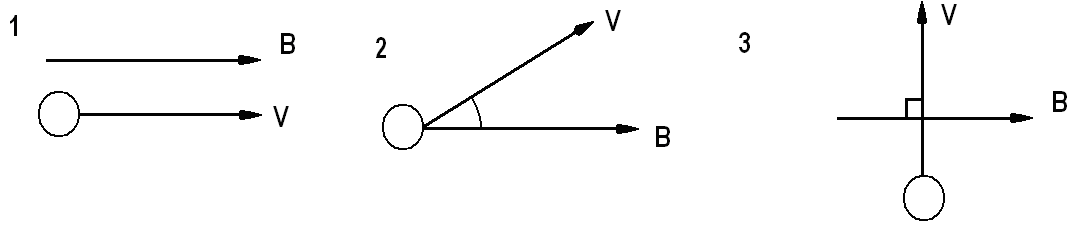
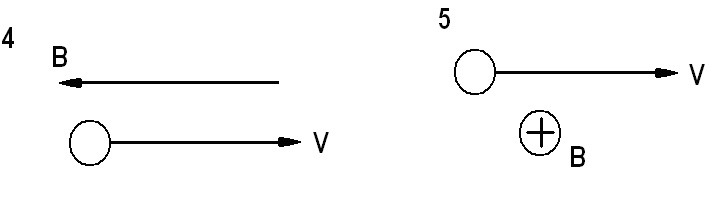
10. Чему равен радиус окружности частицы с зарядом е и массой m, влетающей со скоростью V перпендикулярно линиям индукции В в магнитное поле?
1. 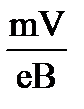 2.
2. 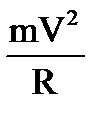 3.
3. 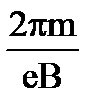 4.
4. 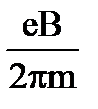 5.
5. 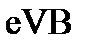
11. Формула, определяющая циркуляцию индукции для произвольного распределения тока в пространстве:
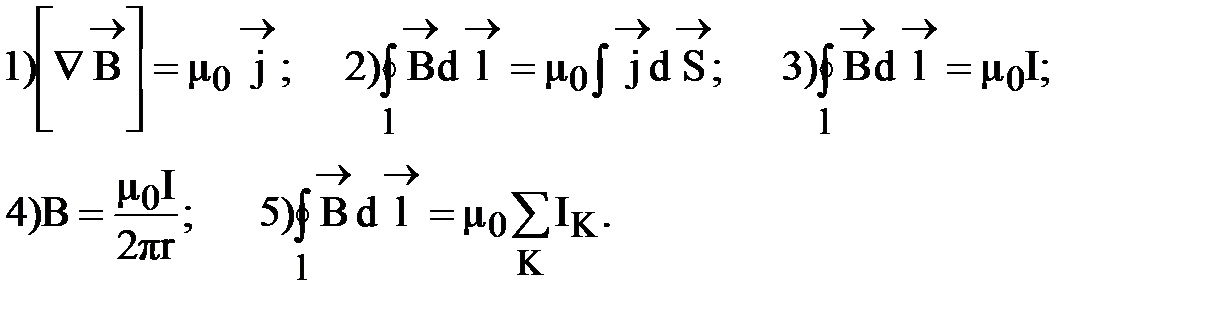
Дата добавления: 2015-02-13; просмотров: 12091;
