Метод искусственного базиса (М-метод). Описанный процесс решения ЗЛП симплекс-методом довольно трудоемкий и требует выполнения однообразных преобразований

Описанный процесс решения ЗЛП симплекс-методом довольно трудоемкий и требует выполнения однообразных преобразований. Причем с возрастанием числа неизвестных растет и число шагов.

Оказывается, эти преобразования можно записать в виде последовательности однотипно заполненных таблиц, называемых симплекс-таблицами.

Изложим способ составления и преобразования таких таблиц на примерах первой и второй основных задач .

I. Первая основная задача.

Для заполнения первой симплекс-таблицы необходимо переписать целевую функцию F и систему ограничений в виде:

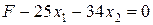
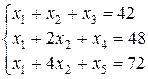
Заполним таблицу

Базисные неизвестные	Свободные члены
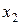
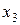
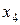
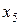
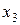
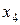
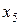
F		–25	–34

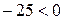В выражении для F выясняем, имеются ли в последней строке таблицы, кроме столбца «свободные члены», отрицательные числа. Если таковых нет, то задача решена. Если же есть, то выполняем преобразование: в столбце имеем (из двух отрицательных чисел –25 и –34 выбирают меньшее по модулю), над этим элементом ищем положительные числа. Если таковых нет, то задача не имеет решения. В нашем случае над –25 есть три положительных числа: 1; 1 и 1.

Найдем

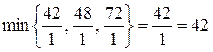
Элемент, стоящий на пересечении строки ( 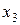) и столбца ( ), называем разрешающим. В нашем случае он равен 1. (Если разрешающий элемент равен числу 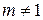, то всю строку делят на разрешающий элемент m, чтобы получить 1). Неизвестная вводится в базис, а неизвестная 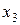выводится из него.

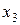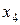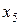Заполняем вторую симплекс-таблицу. Строка ( ) из первой таблицы становится в ней строкой ( ). Далее преобразуем строки ( ), ( ) и (F) первой таблицы так, чтобы их элементы, стоящие в столбце ( ), обратились в 0. С этой целью

1) вычтем элементы строки ( ) из соответствующих элементов строки ( 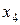), и запишем полученные результаты в строку ( 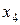) второй таблицы;

2) вычтем элементы строки ( ) из соответствующих элементов строки ( 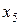), и запишем полученные результаты в строку ( 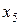) второй таблицы;

3) умножим элементы строки ( ) на 25, сложим с соответствующими элементами строки (F), и запишем полученные результаты в строку (F) второй таблицы.

В результате получим следующую симплекс-таблицу

Базисные неизвестные	Свободные члены
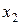
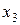
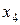
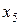
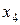
				–1
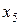
				–1
F			–9

В строке (F) есть отрицательное число –9. Поэтому продолжим поиск оптимального решения. Над –9 есть три положительных числа: 1; 1 и 3.

Найдем

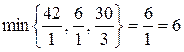
Элемент, стоящий на пересечении строки ( 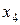) и столбца ( 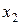) разрешающий и равен 1. Неизвестная 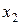вводится в базис, а неизвестная 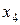выводится из него.

Заполняем третью симплекс-таблицу. Строка ( 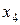) из второй таблицы становится в ней строкой ( 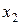). Далее преобразуем строки ( ), ( ) 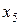и (F) второй таблицы так, чтобы их элементы, стоящие в столбце ( 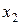), обратились в 0. С этой целью

1) вычтем элементы строки ( 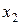) из соответствующих элементов строки ( ), и запишем полученные результаты в строку ( ) третьей таблицы;

2) умножим элементы строки ( 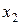) на 3, вычтем из соответствующих элементов строки ( 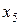), и запишем полученные результаты в строку ( 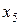) третьей таблицы;

3) умножим элементы строки ( 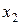) на 9, сложим с соответствующими элементами строки (F), и запишем полученные результаты в строку (F) третьей таблицы.

В результате получим следующую симплекс-таблицу

Базисные неизвестные	Свободные члены
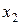
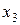
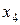
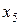
					–1
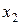
				–1
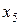
					–3
F

В строке (F) нет отрицательных чисел. Получили оптимальное решение:

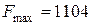
при , , , .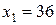

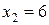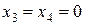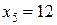Замечание. Симплекс-таблицы удобнее «пристыковывать» друг к другу по вертикали, что позволяет не писать многократно заглавную строку

II. Вторая основная задача.

Для заполнения первой симплекс-таблицы перепишем целевую функцию F и систему ограничений (6.14), имеющую допустимый вид, следующим образом:

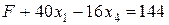
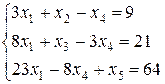
Заполним таблицу

Базисные неизвестные	Свободные члены
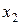
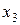
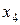
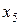
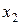
					–1
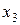
					–3
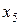
					–8
F					–16
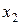
	1,125			–0,375	0,125
	2,625			0,125	–0,375
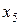
	3,625			–2,875	0,625
F				–5	–1

В выражении для F выясняем, имеются ли в последней строке таблицы, кроме столбца «свободные члены», положительные числа. Если таковых нет, то задача решена. Если же есть, то выполняем преобразование: в столбце имеем . Над этим элементом ищем положительные числа. Если таковых нет, то задача не имеет решения. В нашем случае над 40 есть три положительных числа: 3; 8 и 23.

Найдем

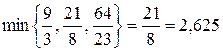
Элемент, стоящий на пересечении строки ( 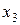) и столбца ( ) разрешающий и равен 8. Неизвестная вводится в базис, а неизвестная 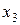выводится из него. Все элементы строки ( 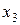) разделим на разрешающий элемент. Полученные результаты запишем в новую симплекс-таблицу в строке ( ).

Преобразуем строки ( 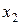), ( ) 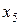и (F) первой таблицы так, чтобы их элементы, стоящие в столбце ( ), обратились в 0. С этой целью

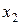1) умножим элементы строки ( ) на 3, вычтем из соответствующих элементов строки ( ), и запишем полученные результаты в строку ( ) второй таблицы;

2) умножим элементы строки ( ) на 23, вычтем из соответствующих элементов строки ( 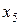), и запишем полученные результаты в строку ( 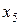) второй таблицы;

3) умножим элементы строки ( ) на 40, вычтем из соответствующих элементов строки (F), и запишем полученные результаты в строку (F) второй таблицы.

В строке (F) нет положительных чисел. Получили оптимальное решение: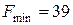

при , , , .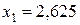

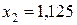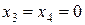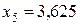Замечание. Первая симплекс-таблица второй основной задачи была заполнена с учетом того, что система ограничений (6.11) была предварительно сведена к допустимому виду (6.14), т.е. был найден допустимый базис. Зачастую поиск такого базиса довольно затруднителен. Рассмотрим следующий метод нахождения допустимого базиса, который называют методом искусственного базиса или М-методом.