Определения. Опред.:Обыкновенным дифференциальным уравнением -ного порядка называется уравнение , где - независимая переменная

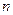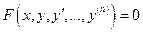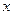Опред.:Обыкновенным дифференциальным уравнением -ного порядка называется уравнение , где - независимая переменная, 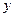- искомая функция от 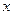, 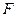- заданная функция от 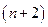переменных.

Опред.:Функция 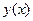называется решением дифференциального уравнения на интервале 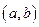, если при подстановке в это уравнение она обращает его в тождество по 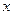, на интервале .

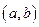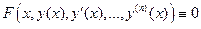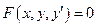, - дифференциальное уравнение 1-го порядка.

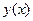- решение ДУ 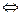интеграл ДУ

Опред.:Интегральная кривая ДУ - график любого решения ДУ.

Опред.: Интегрирование в квадратурах - выражение решения дифференциального уравнения с помощью элементарных функций и интегралов от них.

,

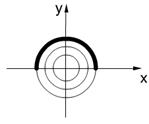
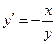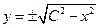
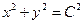(неявная функция, решение ДУ)

Опред.: Интегральная кривая – полуокр. (верхняя или нижняя)

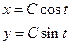
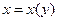
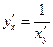
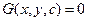(общий интеграл ДУ)

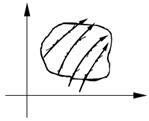3°. Геометрический смысл ДУ.

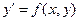(это ДУ, разрешенное относительно производной)

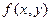- определена в области .

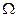В каждой точке области мы знаем касательную к решению.

Опред.: Совокупность линий называют полем направлений, соответствующим дифференциальному уравнению.

С геометрической точки зрения нахождение решений ДУ- есть нахождение всех кривых, касательные в каждой точке к которым совпадают с соответствующими прямыми поля направлений.