Динамика численности популяций с непрерывным размножением. Логистическое уравнение

До сих пор мы рассматривали модели, применимые к популяциям с дискретными периодами размножения. Но в природе встречаются и популяции, где рождение и гибель организмов происходит непрерывно; для таких популяций модели, выраженные предыдущими уравнениями непригодны.

Рассмотрим популяцию с непрерывным размножением и построим модель изменения ее численности N. Математическим аппаратом здесь являются дифференциальные уравнения. Скорость роста численности в этом случае можно обозначить 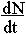,тогда средняя скорость увеличения численности в расчете на одну особь определяется величиной .

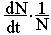
Без учета внутривидовой конкуренции получаем

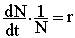или

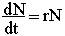(1)

Через rобозначено приращение численности за единицу времени в пересчете на одну особь. Понятно, что численность популяции при r > 0 будет неограниченно возрастать, т.е. будет наблюдаться экспоненциальный рост.

Теперь попробуем учесть внутривидовую конкуренцию. Для этого воспользуемся методом, который однажды уже применяли (см. рис. 1).

Обратимся к рис. 5. Когда численность популяции близка к нулю, скорость роста определяется величиной r , так как конкуренция еще не оказывает влияния на прирост популяции (точка А). Когда же при возрастании N достигается значение К (предельной плотности насыщения), скорость роста популяции снижается до нуля (точка В).

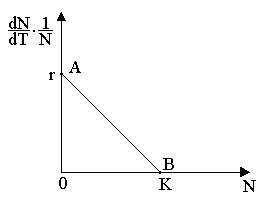Рис.5. Зависимость скорости воспроизводства от численности популяции.

Записав уравнение прямой АВ, получим

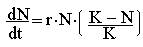(2)

Последнее уравнение известно под названием «логистического». Одно из его достоинств – простота. Уравнение относится к ОДУ и допускает аналитическое решение:

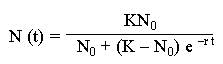(3)

В истории экологии логистическое уравнение сыграло значительную роль, оказав большое влияние на применение в экологии математических методов. С другой стороны, простота уравнения накладывает ограничения на область его применения, так как с его помощью можно описать немногие реальные популяции. Но, несмотря на все ограничения, логистическое уравнение используется как составная часть в других моделях динамики численности популяций, рассматриваемых ниже.

Изменение численности популяции в соответствии с формулами (2)–(3) иллюстрирует рис.6.

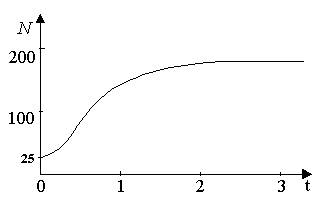Рис. 6. Динамика численности популяции при N₀ = 25, К = 200, r = 3.