Логистическая модель межвидовой конкуренции.

Сущность межвидовой конкуренции заключается в том, что у особей одного вида уменьшается плодовитость, выживаемость и скорость роста в результате использования того же ресурса, что и особями другого вида, причем влиянию конкуренции в той или иной мере подвергаются особи обоих видов.

Для двух различных популяций введем соответствующие обозначения:

Пусть N₁, N₂ — численности первой и второй популяций.

К₁, К₂ – предельные плотности насыщения первой и второй популяций.

г₁и r₂ – максимальные врожденные скорости роста первой и второй популяций.

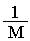Обратимся к логистическому уравнению (2) и попробуем учесть в нем межвидовую конкуренцию. Сделаем это так. Предположим, что Мособей вида 2 оказывают такое же воздействие на вид 1, как одна особь вида 1. Константу в этом случае называют коэффициентом конкуренции.

Обозначим ее a₁₂.Таким образом, чтобы отразить суммарное воздействие на вид 1, надо в логистическом уравнении (2) в числителе дроби вместо N записать 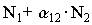. Аналогично получается уравнение для исследования численности второй популяции. В результате получаем систему двух дифференциальных уравнений:

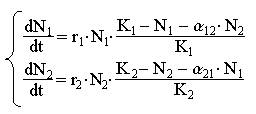
(4)

Модель межвидовой конкуренции, выраженная этой системой, названа в честь ее авторов «моделью Лотки–Вольтерры».

Заметим, что если коэффициенты a₁₂или a₂₁ больше единицы, то влияние со стороны конкурирующей популяции на особей данного вида сильнее, чем со стороны особей своего вида.

Изобразим графически динамику численности двух популяций при следующих данных: r₁= 2, r₂=4, К₁=200, К₂=180, a₁₂=0,5, a₂₁=0,65, N₁⁽⁰⁾=100, N₂⁽⁰⁾=25.

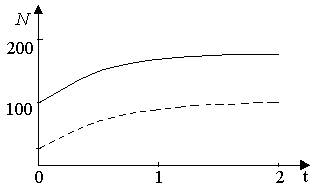
Рис.7. Устойчивое сосуществование популяций при r₁= 2, r₂=4, К₁=200, К₂=180, a₁₂=0,5, a₂₁=0,65, N₁⁽⁰⁾=100, N₂⁽⁰⁾=25. Устойчивое сосуществование достигается лишь при а₁₂ • а₂₁ < 1. Сплошная линия – численность первой популяции, штриховая – второй.

Главный вопрос, который интересует исследователя межвидовой конкуренции – при каких условиях увеличивается или уменьшается численность каждого вида? Для ответа на этот вопрос надо построить фазовую плоскость, где были бы изображены все возможные сочетания численностей N₁, N₂. На таких диаграммах численность одного вида, например, N₁ откладывают по горизонтальной оси, а другого – по вертикальной. При одних сочетаниях численностей N₁, N₂ будет отмечаться рост выбранной для наблюдения популяции, при других – уменьшение ее численности. Также для каждого из видов можно провести изоклины – линии, вдоль которых не наблюдается ни увеличения, ни уменьшения численности (численность постоянна).

Рассмотрим, как можно построить изоклину на фазовой плоскости для первого

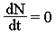вида. По определению, для этой линии . . Из первого уравнения системы (4) получаем

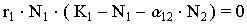
Это равенство выполняется, если какой-либо из множителей равен нулю. Наибольший интерес представляет ситуация, в которой

,

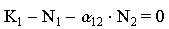получим уравнение изоклины для вида 1:

.

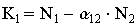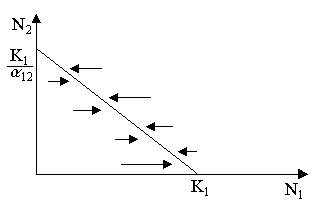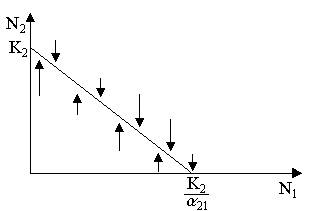
Рис. 8. Изоклины, полученные с помощью модели Лотки-Вольтерры. Длины стрелок пропорциональны изменению численности, стрелки указывают направление изменения численности

Таким образом, получено уравнение изоклины, которое, как можно заметить, является уравнением прямой в плоскости (N₁, N₂). Вверх и вправо от изоклины из-за высокой численности обеих популяций численность вида 1 снижается, в противоположных направлениях – повышается. Аналогично можно построить изоклину для вида 2. На рис. 8 построены соответствующие изоклины, и показано изменение численности популяций.

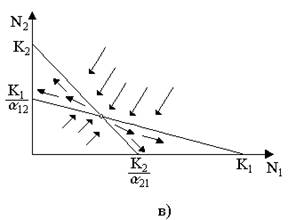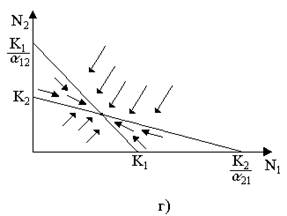
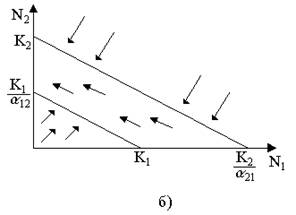
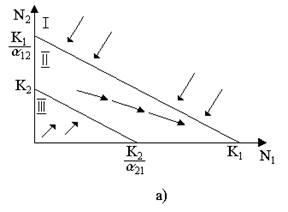
Рис.9. Результаты конкуренции, полученные с помощью модели Лотки-Вольтерры при различных параметрах. На рисунке а в зоне I численность обеих популяций падает; в зоне II – численность первой популяции растет, второй уменьшается; в зоне III -численность обеих популяций увеличивается.

Для решения поставленной выше задачи объединим и одной фазовой плоскости изоклины для обоих видов и будем одновременно исследовать динамику их численности. Изоклины относительно друг друга располагаются четырьмя различными способами, что дает различный исход конкуренции. Пи рис.9 представлены результаты конкуренции, полученные с помощью системы уравнений (4), заимствованные из книги М. Бигона и др. «Экология».