Модели внутривидовой конкуренции.

Рассмотрим простейшую из указанных моделей для вида с дискретными периодами размножения, в которой численность популяции в момент времени t равна N_t и изменяется во времени пропорционально величине основной скорости воспроизводства R. К таким видам относятся, например, большая часть растений, некоторые виды насекомых, у которых разные поколения четко разнесены во времени. Коэффициент R характеризует количество особей, которое воспроизводится в расчете на одну существующую. Данная модель может быть выражена уравнением геометрической прогрессии

N_t+1= N_t * R; (1)

решение, которого имеет вид:

N_t=N₀*R^t; (2)

гдe N₀- начальная численность популяции. Эта модель, однако, oписывает популяцию, в которой отсутствует конкуренция и в которой R является константой. Если R>1, то численность популяции будет бесконечно увеличиваться. В реальности работают механизмы сдерживания роста популяции. В литературе приводится немало интересных примеров быстрого роста численности популяций, если бы для их размножения существовали идеальные условия. Особенно это относится к насекомым, растениям и микроорганизмам, которые могли бы покрыть земной шар толстым слоем, если им создать благоприятные условия для размножения. Но в действительности такого роста популяций, когда их численность увеличивается в геометрической прогрессии, на сколько-нибудь длительных промежутках времени не наблюдается.

Следовательно, в первую очередь необходимо изменить уравнение (1) таким образом, чтобы чистая скорость воспроизводства зависела oт внутривидовой конкуренции.

Конкуренцию можно определить как использование некоего ресурса (пиши, воды, света, пространства) каким-либо организмом, который тем самым уменьшает доступность этого ресурса для других организмов. Если конкурирующие организмы, принадлежат к одному виду, то взаимоотношения между ними называют внутривидовой конкуренцией, если же они относятся к разным видам, то отношения называют межвидовой конкуренцией.

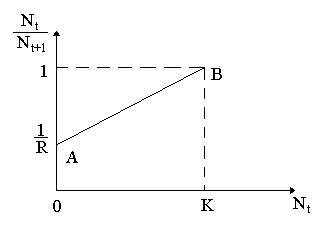
Рис. 1. К вопросу oб ограничении скорости роста популяции.

Изменим уравнение (1)в зависимости от внутривидовой конкуренции. На рис.1. показана возможная простейшая зависимость скорости воспроизводства от численности популяции N_t. Точка А отражает ситуацию, в которой численность популяции близка к нулю, конкуренция при этом практически отсутствует, и фактическую скорость воспроизводства вполне можно описывать параметром R в его первоначальном виде. Следовательно, при низкой плотности популяции уравнение (1) вполне справедливо. В преобразованном виде оно выглядит так:

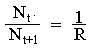(3)

Точка В,напротив, отражает ситуацию, в которой численность популяции высока, и в значительной степени проявляется внутривидовая конкуренция. Фактическая скорость воспроизводства в результате конкуренции настолько снижена, что популяция в целом может не более чем восстанавливать в каждом поколении свою численность, потому что количество родившихся особей уравновешивается количеством погибших. Этой гипотезе, отраженной на рис.1, соответствует уравнение:

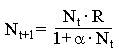(4)

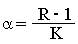где

Это уравнение является моделью роста популяции, ограниченного внутривидовой конкуренцией. Суть этой модели в том, что константа R в уравнении (1) заменена на фактическую скорость воспроизводства, т.е. R/(1 + a N_t)которая уменьшается по мере роста численности популяции N_t. Достоинство полученного уравнения заключается в его простоте. Такой тип конкуренции приводит к саморегуляции численности популяции, изображенной на рис. 2 (для некоторого набора параметров модели; численное решение).

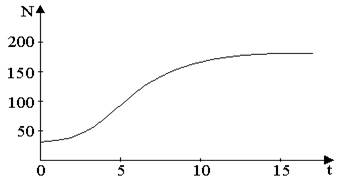
Рис. 2.Изменение численности популяции согласно уравнению (4) при R=2, К=200, N₀=20

Далее может быть получена гораздо более общая модель, учитывающая интенсивность конкуренции. Простейшая из возможных зависимостей падения скорости роста популяции от ее численности, изображенная на рис.1, является не законом природы, а всего лишь удобной гипотезой. Далеко не всегда реальная динамика численности популяции, определяемая внутривидовой конкуренцией, даже качественно согласуется с изображенной на рис.2. Более общая гипотеза о законе падения скорости роста популяции в зависимости oт ее численности приводит к следующему уравнению:

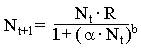(5)

В отличие от уравнения (4) модель (5) более общая, т. к. в нее введен параметр b, который определяет тип зависимости падения скорости роста популяции от ее численности.

Набор величин α, b, R можно использовать для сравнения и противопоставления сильно различающихся ситуаций. Другим положительным качеством уравнения (5) является его способность освещать новые стороны реального мира. Путем анализа кривых динамики популяций, полученных с помощью уравнения, можно прийти к предварительным выводам относительно динамики природных популяций.

На рис. 3, а, б, построенных с помощью численного моделирования, показаны различные варианты динамики численности популяции, полученные с помощью уравнения (5) при разном сочетании параметров b и R.

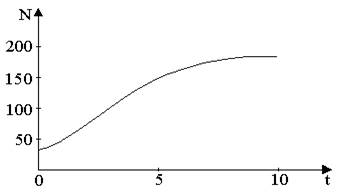
Рис.3, а. Монотонное установление стационарной численности

популяции при b = 1.4 , R = 2

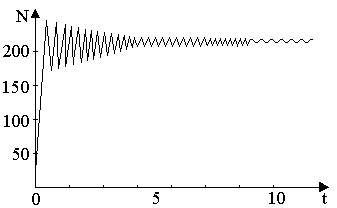
Рис.3, б. Колебательное установление стационарной численности популяции при b=3.9, R=2.

Исследования модели (5) приводят к построению на фазовой плоскости (b, R) границ, которые разделяют монотонное затухание, затухающие колебания, устойчивые предельные циклы и случайные (хаотические) изменения (Рис.4). Для этого надо задаться значениями α и N₀ и производить расчеты, изменяя параметры b, R. Различить каждый из возможных режимов можно попытаться визуально, выполняя построение на экране компьютера графиков изменения численности популяции и запоминая соответствующие значения параметров b, R при переходе от одного режима к другому. Следует, однако, понимать, что установление различий между квазипериодическими, апериодическими и хаотическими движениями – сложная математическая задача. Для ее решения используются методы преобразований Фурье и другие, рассмотрение которых выходит за пределы данного курса.

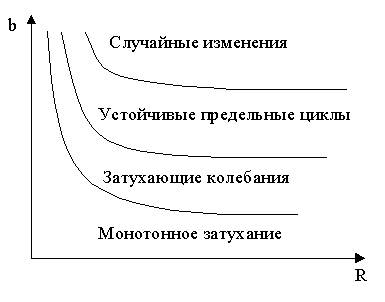
Рис.4. Схематическое изображение фазовой диаграммы динамики численности популяции с дискретным размножением.