Волновое уравнение
Когда мы рассматриваем процессы, связанные с распространением света в волокне, по соображениям удобства или наглядности мы иногда применяем лучевую теорию, считая свет потоком частиц, а иногда рассматриваем волновую природу света. Односторонний подход приводит к ошибочным результатам, поскольку свет имеет дуалистическую природу, обладая как свойствами волны, так и частицы. Распространение электромагнитных волн в волокне подчиняется уравнениям Максвелла, которые в данном случае имеют вид:
rot H = ε 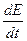 (5.1) и rot E = - μ
(5.1) и rot E = - μ 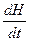 (5.2).
(5.2).
Если волна гармоническая, то есть E = Em ejωt и H = Hm ejωt, то уравнения принимают вид
rot H = jωεE (5.3) и rot E = - jωμH (5.4).
Применим ещё раз операцию взятия ротора от левой и правой части уравнения (5.4). Получим
rot rot E = -jωμ rot H. (5.5).
Из векторного анализа известно, что
rot rot E = grad div E - 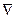 2E.
2E.
В оптическом волокне div E = 0, поэтому rot rot E = - 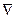 2E. Подставляя в правую часть (5.5) значение rot Н из (5.3), получаем
2E. Подставляя в правую часть (5.5) значение rot Н из (5.3), получаем
- 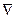 2E = jωμ·jωεE или
2E = jωμ·jωεE или 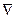 2E – ω2 μεE = 0. (5.5).
2E – ω2 μεE = 0. (5.5). 
Оператор 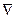 представляет собой сумму вторых производных по направлениям осей координат, например для декартовых координат это
представляет собой сумму вторых производных по направлениям осей координат, например для декартовых координат это
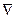 =
= 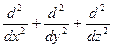 , для цилиндрических координат
, для цилиндрических координат 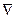 =
= 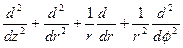 .
.
Таким образом, уравнение (5.5) приобретает вид:
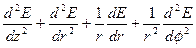 - k2E = 0 (5.6).
- k2E = 0 (5.6).
Это цилиндрическое (Бесселево) уравнение. Его решение
Ez = 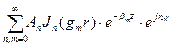 (5.7).
(5.7).
В выражении (5.7):
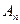 - постоянная, определяемая граничными условиями;
- постоянная, определяемая граничными условиями;
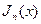 - функция Бесселя n -го порядка;
- функция Бесселя n -го порядка;
аргументами являются произведения gm r , β nz и nφ, где
gm - постоянная поперечного распространения;
βn - постоянная продольного распространения;
n и m – числа натурального ряда.
При этом
g12 = k12 – β2 - постоянная поперечного распространения для сердечника, (5.9);
g22 = β2 – k22 - постоянная поперечного распространения для оболочки, (5.10);
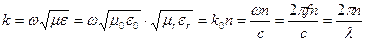 (5.11).
(5.11).
В выражении (5.11) :
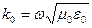 ; μ0 и ε0 - магнитная и диэлектрическая проницаемости вакуума; μr и εr - относительные магнитная и диэлектрические проницаемости сердцевины и оболочки;
; μ0 и ε0 - магнитная и диэлектрическая проницаемости вакуума; μr и εr - относительные магнитная и диэлектрические проницаемости сердцевины и оболочки;
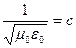 - скорость света;
- скорость света;
коэффициент преломления сердцевины 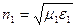 , оболочки
, оболочки 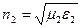 ;
;
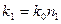 ;
; 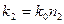 .
.
На рис.5.1 показаны Бесселевы функции нулевого и первого порядка (они похожи на затухающие косинусоиду и синусоиду). Аналогично выглядят и функции более высокого порядка. Пересечения этих кривых с осью аргументов x = gm r определяют значения корней, обращающих функции Jn в 0, и являющиеся решениями уравнения. Как видим решений бесконечно много, но они расположены не непрерывно, а дискретно, то есть не каждая волна или не каждый луч, даже если он в пределах апертурного угла, может распространяться по световоду.
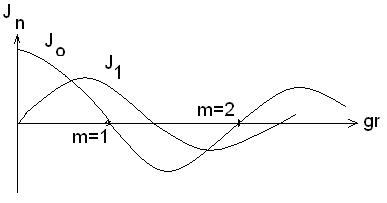
Рис.5.1. Вид Бесселевых функций
Каков смысл величин индексов n и m? Как мы уже отмечали раньше, в волокне распространяются только такие моды, у которых по диаметру волокна помещается целое число полуволн. Таким образом m - это число полуволн по окружности волокна, а n - число полуволн по диаметру. В таблице 5.1 приведены величины корней gr для некоторых значений m и n. Эти значения иногда называют нормированной частотой ν.
Таблица 5.1. Таблица значений нормированной частоты ν для некоторых m и n .
| n ↓ | Значения gr при m = | Тип волны | |||
| ….. | |||||
| 2.405 | 5.52 | 8.65 | …… | E0m | |
| 3.83 | 7.02 | ….. | Enm | ||
| 3.83 | 7.02 | 10.2 | …… | Hnm | |
| 2.45 | 5.54 | 8.67 | ….. | Enm | |
| 5.14 | 8.42 | 11.6 | ….. | Hnm | |
| ….. | ….. | ….. | …… | ….. | ….. |
При произвольном значении индексов в волокне возможно существование множества волн. Например, положим m = 3 , а n = 2. При распаде волны Н23 может возникнуть 13 мод!
Если возьмём значения m =1 и n = 0 -1, то из таблицы 5.1 видно, что при p = gr от 0 до 2.405 может существовать только одна мода Е01.
При распространении произвольной волны по сердцевине и оболочке волокна имеет место соотношение
g12 + g22 = k12 – β2 + β2 – k22 = k12– k22 = k02 (n12 – n22 ) (5.12).
Если имеет место полное внутреннee отражение, то g2 = 0, и свет распространяется только по сердцевине, и тогда
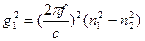 (5.13).
(5.13).
Из (5.13) получаем для частоты f1 (домножив числитель и знаменатель на величину радиуса сердцевины r = a) выражение:
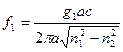 , или
, или 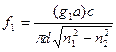 (5.14).
(5.14).
Таким образом для каждого решения pmn= ga существует своя мода, своя критическая частота, или, соответствующая ей длина волны
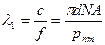 (5.15), где
(5.15), где 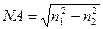 - апертура волокна.
- апертура волокна.
Если pnm = ν = 2.405, то из (5.15) получаем условие одномодовости:
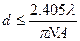 (5.16).
(5.16).
В типичном случае λ = 1.55 мкм, NA = 0.14 и диаметр одномодового волокна равен 6-10 мкм.
С увеличением диаметра число мод N в волокне резко возрастает:
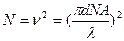 - для ступенчатого волокна, (5.17);
- для ступенчатого волокна, (5.17);
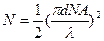 - для градиентного волокна, (5.18).
- для градиентного волокна, (5.18).
Волновое сопротивление оптического волокна заключено в пределах
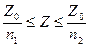 , где
, где 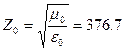 Ом – волновое сопротивление вакуума.
Ом – волновое сопротивление вакуума.
Ход волнового сопротивления волокна показан на рис. 5.2.
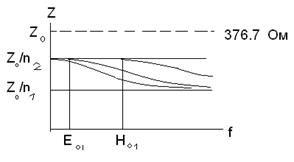
Рис. 5.2. Изменение волнового сопротивления для некоторых мод в зависимости от частоты

Дата добавления: 2015-01-13; просмотров: 1859;
