Нелинейные явления в оптическом волокне

Желание передать сигнал на возможно большее расстояние заставляет увеличивать мощность передаваемого сигнала. В то же время увеличение мощности сигналов приводит к целому ряду нелинейных откликов (явлений) в оптическом волокне. К ним относятся:

1.Нелинейность коэффициента преломления

2.Фазовые самомодуляция и кроссмодуляция (ФСМ и ФКМ).

3.Четырёхволновое смешение

4.Вынужденное неупругое рассеяние Мандельштама-Бриллюэна

5.Комбинационное рассеяние Рамана

Рассмотрим каждое из этих явлений по отдельности

6.1.Нелинейность коэффициента преломления.

Вектор индукции в общем виде равен

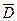= ε ₀∙ε_r∙ 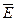(6.1).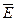

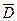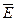В вакууме = ε₀∙ , в веществе 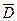= ε₀∙ _Σ ,

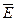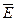где _Σ = 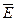+ 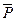, 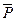– вектор поляризации молекул.

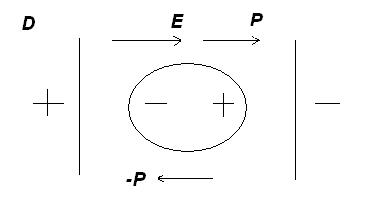
Рис. 6.1. Векторы электрического поля в пространстве около молекулы

При небольших полях Р линейно зависит от Е

P = kE

В этом случае

D = ε₀∙E_Σ = ε₀∙ (E+P) = ε₀ ∙ (E+kE) = ε₀ ∙ E(1+k) = ε₀ ε_r E (6.2),

где ε_r = 1+k, а

коэффициент преломления n = (ε_r)^½ =(1+k)^½ (6.3).

Если величина поля велика, то зависимость Р от Е не линейна (так же как в эспандере: зависимость растяжения эспандера от приложенной силы при большом растяжении становится не линейной) и её можно представить в окрестности интересующей точки в виде ряда Тэйлора

P = kE+ k₁E² + k₂E³ +…….- ряд Тэйлора и, соответственно,

n = ( 1+k+ k₁E + k₂E²+…)^½ (6.4).

В реальных условиях k₁≈ 0, и коэффициенты при более высоких степенях Е чем Е² также близки к 0, поэтому

n = (1+k + k₂E²+…)^½ ≈ n(ω) +Δn(E²). (6.5).

Таким образом, при сильных полях появляется дополнительная составляющая n, зависящая от Е². Коэффициент преломления сердцевины волокна изменяется, и вместе с ним изменяются и другие параметры волокна, в том числе скорость распространения.

6.2.Фазовая самомодуляция и кроссмодуляция (ФСМ и ФКМ)

Фаза сигнала по длине меняется как

φ = n∙k₀∙L где k₀= 2π/λ (6.6).

При большой мощности сигнала

n = n(ω)+Δn(E²)

В этом случае

φ= [n(ω)+Δn(E²)]∙k₀∙L= n∙k₀L+Δn(E²)∙k₀∙L (6.7),

где Δn(E²)∙k₀∙L = Δφ_нел – нелинейный набег фазы.

Пусть сигнал – гармонический и подчиняется, например, косинусоидальному закону. Из тригонометрии известно:

сos(φ+Δφ_нел) = cosφ∙cosΔφ – sinφ∙ sinΔφ

Δφ – величина небольшая, поэтому sinΔφ ≈ 0,

и тогда cos(φ+Δφ) ≈ cosφ∙cosΔφ,

откуда видно, что в результате набега фазы происходит дополнительная модуляция сигнала, которая называется фазовой самомодуляцией.

Если передаётся несколько длин волн (системы волнового уплотнения WDM), то воздействие сигнала большой мощности на одной из длин волн приводит к нелинейности во всём волокне – фазовой кроссмодуляции ФКМ. ФКМ обычно больше ФСМ.

φ_фкм = n(E₁²+2E₂²)∙k₀∙L (6.8).

Применительно к импульсам ФСМ имеет несколько особенностей: частота на переднем фронте уменьшается и увеличивается на заднем фронте.

6.3.Четырёхволновое смешение.

При большой величине поля волны начинают обмениваться энергией через посредство взаимодействия с электронными оболочками атомов, при этом среда в целом остаётся неизменной. Волокно играет пассивную роль среды, в которой волны разной длины взаимодействуют друг с другом через нелинейный отклик электронов внешних оболочек атомов. Это возможно, если дисперсия близка к нулю, и фазы волн не изменяются. В терминах квантовой механики четырёхволновое смешение - это уничтожение фотонов одной частоты и рождение фотонов другой частоты, причём суммарная энергия и импульс сохраняются.

Пусть на входе имеем две частоты ω₁ и ω_{2 .} После взаимодействия с электронными оболочками одна волна отдаёт часть своей энергии, а другая приобретает. На выходе кроме частот ω₁ и ω₂ появляются частоты ω₃ и ω₄. Из закона сохранения энергии следует

W₁ + W₂ = W₃ + W₄ или ћω₁ + ћω₂ = ћω₃ + ћω₄ (6.9),

где ћ- постоянная Планка, откуда

ω₁ + ω₂ = ω₃ + ω₄ (6.10).

При этом должен осуществляться фазовый синхронизм или согласованность фаз, т. е.

Δk = k₁+ k₂ − k₃ − k₄ ≈ 0 (6.11), где k_i= n_iω_i/c .

При нулевой дисперсии в волокне это условие выполняется, и использование систем волнового уплотнения WDM (когда в одном окне прозрачности передаётся сразу несколько волн) становится невозможным, так как сигналы комбинируют между собой. При наличии дисперсии согласованность фаз не сохраняется, поэтому при использовании систем волнового уплотнения WDM с оптическими усилителями дисперсия в диапазоне работы оптического усилителя должна быть отлична от нуля, чему соответствуют волокна рекомендации G.655.

Некоторые частные случаи 4-х волнового смешения:

1) Вырожденное или трёхволновое смешение

При мощной накачке генерируются две близких

волны

2ω₁= ω₂+ω₃ или ω₁−ω₃ = ω₄−ω₁ (6.12),

где ω₃ и ω₄ − стоксова и антистоксова компоненты.

2)Параметрическое усиление

Если имеется сильная накачка на частоте ω₁ и одновременно вводится слабый сигнал ω₃ , то возникает сильный сигнал ω₃ и слабый ω₄ :

ω₁ + ω₃ = ω₃ + ω₄ (6.13).

3)Параметрические процессы третьего порядка.

Иногда наблюдается генерация спектральных компонент – вторых и суммарных гармоник типа

2ω₁ , 2ω₂ , 2ω₁ + ω₂ , 2ω₂ + ω₁

Генерация гармоник высшего порядка составляет малую величину от основного процесса. Уровень понимания этих процессов ещё далёк от совершенства.

4)Поляризационная неустойчивость, когда ортогональные оси в волокне при увеличении мощности меняются местами.

6.4.Вынужденное неупругое рассеяние Мандельштамма-Бриллюэна

При небольшой мощности передаваемых сигналов поток фотонов при столкновениях с молекулами кварца в волокне испытывает упругие столкновения как теннисные или бильярдные шары при ударе о стенку. Это явление называется релеевским рассеянием. Молекулы кварца испытывают температурные колебания и, следовательно, смещения из положения равновесия. Если поток фотонов очень большой, то часть электронов колеблющихся атомов сбивается фотонами, происходит поглощение фотона и переход электрона в возбуждённое состояние. Электрон спонтанно возвращается обратно, но необязательно на ту же орбиту, с которой был сбит, при этом испускается квант света меньшей энергии. Это похоже на столкновение пластилинового шарика со стенкой. Шарик отскакивает, но при этом деформируется – происходит неупругое столкновение.

W_пад= W_отр + ΔW (6.14),

где W_пад- энергия падающего фотона,

W_отр- энергия излученного (отражённого) фотона,

ΔW – дефицит энергии.

Переходя к квантовой форме записи, получаем

ћω_пад = ћω_отр + ћΔω или ω_пад = ω_отр+ Δω (6.15),

где ω_отр- отражённая (излученная) частота, которая как правило меньше падающей и распространяется в обратном направлении (как мячи от стенки) и называется Стоксовой волной.

Δω- низкочастотная составляющая, которая проявляется в виде механических колебаний материала волокна со звуковой частотой. Это колебание в виде сгустка сжатий и разряжений, называемого фононом, распространяется по волокну с относительно малой скоростью (≈ 5 км/сек), вызывая временное локальное изменение свойств волокна.

Это явление получило название вынужденного неупругого рассеяния Мандельштама-Бриллюэна. Оно возникает в диапазоне мощности от 10 до 100 мВт (в зависимости от диаметра волокна).

Это явление может быть объяснено и без привлечения квантовой механики на основе пьезоэффекта и электрострикции. Известно, что когда к кристаллу кварца прикладывается переменное напряжение, в кристалле возникают механические колебания.

Ширина полосы излучения ВРМБ порядка 10 МГц.

6.5.Комбинационное рассеяние Рамана

При ещё большем увеличении мощности, передаваемой по волокну, в процесс комбинирования энергии кроме квантов падающего света вовлекается колебательная и вращательная энергия молекул. Этот эффект был открыт Мандельштамом и Ландсбергом в кварце (ещё в двадцатых годах ХХ – го столетия и Раманом в жидкости (в середине века). Часть фотонов меняет частоту по закону:

ω₀ = ω₁ ± Δω (6.16).

Изменение частоты соответствует либо уменьшению энергии фотона, отдавшего часть энергии на возбуждение рассеивающей системы (колебанию молекулы или переходу молекулы в другое колебательное состояние), либо увеличению энергии фотона за счёт энергии системы, колебания которой как-либо были возбуждены ранее (например, нагревом). Особенностями ВКР являются:

1) Порог возникновения явления 600 мВт - 1 Вт

2) Излучение системы в основном идёт в прямом направлении (сонаправленно с накачкой). Порог встречного излучения значительно выше.

3) При большой накачке интенсивность Стоксовой волны возрастает столь быстро (почти

экспоненциально), что вся энергия накачки переходит в Стоксову волну

4) В аморфных веществах, каким является плавленый кварц, полосы частот молекулярных колебаний перекрываются и создают континуум, в результате чего ВКР в кварце существует в широком диапазоне частот – до 40 ТГц с максимумом вблизи 13 ТГц.

Эти особенности ВКР создают условия для его использования в системах оптического усиления.

Нелинейные явления наряду с отрицательными последствиями, которые они вносят в процессы распространения сигналов, могут быть использованы для создания усилителей оптических сигналов и других пассивных компонент.