Вопрос 31: Уравнение Шредингера.

Э. Шредингер (1926) постулировал фундаментальное соотношение – основное уравнение нерелятивистской квантовой механики, справедливость которого (как и всяких постулатов) подтверждается согласием с опытом получаемых с его помощью результатов. Уравнение Шредингера – нерелятивистское уравнение относительно основной характеристики состояния микрообъектов – волновой функции ψ(r,t) – и имеет вид

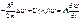, (79)

где ħ = h/(2π), m – масса частицы, Δ – оператор Лапласа 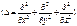, i – мнимая единица, U (r,t) – потенциальная функция частицы в силовом поле, в котором частица движется. Это уравнение называют временным уравнением Шредингера. Если силовое поле, в котором частица движется, стационарно, т. е. функция U (r) не зависит от времени и имеет смысл потенциальной энергии, то решение уравнения (79) можно искать в виде произведения двух функций, одна из которых есть функция только координат, другая – только времени: ψ(r,t) = ψ(r)·φ(t) (80)

Подставив функцию (80) в уравнение Шредингера (79) и разделив левую и правую части на произведение ψ(r)·φ(t), получим

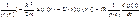(81)

Так как левая часть уравнения (81) зависит только от r, а правая – только от t, то их можно приравнять одной и той же постоянной разделения, в качестве которой, как можно показать, можно выбрать Е – полную энергию частицы. Таким образом,

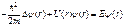(82)

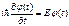(83)

Уравнение (82) называют стационарным уравнением Шредингера. Его обычно записывают в более удобном виде:

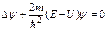(84)

Явный вид стационарного уравнения Шредингера определяется конкретной зависимостью U (r).

Решая уравнение (83), получаем, что 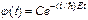, (85)

где С – произвольная постоянная. Подставляя (85) в (80), видим, что в случае стационарного силового поля состояние частицы описывается волновой функцией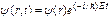

[постоянная С включена в функцию ψ(r)], откуда следует, что стационарность состояния не исключает зависимости волновой функции от времени, а только ограничивает ее гармоническим законом 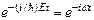. В стационарном состоянии плотность вероятности 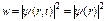выражается только через ψ(r) и не зависит от времени. Общепринято ψ(r) также называть волновой функцией, хотя она является только координатной (амплитудной) частью волновой функции ψ(r,t) стационарного состояния. Временное уравнение Шредингера имеет вид [см. (79)]

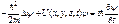, (102)

где ψ = ψ(x,y,z,t). С учетом того, что гамильтониан 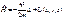, уравнение (102) примет вид 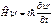(103)

– уравнение Шредингера в операторной формеПодставив в стационарное уравнение Шредингера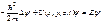

оператор полной энергии [см. (101)] ,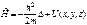

получим стационарное уравнение Шредингера в операторной форме: 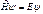(104)