Вопрос 30: Волновая функция.

Однако в общем случае состояние частицы в квантовой механике задается более сложной, вообще говоря комплексной, функцией ψ(r,t), зависящей от координат и времени. Эту функцию называют волновой функцией. В частном случае свободного движения частицы волновая функция переходит в плоскую волну де Бройля.

Вероятность dW нахождения частицы в элементе объема dV в момент времени t, согласно статистической интерпретации ψ - функции,

.

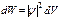Величина 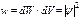имеет смысл плотности вероятности, т. е. определяет вероятность нахождения частицы в момент времени t в окрестности данной точки пространства. Плотность вероятности – величина, наблюдаемая на опыте, в то время как сама волновая функция, являясь комплексной, наблюдению недоступна. В этом заключается существенное отличие в описании состояний частиц в квантовой и классической механике (в классической механике величины, описывающие состояние частиц, наблюдаемы). Вероятность найти частицу в момент времени t в некотором объеме V, согласно теореме сложения вероятностей

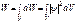(76)

Проинтегрировав выражение (76) в бесконечных пределах, получим вероятность того, что частица в момент времени t находится где-то в пространстве. Это есть вероятность достоверного события, а ее в теории вероятностей считают равной 1. Поэтому принимают, что

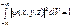(77)

Условие (77) называют условием нормировки, а функцию ψ – нормированной волновой функцией. Так как волновая функция – объективная характеристика состояния микрочастиц, то она должна удовлетворять ряду ограничений. Она должна быть конечной (вероятность не может быть больше единицы), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком). В квантовой механике для волновых функций выполняется принцип суперпозиции состояний: если какая-либо система (частица или их совокупность) может находиться в различных состояниях, описываемых волновыми функциями ψ₁, ψ ₂, …, ψ _n, то она может находиться в состоянии ψ, описываемом линейной комбинацией этих функций: ,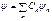

где С_n (n = 1, 2, ...) – произвольные (в общем случае комплексные) числа, при этом квадрат модуля коэффициента С_n т. е. \ С_n\², равен вероятности обнаружить, что система, представленная состоянием ψ, может оказаться в состоянии ψ_n.