Вопрос 28: Волны Де Бройля.

Луи де Бройль в 1924 г. постулировал, что корпускулярно-волновой дуализм имеет универсальный характер и распространяется не только на световые корпускулы (фотоны), но и на все частицы материи: частицы вещества (в частности, электроны) наряду с корпускулярными обладают также и волновыми свойствами. Количественные соотношения, связывающие корпускулярные (энергия и импульс) и волновые [частота (длина волны)] характеристики микрочастиц, такие же, как для фотона:

E = hv = ħω, p = h/λ = ħk, где k = 2π/λ – волновое число, а ħ = h/2π – постоянная Планка.

Длина волны, связанная с частицей, 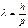, (71)

где р – импульс частицы, λ называется длиной волны де Бройля.

Для нерелятивистской частицы длина волны де Бройля 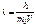, где т₀ – масса покоя частицы. Если Т – кинетическая энергия частицы [Т=р²/(2т)], то 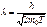(71)

Для релятивистской частицы длина волны де Бройля

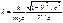
(в данном случае 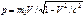). Выразив с помощью соотношения 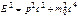импульс частицы р через ее полную энергию Е, найдем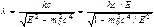

Если Т – кинетическая энергия частицы, то Е = Т + т₀с².

Тогда .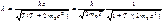

Гипотеза де-Бройля была блестяще подтверждена экспериментально. Дэвиссон и Джермер обнаружили, что пучок электронов, рассеивающийся от кристаллической пластинки, дает дифракционную картину. Томсон и независимо от него Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу. Экспериментальное доказательство наличия волновых свойств микрочастиц привело к выводу о том, что мы имеем дело с универсальным явлением – общим свойством материи Простейшей волной с частотой ω и волновым вектором k является плоская монохроматическая волна

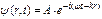, (72)

где А – постоянная амплитуда волны, k – волновой вектор (его направление совпадает с направлением распространения волны, а модуль равен 2π/λ).

Согласно корпускулярно-волновому дуализму материи, ω = E/ħ и р = ħk. Учитывая эти соотношения и выражение (72), видим, что с движением частицы, имеющей определенные энергию и импульс, связывается волна вида ,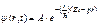

называемая плоской волной де Бройля.