Вопрос 34: Квантовый осциллятор
Линейный (одномерный) гармонический осциллятор – система, совершающая одномерное движение под действием квазиупругой силы. Потенциальная энергия линейного гармонического осциллятора
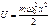 , (113)
, (113)
где т – масса частицы, ω0 – собственная частота колебаний осциллятора, х – отклонение от положения равновесия. Зависимость (113) имеет вид параболы (рис. 65), т. е. «потенциальная яма» в данном случае является параболической. Оператор Гамильтона для осциллятора в квантовой теории имеет вид 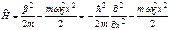 . (114)
. (114)
Рис. 65
Записав стационарное уравнение Шредингера в операторной форме [см. (104)] 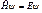 и учитывая (114), придем к уравнению Шредингера для гармонического осциллятора
и учитывая (114), придем к уравнению Шредингера для гармонического осциллятора
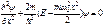 , (115)
, (115)
где Е – полная энергия осциллятора.
Опуская подробное решение волнового уравнения (115) приведем полученные собственные функции линейного гармонического осциллятора 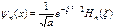 , (116)
, (116)
где 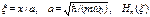 – полином Чебышева-Эрмита n - го порядка:
– полином Чебышева-Эрмита n - го порядка: 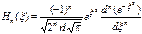 ;
;
функции (116) нормированы так, что 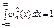 .
.
Нормированные волновые функции стационарных состояний квантового осциллятора: 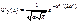 (n = 0) (117)
(n = 0) (117)
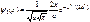 (n = 1) (118)
(n = 1) (118)
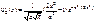 (n = 2) (119)
(n = 2) (119)
Анализируя волновые функции (117) – (119), видим, что функция (117) вообще не обращается в нуль (кроме 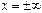 ), функция (118) обращается в нуль при х = 0. Точка, в которой волновая функция обращается в нуль, называется узлом. Функция (119) обращается в нуль при
), функция (118) обращается в нуль при х = 0. Точка, в которой волновая функция обращается в нуль, называется узлом. Функция (119) обращается в нуль при 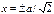 , т. е. имеет два узла. Таким образом, квантовое число определяет число узлов собственной волновой функции.
, т. е. имеет два узла. Таким образом, квантовое число определяет число узлов собственной волновой функции.
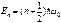 (п = 0, 1, 2, ...). (120)
(п = 0, 1, 2, ...). (120)
Формула (120) показывает, что энергия квантового осциллятора может иметь лишь дискретные значения, т. е. квантуется.
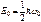 . При
. При 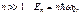 т. е. энергетические уровни осциллятора совпадают с величинами квантованной энергии осциллятора, постулируемыми Планком в теории излучения черного тела.
т. е. энергетические уровни осциллятора совпадают с величинами квантованной энергии осциллятора, постулируемыми Планком в теории излучения черного тела.
Из формулы (120) вытекает важный результат: минимальная энергия квантового осциллятора 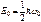 , т. е. его энергия не может обращаться в нуль (конечно, при ω0 ≠ 0), в то время как в классической теории энергия основного состояния – состояния покоя – равна нулю. Существование минимальной энергии (энергия нулевых колебаний) является типичной для квантовых систем и представляет собой прямое следствие соотношения неопределенностей.
, т. е. его энергия не может обращаться в нуль (конечно, при ω0 ≠ 0), в то время как в классической теории энергия основного состояния – состояния покоя – равна нулю. Существование минимальной энергии (энергия нулевых колебаний) является типичной для квантовых систем и представляет собой прямое следствие соотношения неопределенностей.
Плотность вероятности обнаружить частицу на оси х определяется квадратом модуля волновой функции 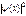 .
.
Дата добавления: 2015-02-25; просмотров: 1290;
