Вопрос 36: Квантовая модель атома водорода.

Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z = 1), 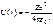, (142)

где r – расстояние между электроном и ядром. Состояние электрона в атоме водорода описывается волновой функцией ψ, удовлетворяющей стационарному уравнению Шредингера [см. (84)], учитывающему значение (142):

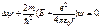(143)

где т – масса электрона, Е – полная энергия электрона в атоме. Кулоновское поле ядра, в котором движется электрон, является центрально-симметричным, поэтому уравнение (142) целесообразно решать в сферических координатах 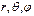, считая, что .

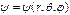Оператор Лапласа в сферических координатах задается известной формулой ,

где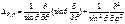

– угловая часть лапласиана. Тогда уравнение Шредингера для стационарных состояний (144)

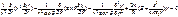
Анализ угловой части уравнения приводит к выводу, что его однозначные, конечные и непрерывные решения во всей области изменения переменных θ и φ имеют место при значениях параметра 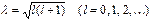, а также при условии .

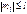2. Энергия– получаемым из уравнения Шредингера собственным значениям энергии (146)

в точности совпадающим с уровнями энергии в модели атома Бора!

Энергия ионизации атома водорода равна

.

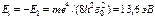3. Квантовые числа. Общее решение уравнения Шредингера (144) записывается в виде ,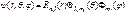

где 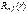– радиальная волновая функция, зависящая только от r (n и l – целые числа), функция 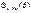имеет два целочисленных индекса: l и m_l, функция 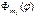– один целочисленный индекс m_l.

Целое число п, называемое главным квантовым числом, совпадает с номером уровня энергии [см. (146)], определяя энергию электрона в атоме;оно может принимать только целые положительные значения: n = 1, 2, 3, ... .

Целые числа l и m_l, представляют собой орбитальное и магнитное квантовые числа.

Согласно формулам (95) и (98)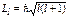

(определяет модуль момента импульса электрона) и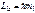

(определяет проекцию момента импульса электрона на направление z внешнего магнитного поля).

Так как при данном п орбитальное квантовое число l может принимать значения от 0 до n - 1, а каждому значению l соответствуют 2l+1 различных значений m_l то кратность вырождения уровней водорода 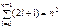. (147)

4. Энергетический спектр. Квантовые числа п, l, и т_l позволяют более полно описать спектр испускания (поглощения) атома водорода, чем это делает теория Бора.

1) изменение орбитального квантового числа Δl удовлетворяет условию 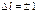, (148)

2) изменение магнитного квантового числа Δm_l, удовлетворяет условию .