Устойчивость равновесия линейной системы с N степенями свободы

В общем случае система описывается 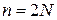линейными уравнениями I-го порядка

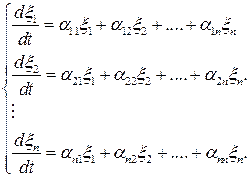. (6.23)

Предположим, что 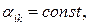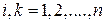, и детерминант, составленный из этих коэффициентов, отличен от нуля

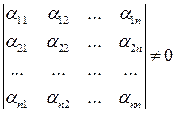. (6.24)

Уравнение (6.23) является обобщением уравнения (6.9).

В состоянии равновесия все производные равны нулю, так как во времени не изменяется ни одна из координат

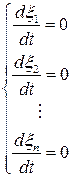. (6.25)

Система уравнений, из которых определяются координаты состояния равновесия, примет вид:

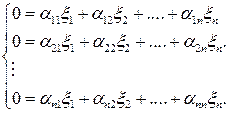. (6.26)

Поскольку 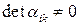, все координаты равны нулю:

.

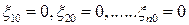Состояние равновесия расположено в начале координат.

Исследуем поведение системы вблизи состояния равновесия.

Найдем точное решение (6.12), пользуясь методом Эйлера. Для любой координаты частное решение есть

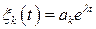, (6.27)

где .

Подставим (6.27) в (6.23)

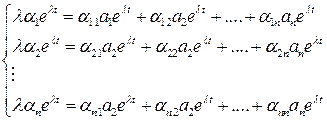, (6.28)

сократим на 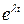и соберем коэффициенты при одинаковых :

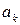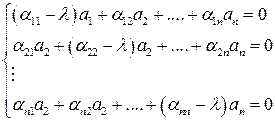. (6.29)

Получили систему однородных уравнений относительно 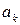, к = 1, … , n. Чтобы хотя бы одно из них было отлично от нуля, нужно чтобы детерминант (6.14) был равен нулю:

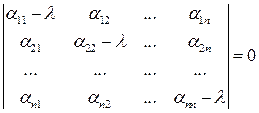. (6.30)

Если раскрыть этот детерминант, собрать коэффициенты при одинаковых степенях 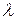, то получим алгебраическое уравнение относительно (характеристическое уравнение);

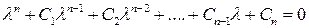, (6.31)

где 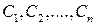– постоянные, зависящие от .

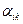Характеристическое уравнение (6.31) в общем случае имеет 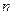корней, так как уравнение n-ого порядка; .

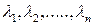Общее решение для любой координаты есть суперпозиция частных:

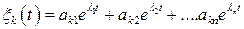. (6.32)

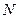постоянных 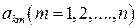а_km (m = 1, 2, … , n) независимы и определяются начальными условиями. Остальные постоянные 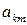связаны между собой уравнениями (6.29).

Из общего решения (6.32) видно, что поведение координат со временем определяется экспонентами .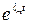

В общем случае корни комплексные

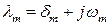, где 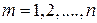. (6.33)

Если хотя бы одно значение δ_m > 0, соответствующая экспонента стремится к бесконечности, следовательно ξ_k (t) → ∞ при t → ∞; система уходит от положения равновесия. Состояние равновесия неустойчиво. Если все вещественные части корней отрицательны (δ_m < 0, m = 1, … , n), то в этом случае ξ_k (t! → 0) при t → ∞, т.е. система стремится перейти в положение равновесия. Состояние равновесия абсолютно устойчиво.

Если вещественные части хотя бы у одной пары комплексно-сопряженных корней равны нулю, а остальные δ_m < 0, то частным решением системы (6.12) будет гармоническое колебание. Система будет совершать движение около положения равновесия, не достигая его. Состояние равновесия устойчиво по Ляпунову.

В результате анализа можно сделать вывод: для того, чтобы оценить устойчивость равновесия линейной системы, не обязательно знать корни характеристического уравнения (6.16); достаточно иметь сведения о знаках вещественных частей корней.

Для этой цели служит критерий Рауса-Гурвица. Он устанавливает необходимые и достаточные условия того, чтобы реальные части всех корней характеристического уравнения были отрицательными. В этом случае состояние равновесия системы абсолютно устойчиво.

Пусть характеристическое уравнение имеет вид:

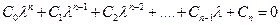. (6.34)

(В нашем случае (6.31) ).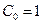

1. Необходимым условием того, чтобы вещественные части корней характеристического уравнения были отрицательны, является требование: все коэффициенты 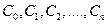характеристического уравнения должны быть положительны. Если хотя бы один из этих коэффициентов отрицателен, то обязательно найдется хотя бы один корень с положительной реальной частью и состояние равновесия будет неустойчивым.

2. Для формулирования достаточного условия необходимо их коэффициентов уравнения (6.19) составить матрицу Гурвица. Правило составления матрица следующее;

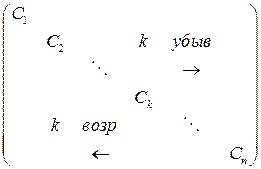. (6.35)

Матрица квадратная. Диагональными элементами являются коэффициенты уравнения (6.34), начиная с 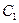. В строках матрицы записываются коэффициенты: с убывающими номерами вправо от диагонали, с возрастающими – влево. Если соответствующие коэффициенты отсутствуют, записывают нули.

Матрица Гурвица для (6.34) имеет вид:

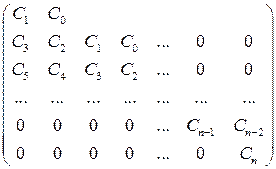. (6.36)

Достаточным условием того, чтобы вещественные части корней характеристического уравнения были отрицательными, является выполнение следующих неравенств:

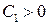, (6.37)

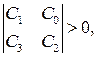(6.38)

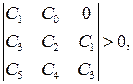6.39)

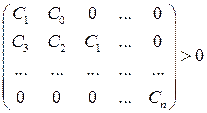. (6.40)

т.е. диагональные миноры определителя Гурвица должны быть положительными.

Исследование устойчивости состояния равновесия нелинейной системы по первому приближению (второй метод Ляпунова)

В общем случае нелинейная система с N степенями свободы описывается 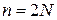нелинейными уравнениями 1-го порядка

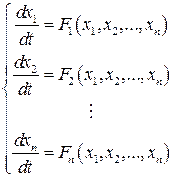, (6.41)

где 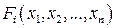– нелинейные функции своих аргументов.

Системы динамических уравнений (6.41) будем считать стандартной и дальнейшие рассуждения будут проводиться применительно к этой форме. Если динамические уравнения имеют другую форму, то путем замен и преобразований их можно привести к стандартной форме.

Состояние равновесия такой системы определится из обычного условия стационарности, когда производные равны нулю:

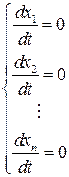. (6.42)

Получаем систему нелинейных алгебраических уравнений

. (6.43)

Из системы уравнений (6.43) находим координаты, в которых система находится в состоянии равновесия;

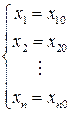. (6.44)

В общем случае число корней уравнения (6.43) может быть больше n, т.е. у системы существует несколько состояний равновесия. Какое их них реализуется – и является целью исследования устойчивости. Второй метод Ляпунова указывает, как проводить это исследование и, главное, формулирует условия (теоремы Ляпунова), которые гарантируют правильность полученных результатов.

Для исследования устойчивости состояния равновесия с координатами 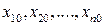, нелинейной системе (6.41) сопоставляется некоторая возмущенная система. Для этого предполагается, что координаты х_i мало отличаются от равновесных

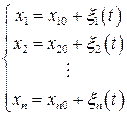, (6.45)

где все .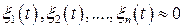

Ввиду малости 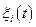ξ_i нелинейные функции в (6.41) можно разложить в ряд около состояния равновесия;

.

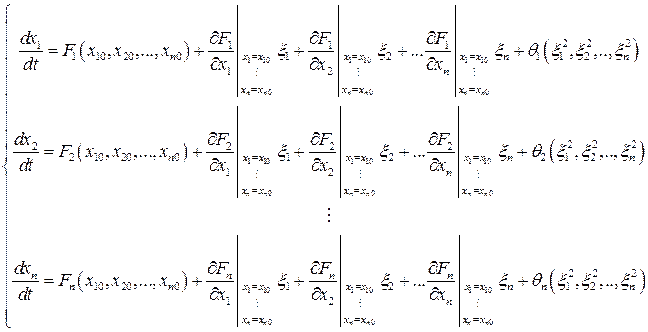(6.46)

где 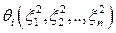- нелинейные члены, порядок малости которых не меньше 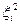. Постоянные составляющие равны нулю в состоянии равновесия (6.23).

Отбрасывая нелинейные члены 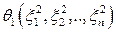, , 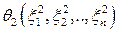…, , 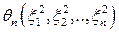получим систему первого приближения;

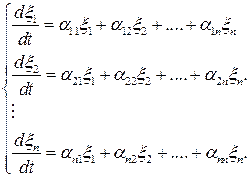. (6.47)

Легко увидеть, что система первого приближения (6.47) ничем не отличается от линейной системы (6.23), устойчивость которой исследована выше.

Ляпунову принадлежат три фундаментальных теоремы об устойчивости равновесия нелинейной системы. Сформулируем их без доказательств.

1. Теорема об устойчивости по первому приближению

Если все корни характеристического уравнения системы первого приближения (6.47) имеют отрицательные вещественные части, то соответствующее состояние равновесия нелинейной системы (6.41) асимптотически устойчиво.

Другими словами, из асимптотической системы первого приближения следует асимптотическая устойчивость исходной системы.

2. Теорема о неустойчивости по первому приближению

Если среди корней характеристического уравнения системы первого приближения (6.47) встречается хотя бы один корень с положительной вещественной частью, то состояние равновесия нелинейной системы неустойчиво.

3. Теорема об особенных случаях

Если среди корней характеристического уравнения системы первого приближения (6.47) встречается хотя бы один корень с нулевой вещественной частью, то невозможно сделать заключение об устойчивости или неустойчивости равновесия нелинейной системы.

Чтобы решить вопрос об устойчивости в особенных случаях, необходимо учитывать, по крайней мере, второе приближение в уравнениях (6.46). Однако уравнения возмущенной системы становятся нелинейными и трудности анализа резко возрастают.

Значение теорем Ляпунова для практики огромно. Еще до проведения эксперимента можно найти и проанализировать устойчивые стационарные состояния нелинейной системы, которые будут осуществляться в действительности.

Проиллюстрируем второй метод Ляпунова на примере исследования устойчивости маятника с затуханием. Динамическое уравнение системы при любых углах отклонения имеет вид:

, (6.48)

где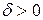

Приведем уравнение (6.48) к стандартной форме. Пусть

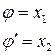. (6.49)

Тогда

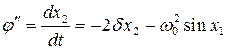. (6.50)

Уравнение (6.48) преобразуется к виду

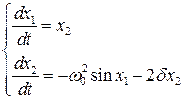. (6.51)

Из (6.51) найдем состояние равновесия

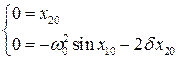. (6.52)

Отсюда 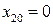, а из 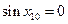получим, что 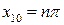, где n = 0, ±1, ±2, … . Физический смысл имеют два положения равновесия:

1. 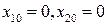, - маятник в нижнем положении,

2. 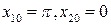- маятник в верхнем положении.

1. Исследуем нижнее состояние равновесия: .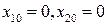

Тогда из (6.45) получим:

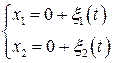. (6.53)

Подставляем в (6.51) и раскладываем в ряд (см.(6.46));

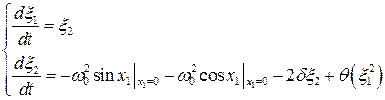. (6.54)

Отбросим нелинейные члены и получим систему первого приближения;

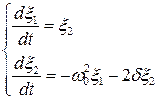. (6.55)

Матрица коэффициентов уравнения первого приближения:

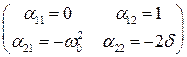. (6.56)

Характеристическое уравнение получим, раскрыв детерминант (6.30):

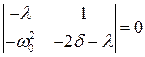. (6.57)

Применим критерий Рауса-Гурвица. Матрица Гурвица:

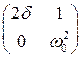. (6.58)

Определители Гурвица:

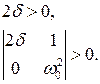. (6.59)

Поскольку 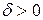и необходимое и достаточное условие выполняются. Следовательно, 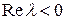для любого корня. На основании первой теоремы Ляпунова делаем вывод об асимптотической устойчивости нижнего положения равновесия маятника.

II. Исследуем устойчивость верхнего состояния равновесия:

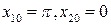. (6.60)

Дадим возмущение

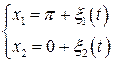. (6.61)

Разложим правые части уравнений (6.51) в ряд:

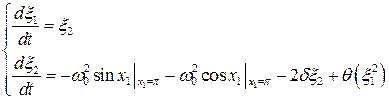, (6.62)

и найдем систему первого приближения:

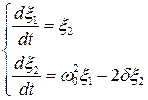. (6.63)

Характеристическое уравнение будет иметь вид:

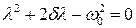. (6.64)

Необходимое условие критерия Рауса-Гурвица нарушено, так как последний коэффициент характеристического уравнения отрицательный, следовательно, 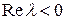, хотя бы для одного корня. На основании второй теоремы Ляпунова об устойчивости делаем вывод, что верхнее положение равновесия маятника неустойчиво.

В качестве второго примера использования методологии Ляпунова рассмотрим вопрос о своеобразной неустойчивости равновесия в области застоя для системы с кулоновским трением (Рис.44).

Исследование проведем на фазовой плоскости. Если отклонение , то движение отсутствует, система находится в состоянии равновесия. Следует идее Ляпунова, дадим возмущение. Для простоты и наглядности рассуждений будет считать, что возмущению подвергается лишь скорость, причем величина возмущения будет одинакова во всех случаях, а знак скорости меняется от опыта к опыту.

Рассмотрим движение изображающей точки, если есть одно положительное и одно отрицательное возмущение скорости. Пусть из состояния равновесия 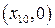система переводится в состояние 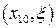), откуда со временем переходит в новое состояние равновесия .

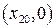Состояние равновесия 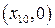обладает своеобразной «неустойчивостью» - система, выведенная из него, обратно в него же не возвращается.

То же самое можно сказать и о состоянии 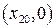. Если система получит возмущение по скорости (в этом опыте отрицательное), то она переходит в новое состояние равновесия 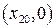. Интересно отметить следующее; после двух разных по знаку возмущений по скорости изображающая точка приблизилась к середине области застоя – началу координат. Приближение к началу координат можно исследовать аналитически, доказав неравенство

. (6.65)

В верхней полуплоскости изображающая точка движется по эллипсу (5.40)

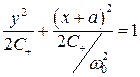, (6.66)

где С₊ определяется из условия: при 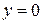и

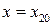
. (6.67)

При , 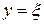и из (5.40)

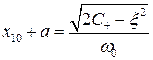. (6.68)

Взяв разность (6.67) и (6.68), преобразуя, получим

. (6.69)

В нижней полуплоскости изображающая точка движется по эллипсу (5.40)

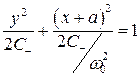. (6.70)

При 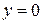, , 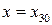тогда

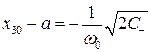. (6.71)

При 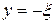, , 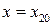тогда

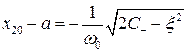. (6.72)

Взяв разность (6.71) и (6.72), получим

. (6.73)

Сравнивая (6.67) и (6.71) и учитывая, что , получаем . Отсюда знаменатель (6.69) больше знаменателя (6.68) и, как следствие, справедливость (6.65).

Придавая возмущение по скорости многократно, при условии равновероятности отклонения, можно приблизиться к положению равновесия (0,0) как угодно близко. Середина области застоя соответствует асимптотически устойчивому состоянию равновесия.

Этот факт используется на практике. Известно, что стрелочные электроизмерительные приборы не выставляются на точный нуль после измерения, что обусловлено кулоновскими трениями в подшипниках. Слегка постукивая по прибору, т.е. давая возмущение по скорости, удается перевести стрелку в абсолютное состояние равновесия и этим повысить точность отсчета.

Глава VII. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В СИСТЕМАХ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ (ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ)

Вынужденные колебания наблюдаются в системах при внешнем силовом воздействии. Это воздействие должно иметь ту же физическую природу, что и система, на которую оно действует. Обычно предполагается, что внешний источник действует бесконечно долго, так что собственные колебания к моменту наблюдения затухли и в системе сохраняются только вынужденные колебания.

Если воздействие прекращается, вынужденные колебания исчезают. Получим динамическое уравнение системы при силовом воздействии. В качестве примера рассмотрим последовательный колебательный контур под действием источника ЭДС (Рис.45).

Применяя второй закон Кирхгофа, получим уравнение для заряда:

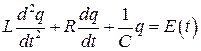. (7.1)

Пусть в качестве искомой переменной будет напряжение на емкости

. (7.2)

Тогда, вводя стандартные обозначения

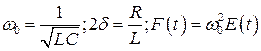, (7.3)

получим уравнение в стандартной форме

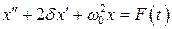. (7.4)

Если система нелинейная, уравнение в общем случае имеет вид:

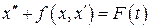. (7.5)

С математической точки зрения анализ вынужденных колебаний означает отыскание решения неоднородного дифференциального уравнения.

Решение нелинейного уравнения (7.5) в общем виде неизвестно, поэтому обычно рассматривают частные случаи. (В следующих лекциях рассмотрим задачу Дуффинга).

Для анализа линейных систем (7.1) существует ряд мощных методов: метод вариаций постоянной Лагранжа, метод Лапласа, метод Фурье и другие. Применение того или иного метода определяется в основном видом функции

Из теории обыкновенных дифференциальных уравнений известно, что общее решение неоднородного линейного уравнения (7.1) можно представить в виде:

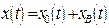, (7.6)

где 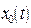- решение однородного уравнения (2.7); 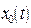представляет собственные колебания системы, которые подробно изучались выше. 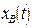- частные решения неоднородного уравнения, которое описывает вынужденные колебания. Найти и проанализировать его – наша задача. Важно помнить, что четкое разделение собственных и вынужденных колебаний возможно только в линейных системах. По существу – это следствие выполнения принципа суперпозиции в линейных системах.

Напомним содержание этого принципа применительно к уравнению (7.1).

Если - частное решение при 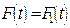, а 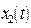- частное решение при 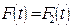, то при

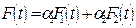, (7.7)

где 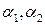- постоянные коэффициенты, частным решением уравнения будет

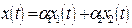. (7.8)

Легко проверить, что выражение (7.6) является частным случаем (7.8), соответствующим .

Для нелинейного уравнения (7.5) принцип суперпозиции не выполняется, поэтому выделение вынужденных колебаний в чистом виде невозможно.

Из всего многообразия внешних воздействий, особое значение имеет гармоническое воздействие. Из теории рядов Фурье и интеграла Фурье известно, что при определенных ограничениях (которые всегда выполняются на практике) функция времени может быть представлена в виде суммы гармонических колебаний. Кроме того, гармонические колебания относительно просто генерировать. Таким образом, гармоническая функция играет роль фундаментальной функции.

Поэтому исследование вынужденных колебаний в любой системе начинается обычно со случая гармонического воздействия.