Гармонический осциллятор при произвольном внешнем воздействии

Гармонический осциллятор при произвольном внешнем воздействий описывается неоднородном уравнением;

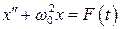, (8.54)

Найдём частное решение, пользуясь методом вариации постоянной Лагранжа. Ход рассуждений следующий. Если гармонический осциллятор без внешнего воздействия 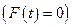, то его колебания чисто гармонические и амплитуды постоянны

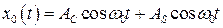. (8.55)

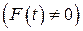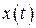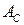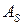Если на осциллятор действуют внешняя сила , то ищем ) в той же форме, но амплитуды и полагаем функциями времени (варьируем постоянные) и подбираем их так, чтобы

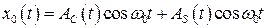. (8.56)

удовлетворяло уравнению (8.56) тождественно. Вместо одной неизвестной 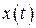имеем две: 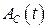и 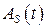. Чтобы связь 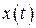и пары 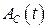, 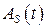была однозначной, необходимо, чтобы 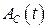, 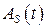были зависимыми. Как же выразить эту зависимость?

Найдём первую производную:

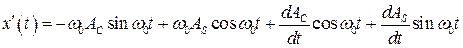. (8.57)

Лагранж предложил приравнять два последних слагаемых к нулю

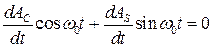. (8.58)

и тем самым получил уравнение связи между 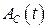и 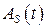. Замечательно, что производная (8.55) при условии (8.56) имеет тот же вид, что и для свободных колебаний. Вторая производная;

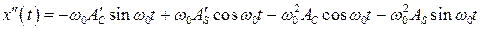. (8.59)

подставляя (8.56) и (8.59) в исходное уравнение (8.54), получим;

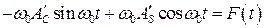. (8.60)

Выражения (8.58) и (8.60) образуют систему из двух уравнение с двумя неизвестными ;

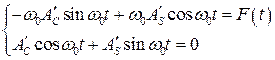. (8.61)

Рассматривая 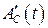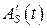_, как неизвестные, найдём их из (8.61);

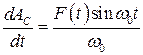, (8.62)

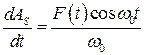. (8.63)

Уравнения (8.62) и (8.63) с разделяющими переменными, которые легко интегрируются

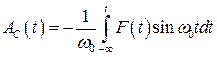, (8.64)

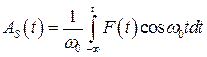. (8.65)

Как показывают полученные соотношения, вынужденное в линейной системе при произвольном внешнем воздействии ищется в виде квазигармонического колебания с частотой .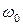

Литература

1. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М., ГИФМЛ, 1959.

2. Бабаков И.М. Теория колебаний. М., ГИТТЛ, 1958.

3. Бойко Б.П. Теория колебаний: конспект лекций для студентов IV курса вечернего отделения. Казань. Изд-во Казанског у-та, 1979.

4. Горелик Г.С. Колебания и волны. Введение в акустику, радиофизику и оптику: учеб. пособие для студ. вузов/ Г.С. Горелик. М.; Физматлит, 2007

5. Горяченко В.Д. Элементы теории колебаний: Учеб. пособие для вузов/ В.Д. Горяченко. М.; Высш. школа, 2001

6. Ильин М.М. Теория колебаний: Учебник для вузов/ М. М. Ильин, К. С. Колесников, Ю. С. Саратов. М.; Изд-во МГТУ им. Н.Э. Баумана, 2001

7. Ильин М.М. Теория колебаний: учебник для вузов/ М.М. Ильин, К.С. Колесников, Ю.С. Саратов; под общ. ред. К.С. Колесникова; Фед. целевая программа "Гос. поддержка интеграции выс. образ. и фундаментальной науки. М.; Изд-во МГТУ им. Н.Э. Баумана, 2003

8. Каннингхэм В. Введение в теорию нелинейных систем. М.-Л., ГЭИ, 1962.

9. Леденев, Александр Николаевич.Физика. В 5-ти кн.: учебное пособие для вузов/ А.Н. Леденев. -М.: Физматлит Кн. 4: Колебания и волны. Оптика, 2005

10. Мандельштам Л.И. Лекции по теории колебаний. М., Наука,1972.

11. Основы теории колебаний: учебное пособие/ В.В. Мигулин, В.И. Медведев, Е.Р. Мустель, В.Н. Парыгин; под ред. В.В. Мигулина. М., Наука,1978.

12. Основы теории колебаний: учебное руководство/ В.В. Мигулин, В.И. Медведев, Е.Р. Мустель, В.Н. Парыгин; под ред. В.В. Мигулина. М., Наука,1988.

13. Обморшев А.Н. Введение в теорию колебаний. М., Наука,1965.

14. Стрелков С.П. Введение в теорию колебаний. М., Наука,1964.

оглавление

ВВЕДЕНИЕ. 3

Математический маятник как модель физического маятника. 7

Идеальный контур как модель реального колебательного контура. 9

Глава 1.СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ КОНСЕРВАТИВНОЙ СИСТЕМЕ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ (ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР) 14

Глава II. СВОБОДНЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ НЕКОНСЕРВАТИВНОЙ СИСТЕМЕ. 19

Энергетические соотношения в системе с малым затуханием. 26

Глава III. МЕТОД ФАЗОВОЙ ПЛОСКОСТИ.. 29

Особая точка типа центр. 35

Особая точка типа фокус. 37

Особая точка типа узел. 45

Самовозбуждение RC – генератора. 50

Особая точка типа седло. 52

Глава IV.СВОБОДНЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНОЙ КОНСЕРВАТИВНОЙ СИСТЕМЕ. 57

Глава V.СВОБОДНЫЕ КОЛЕБАНИЯ В СИСТЕМЕ С КУЛОНОВСКИМ ТРЕНИЕМ 64

Фазовый портрет системы с кулоновским трением. 69

Глава VI. Устойчивость равновесия системы.. 73

Устойчивость состояния равновесия линейной системы с одной степенью свободы 75

Устойчивость равновесия линейной системы с N степенями свободы.. 80

Исследование устойчивости состояния равновесия нелинейной системы по первому приближению (второй метод Ляпунова) 85

Глава VII. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В СИСТЕМАХ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ (ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ) 95

Глава VIII. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ.. 98

Колебания в линейной консервативной системе при включении источника гармонических колебаний. 103

Гармонический осциллятор при произвольном внешнем воздействии. 108

Литература. 111