Глава VI. Устойчивость равновесия системы

Важным этапом исследования колебательных систем является исследование устойчивости какого-либо состояния в системе: состояния устойчивости, стационарного колебания и т.п. сосредоточим свое внимание на исследовании устойчивости состояния равновесия, так как этот случай встречается в подавляющем большинстве практических задач.

Какое состояние считать устойчивым? На основе опыта мы говорим, что система устойчива, если выведенная из какого-либо состояния она стремится вернуться в это состояние.

Поэтому исследование устойчивости состояния эквивалентно решению вопроса реализуемости этого состояния. Если состояние устойчиво – оно реализуемо. Интуитивное определение устойчивости не может служить основой для строгого анализа устойчивости систем.

Фундаментальные результаты по теории устойчивости были получены русским математиком А.М. Ляпуновым в конце прошлого века. Некоторые будут изложены ниже.

Дадим математическую формулировку устойчивости состояния равновесия системы.

Пусть система описывается координатами, меняющимися во времени 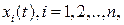и пусть 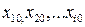-состояние равновесия системы. (В состоянии равновесия все скорости равны нулю: 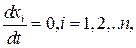-движение отсутствует).

1.Состояние равновесия устойчиво по Ляпунову, если для любого положительного 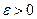можно указать такое положительное 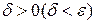, что в любой момент времени выполняется условие

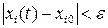, (6.1)

если в начальный момент 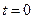выполняется условие

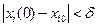. (6.2)

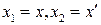Устойчивость по Ляпунову легко проиллюстрировать на фазовой плоскости . Нарисуем два квадрата со сторонам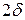и и 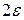с центром в состоянии равновесия (Рис.41).

Устойчивость по Ляпунову означает, что фазовая траектория, начавшаяся внутри малого квадрата, никогда не выйдет за пределы большого квадрата. Причем большой квадрат задается, а малый должен существовать.

Физически устойчивость по Ляпунову означает, что система не обязательно достигает своего состояния равновесия, но и не уходит от него; она может совершать движение около своего состояния равновесия сколько угодно долго. Конкретным примером равновесия, устойчивого по Ляпунову, может служить особая точка типа центр (Рис.42).

При заданном 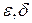равно малой полуоси эллипса, большая полуось которого равна 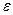. Очевидно, что при начальных условиях, расположенных внутри квадрата 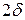, траектории представляют эллипсы, которые находятся внутри квадрата .

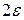В прикладных задачах чаще приходится исследовать асимптотическую, или, абсолютную устойчивость состояния равновесия.

Состояние равновесия 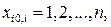абсолютно устойчиво, если можно указать такое положительное число 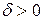, что при выполнении в начальный момент времени условия

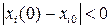, (6.3)

Справедливо

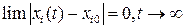. (6.4)

Физический смысл этого условия очевиден: если отклонение системы не превышает некоторого значения, то система через достаточно большой промежуток времени переходит в состояние равновесия.

В качестве конкретного примера можно привести колебательный контур с потерями. Как было показано выше, при наличии потерь в колебательном контуре выходное колебание имеет вид затухающей синусоиды, т.е. при любых начальных условиях система всегда возвращается в исходное состояние. Состояние равновесия абсолютно устойчивое устойчиво и по Ляпунову. Обратное утверждение несправедливо. Требования для выполнения абсолютной устойчивости более жесткие, чем для устойчивости по Ляпунову.