Фазовый портрет системы с кулоновским трением
Рассмотрим систему с кулоновским трением, используя метод фазовой плоскости. На этом примере можно проиллюстрировать, как хорошо сочетается метод фазовой плоскости и метод сшивания.
Найдем фазовый портрет системы с сухим трением. Уравнение системы (5.39)
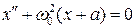 при
при 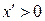 ,
,
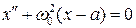 при
при 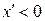 . (5.39)
. (5.39)
Повторим выкладки, которые имели место для гармонического осциллятора, получим уравнения фазовых траекторий
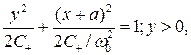
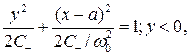 (5.40)
(5.40)
где 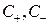 - константы, определяемые из начальных условий.
- константы, определяемые из начальных условий.
 Видно (Рис.37), что фазовые траектории рассматриваемой системы составлены из половин эллипсов, причем в верхней полуплоскости центры эллипсов расположены в точке (_а, 0), а в нижней – в точке (а, 0). Нетрудно построить фазовую траекторию, соответствующую определенному начальному условию, если воспользоваться методом сшивания.
Видно (Рис.37), что фазовые траектории рассматриваемой системы составлены из половин эллипсов, причем в верхней полуплоскости центры эллипсов расположены в точке (_а, 0), а в нижней – в точке (а, 0). Нетрудно построить фазовую траекторию, соответствующую определенному начальному условию, если воспользоваться методом сшивания.
Пусть точка 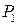 является начальной через нее проходит эллипс с центром в (-а,0). Изображающая точка должна двигаться по нему слева направо. В точке
является начальной через нее проходит эллипс с центром в (-а,0). Изображающая точка должна двигаться по нему слева направо. В точке 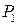 у=0, скорость меняет знак и дальнейшее движение должно описываться эллипсом, центр которого в (+а,0). Точка
у=0, скорость меняет знак и дальнейшее движение должно описываться эллипсом, центр которого в (+а,0). Точка 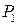 является для него начальной. Очевидно, что в точке
является для него начальной. Очевидно, что в точке 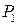 сшиваются две разные траектории. Двигаясь по дуге
сшиваются две разные траектории. Двигаясь по дуге 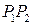 , приходим в точку
, приходим в точку 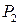 , где скорость вновь меняет знак. Точка
, где скорость вновь меняет знак. Точка 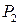 является начальной для эллипса в верхней полуплоскости и т.д. Движение прекращается, когда изображающая точка попадает на отрезок
является начальной для эллипса в верхней полуплоскости и т.д. Движение прекращается, когда изображающая точка попадает на отрезок 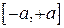 .
.
Взяв другое начальное значение, получим соответствующую фазовую траекторию. В качестве примера возьмем то начальное значение, которое исследовалось аналитически: 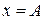 ,
, 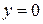 .
.
 Видно, что фазовые траектории имеют вид спиралей, а изображающая точка стремится к состоянию равновесия.
Видно, что фазовые траектории имеют вид спиралей, а изображающая точка стремится к состоянию равновесия.
В заключении проиллюстрируем эффективность метода сшивания на фазовой плоскости на примере исследования свободных колебаний в контуре с диодом. (Рис.38).
Считаем диод идеальным, т.е. он работает как ключ, который замыкает цепь при прямом напряжении и размыкает - при обратном.
При рассмотрении колебаний можно четко выделить два этапа, которым соответствуют две эквивалентные схемы, подробно изученные ранее (Рис.39).
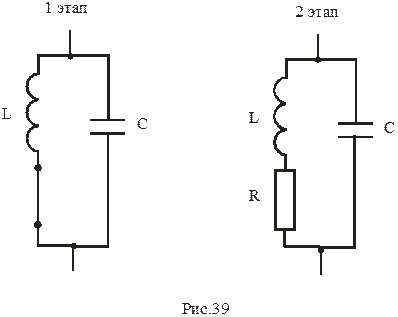
На фазовой плоскости 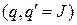 , 1 этап соответствует верхней полуплоскости т фазовые траектории – полуэлипсы; 2 этап соответствует нижней полуплоскости и траектории- отрезки спиралей. При
, 1 этап соответствует верхней полуплоскости т фазовые траектории – полуэлипсы; 2 этап соответствует нижней полуплоскости и траектории- отрезки спиралей. При 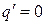 траектории сшиваются.
траектории сшиваются.
Легко видеть, что состоянию равновесия 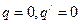 соответствует особая точка типа фокус (Рис.40).
соответствует особая точка типа фокус (Рис.40).

Дата добавления: 2015-01-13; просмотров: 1289;
