Устойчивость состояния равновесия линейной системы с одной степенью свободы
В общем случае такая система описывается двумя уравнениями;
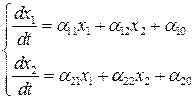 , (6.5)
, (6.5)
все 
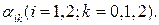 будем считать постоянными и предполагать, что детерминант
будем считать постоянными и предполагать, что детерминант
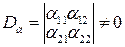 (6.6)
(6.6)
отличен от нуля. Состояние равновесия системы определим из условия:
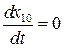 ;
; 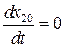 .
.
Тогда
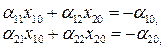 . (6.7)
. (6.7)
Корнями этого алгебраического уравнения служат координаты точек равновесия. Вводят координаты
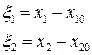 , (6.8)
, (6.8)
которые характеризуют отклонение от состояния равновесия, приведем уравнение (6.5) к виду:
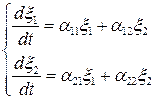 . (6.9)
. (6.9)
Состояние равновесия соответствует началу координат 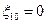 ,
, 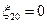 . Для исследования его устойчивости проинтегрируем уравнение (6.9) и, анализируя
. Для исследования его устойчивости проинтегрируем уравнение (6.9) и, анализируя 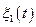 и
и 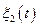 , проследим, куда движется система со временем: к состоянию равновесия или от него.
, проследим, куда движется система со временем: к состоянию равновесия или от него.
Уравнение (6.9) линейное и решение ищем методом Эйлера. Пусть
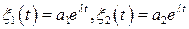 , (6.10)
, (6.10)
где 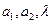 - пока неизвестные постоянные.
- пока неизвестные постоянные.
Подставляя в (6.9) и сокращая на 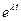 , получим;
, получим;
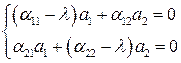 . (6.11)
. (6.11)
Эта система имеет решение  ,
,  только при условии
только при условии
 . (6.12)
. (6.12)
Раскрывая детерминант, имеем
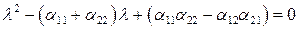 . (6.13)
. (6.13)
Получим характеристическое уравнение системы. Обозначим
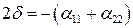 , (6.14)
, (6.14)
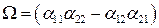 , (6.15)
, (6.15)
тогда характеристическое уравнение примет вид:
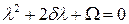 , (6.16)
, (6.16)
Отсюда
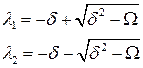 . (6.17)
. (6.17)
Двум значениям  и
и 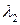 соответствуют два частных решения. Как известно, общее решение записывается как сумма частных;
соответствуют два частных решения. Как известно, общее решение записывается как сумма частных;
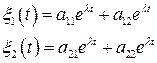 . (6.18)
. (6.18)
Постоянные коэффициенты 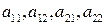 выражаются через
выражаются через 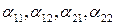 из уравнений (6.7), а сами постоянные
из уравнений (6.7), а сами постоянные 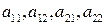 определяются из начальными условиями.
определяются из начальными условиями.
В любую из координат входят экспоненциальные члены, содержащие оба характеристических корня. Посмотрим, как ведут себя координаты при различных  и
и 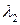 .
.
1. Пусть 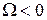 , тогда корни действительные, разных знаков
, тогда корни действительные, разных знаков 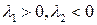 . Условие
. Условие 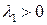 означает, что экспонента
означает, что экспонента 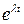 растет. Любая координата при
растет. Любая координата при  уходит в бесконечность (
уходит в бесконечность ( 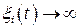 ), т.е. удаляется от точки равновесия. Следовательно, система неустойчива. На фазовой плоскости этот случай соответствует особой точке типа седло.
), т.е. удаляется от точки равновесия. Следовательно, система неустойчива. На фазовой плоскости этот случай соответствует особой точке типа седло.
2. Пусть 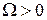 и
и 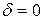 . Тогда корни получаются чисто мнимыми и комплексно-сопряженными
. Тогда корни получаются чисто мнимыми и комплексно-сопряженными
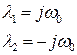 , (6.19)
, (6.19)
где 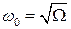 .
.
Решение соответствует периодическим колебаниям
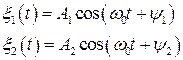 . (6.20)
. (6.20)
Колебания происходят около состояния равновесия, в ограниченной области (устойчивость по Ляпунову). На фазовой плоскости будет особая точка типа центр.
3. Пусть 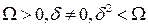 . Получаем два комплексно- сопряженных корня
. Получаем два комплексно- сопряженных корня
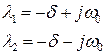 , (6.21)
, (6.21)
где 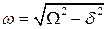 .
.
Решения имеют вид:
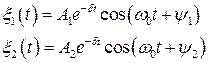 . (6.22)
. (6.22)
Поскольку 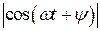 не превышает 1, то поведение
не превышает 1, то поведение 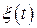 определяется множителем
определяется множителем 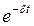 . Если
. Если  , любая из координат стремится со временем к нулю (т.е. состоянию равновесия). На фазовой плоскости равновесию соответствует особая точка типа устойчивый фокус. Состояние равновесия асимптотически устойчиво.
, любая из координат стремится со временем к нулю (т.е. состоянию равновесия). На фазовой плоскости равновесию соответствует особая точка типа устойчивый фокус. Состояние равновесия асимптотически устойчиво.
Если 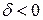 , координата уходит со временем в бесконечность, равновесие неустойчиво (на фазовой плоскости особая точка типа неустойчивый фокус).
, координата уходит со временем в бесконечность, равновесие неустойчиво (на фазовой плоскости особая точка типа неустойчивый фокус).
4. И последний возможный случай 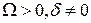 , но
, но 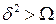 .
.
Корни (6.17) действительные, различные, и знаки определяются знаком 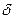 . Если
. Если  , то
, то 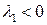 и
и 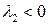 . Это означает, что
. Это означает, что 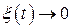 , так как
, так как  при
при 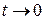 . Состояние равновесия асимптотически устойчиво (соответствует устойчивому узлу).
. Состояние равновесия асимптотически устойчиво (соответствует устойчивому узлу).
Если 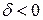 , то
, то 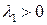 и
и 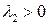 , то
, то 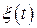 стремится к бесконечности (на фазовой плоскости особая точка типа неустойчивый узел).
стремится к бесконечности (на фазовой плоскости особая точка типа неустойчивый узел).
Подведем итоги. Состояние равновесия линейной системы асимптотически устойчиво, если реальные части корней характеристического уравнения отрицательные 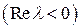 . Для этого (см. 3 и 4) необходимо и достаточно, чтобы коэффициенты характеристического уравнения (6.16) были положительны
. Для этого (см. 3 и 4) необходимо и достаточно, чтобы коэффициенты характеристического уравнения (6.16) были положительны 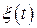
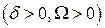 . Если
. Если 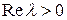 , состояние равновесия неустойчиво. Для этого достаточно, чтобы хоть один из коэффициентов
, состояние равновесия неустойчиво. Для этого достаточно, чтобы хоть один из коэффициентов 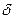 или
или 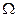 был отрицательным.
был отрицательным.
Если 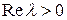 , но
, но 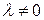 , равновесие устойчиво по Ляпунову.
, равновесие устойчиво по Ляпунову.
Полученные выводы наглядно отображаются на диаграмме особых точек (Рис.43). В качестве осей выбираются значения коэффициентов 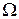 и
и  характеристического уравнения (6.16) линейной системы. Вся плоскость разбивается на области, соответствующие разным типам движения.
характеристического уравнения (6.16) линейной системы. Вся плоскость разбивается на области, соответствующие разным типам движения.
 |
Какие практические выводы следуют из этой диаграммы. Например, невозможно сразу перейти от особой точки типа седло к особой точке типа фокус.
Параметры 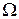 и
и  зависят от конкретных параметров системы. Каждая точка на диаграмме соответствует определенной совокупности реальных параметров.
зависят от конкретных параметров системы. Каждая точка на диаграмме соответствует определенной совокупности реальных параметров.
Центры на диаграмме занимают линию. Для того, чтобы попасть в особую точку типа центр, нужно отдельно подбирать параметры, что практически реализовать невозможно.
В связи с этим вводятся понятия грубой и негрубой системы. Система грубая, если характер движения ее нечувствителен к малому изменению параметров системы (например, колебательный контур с различными, но малыми потерями).
Система негрубая, если тип движения резко меняется при малом изменении параметра. Примером может служить гармонический осциллятор. На практике может реализовываться грубая система.
В заключении, несколько слов о бифуркации.
Бифуркация – это изменение характера движения колебательной системы. На диаграмме особых точек бифуркация соответствует смене типа особой точки. Такая смена происходит при изменении некоторого параметра системы. Соответствующий параметр называется бифуркационным.
Дата добавления: 2015-01-13; просмотров: 1269;
