Колебания в линейной консервативной системе при включении источника гармонических колебаний

На примере этой задачи рассмотрим частный, но важный для практики, случай не стационарного внешнего воздействия, а также уточним вид вынужденных колебаний при резонансном воздействий.

Динамическое уравнение линейной консервативной системы (гармонического осциллятора) при включений источника, при 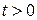, имеет вид:

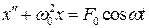. (8.32)

Пусть в момент включения 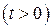система находилась в равновесии:

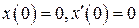. (8.33)

Вследствие нестационарности внешнего воздействия колебания в системе необходимо описывать общим решением (7.6):

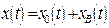. (8.34)

Каждое из слагаемых уже известно: (2.7), (8.29). Тогда общее решение (8.32) имеет будет иметь вид;

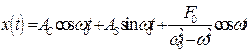. (8.35)

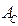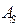Постоянные и определим из начальных условий (8.33);

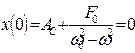, (8.36)

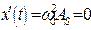. (8.37)

Откуда

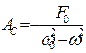, (8.38)

и после подстановки (8.38) в (8.35) принимает вид;

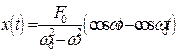. (8.39)

Преобразуя разность косинусов, получим другую форму записи;

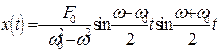. (8.40)

Соответствующие графики приведены на рисунке 47.

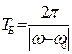. (8.41)

Собственные колебания появились вследствие включения источника. Если бы система обладала затуханием, то через некоторое время (приблизительно время релаксации 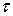) свободные колебания затухли бы и остались только вынужденные. Если 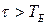, биения после включения можно наблюдать экспериментально.

Особый интерес представляют колебания в осцилляторе при включении гармонического источника с резонансной частотой.

Что бы получить решение при 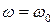, необходимо в (8.40) перейти к пределу. Перепишем (8.40) в виде:

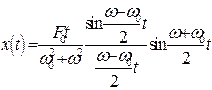. (8.42)

и учитывая, что при выполнении условия

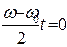. (8.43)

Справедливо следующее выражение

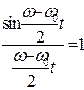. (8.44)

Подставляя (8.44) в (8.42), получим

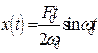. (8.45)

на графике это колебание выглядит так, как показано на рисунке 48.

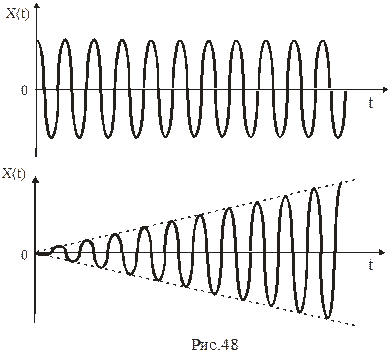
Огибающая амплитуд растет по линейному закону. Важно отметить, что амплитуда вынужденных колебаний бесконечна, через бесконечное время. Отсюда ясно, почему в (8.30) амплитуда бесконечна при 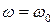. Потому что в методе комплексных амплитуд действие источника предполагается бесконечным во времени.

При конечном времени наблюдения (или действия внешнего источника) амплитуда всегда будет конечной. В частности, при действии прямоугольного радиоимпульса на высокодобротный колебательный контур можно наблюдать процесс, соответствующий линейному росту амплитуды.

Аналогичный результат получим при включении синусоидальной внешней силы:

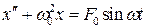. (8.46)

Пусть в момент включения 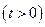система находилась в равновесии;

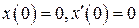, (8.47)

тогда после преобразований рассмотренных выше получим

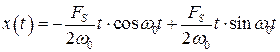. (8.48)

В общем случае, когда на гармонический осциллятор действует резонансная внешняя сила, равная сумме синусоидальных и косинусоидальных составляющих колебание можно записать в форме собственных колебаний с переменными амплитудами

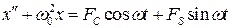, (8.49)

где

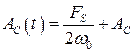, (8.50)

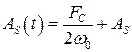. (8.51)

Видно, что косинусоидальное колебание в системе раскачивается синусоидальной внешней силой, а синусоидальное колебание раскачивается косинусоидальной внешней силой. В общем случае в выражение (8.50,8.51) входят постоянные добавки, которые соответствуют свободным колебаниям системы. При достаточно большом времени ими можно пренебречь. Чтобы исключить влияние свободных колебании и внешней силой запишем в дифференциальной форме, которая следует из (8.50,8.51);

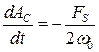, (8.52)

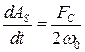. (8.53)

Этим результатом мы воспользуемся в будущем при обосновании энергетического метода, когда будем анализировать нелинейные системы.