Оценки среднего ресурса системы по ресурсу элементов
| Функция распределения ресурса i -того элемента | Точечная оценка ресурса | Нижняя доверительная граница ресурса при доверительной вероятности q | Примечание |
| Экспоненциальный | 
| 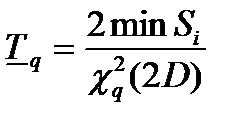
| 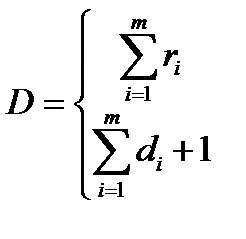
|
| Возрастающая функция интенсивности отказов | 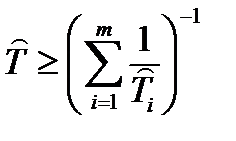
| 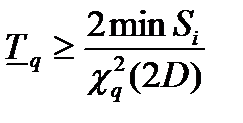
| |
| Произвольный | 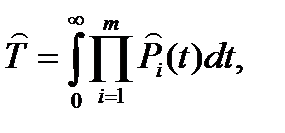
| 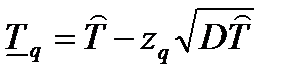
| 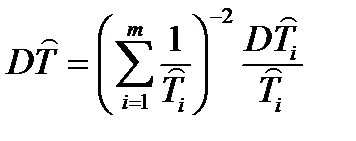
|
Здесь: zq – квантиль распределения вероятности q, т.е. значение аргумента, при котором функция распределения принимает значение, равное q (при нормальном законе распределения квантиль распределения обычно обозначают буквой u); DT – дисперсия точечной оценки ресурса системы.
Таблица 25
Оценка гамма – процентного ресурса системы
| Функция распределения ресурса i -того элемента | Точечная оценка ресурса | Нижняя доверительная граница ресурса при доверительной вероятности q | Примечание |
| Экспоненциальный | 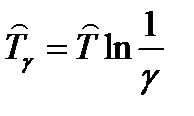
| 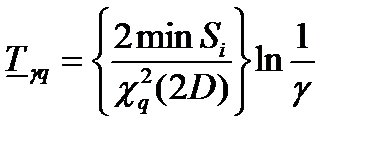
| Si – суммарная наработка |
| Возрастающая функция интенсивности отказов | 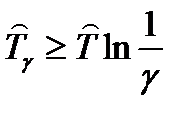
| 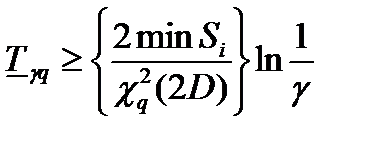
| |
| Произвольный | 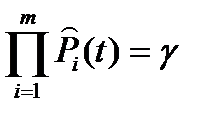 * *
| 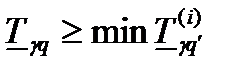
| 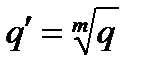
|
Примечание: * - точечная оценка ресурса является корнем этого уравнения.
ПРИМЕР 33
Имеется система из m=3 независимых последовательно соединенных элементов. Каждый элемент имеет стареющее распределение ресурса (возрастающая функция интенсивности отказов – ВФИ – распределение). В результате испытаний по плану [NiUri] получено: S1=60 часов, ri=4; S2=50 часов, r2=5; S3=100 часов, r3=2. Найти точечные оценки среднего ресурса системы, гамма – процентного ресурса при γ = 0,8 и нижние доверительные границы этих показателей при доверительной вероятности q = 0,9.
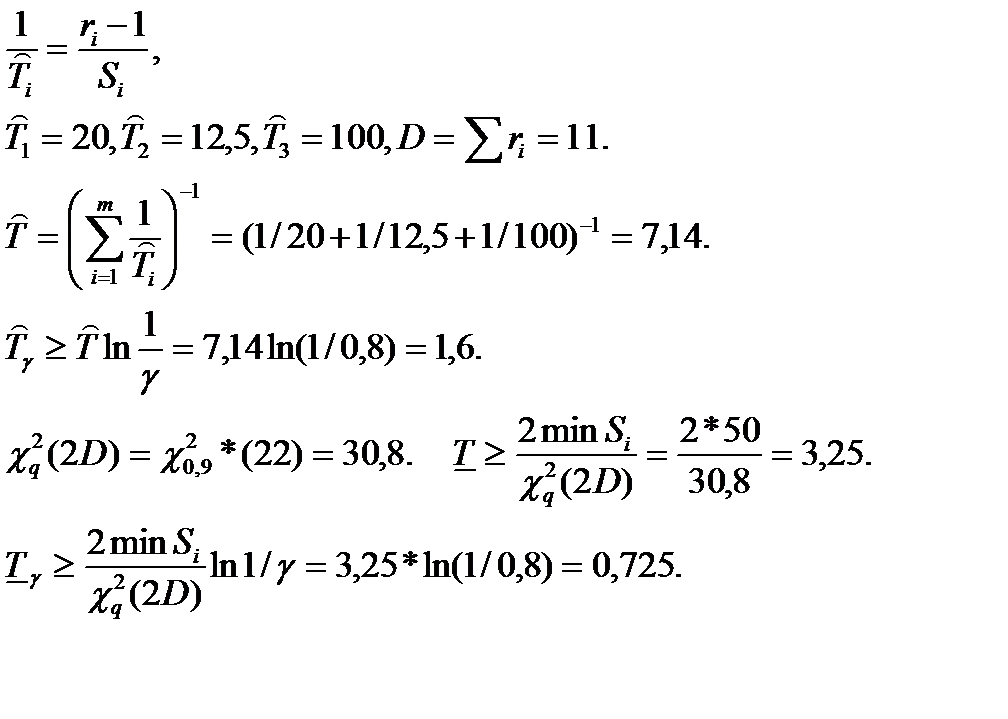
Дата добавления: 2015-03-19; просмотров: 955;
