Один контрольный уровень

Испытания по этому плану могут проводиться на N₀ образцах или на одном образце, при условии, что в процессе испытаний образца не производятся воздействия, влияющие на его надёжность (накопление повреждений, восстановление, доработка и пр.). Биномиальный план обладает наибольшей общностью, но и требует больших объемов испытаний для подтверждения высоких требований по надежности. Сокращение объема испытаний возможно при их форсировании или учете коэффициента функциональной избыточности системы u. Число образцов для испытаний при биномиальном плане на интервале времени [0,t₀] в номинальном режиме без утяжеления определяется по соотношению:

N₀=lnβ/lnP_норм

при допустимом числе отказов l_доп=0 или при допустимом числе отказов l_доп>0 по соотношению:

N₀=minN, определяемого из неравенства

f₂(N,l_доп,1-β)≥P_норм,

где f₂ - табулированная функция биномиального распределения (функция Клоппера – Пирсона), характеризующая нижнюю доверительную границу вероятности безотказной работы при уровне доверия (1-β).

При коэффициенте функциональной избыточности u > 0 значение нормируемого показателя P_норм в расчетных соотношениях заменяют на отношение: (P_норм - u)/(1 - u).

Структурная избыточность определяется числом ребер неориентированного связного графа с n вершинами по отношению к минимально необходимому:

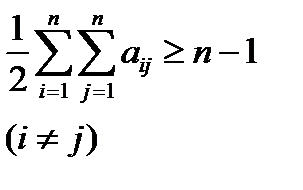
Коэффициент структурной избыточности определяется по формуле:

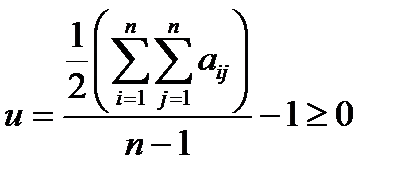
При биномиальном плане испытаний при тех же допущениях, но с остановкой, объем выборки определяют по соотношениям:

N₀=β^-1-1 при l_доп=0,

N₀=2β^-1-1 при l_доп=1.

План испытаний с остановкой отличается от обычного биномиального плана тем, что в нем испытания ведутся последовательно в заданном интервале времени, а не одновременно, и на планируемый объем испытаний не накладываются ограничения по постоянству показателя надежности.

ПРИМЕР 34

Задано требуемое значение вероятности безотказной работы системы P_норм=0,9 на интервале [0,t₀] в номинальном режиме, при допустимом риске потребителя β = 0,1, при l_доп=0 и l_доп=1. Определить требуемый объем испытаний при биномиальном плане.

Для случая без отказов N₀=lnβ/lnP_норм=ln0,1/ln0,9=22. Для случая с одним отказом N₀ находим из неравенства f₂(N,l_c,1-β)≥P_норм с помощью табл.2 Приложения [4Т, том 6] N₀=22.

Примечание: Если бы мы задали более высокий уровень надежности, например, P_норм=0,99, то, при том же риске потребителя, объем испытаний для двух рассматриваемых случаев (без и с отказом) был бы существенно различным: 229 и 300 образцов соответственно.