Контроль наработки. Одноступенчатый план контроля наработки П1(ТΣ, с) заключается в определении нормативов суммарной наработки ТΣ и отказов с для известного
Одноступенчатый план контроля наработки П1(ТΣ, с) заключается в определении нормативов суммарной наработки ТΣ и отказов с для известного распределения контролируемого показателя и заданных рисках.
Оптимальным планом при контроле наработки является план типа [NUN]. Все образцы испытывают до отказа. В отличие от контроля безотказности, для планирования контроля наработки должен быть известен вид закона распределения показателя надежности. При двух контрольных уровнях условия приемки следующие: при суммарном числе отказов rΣ(TΣ)≤c и Т=Тпр принимается нулевая гипотеза (партия принимается), при rΣ(TΣ)≥(c+1) и Т=Тбр нулевая гипотеза отвергается (партия бракуется).
Оперативная характеристика плана при экспоненциальном законе распределения определяется соотношением:
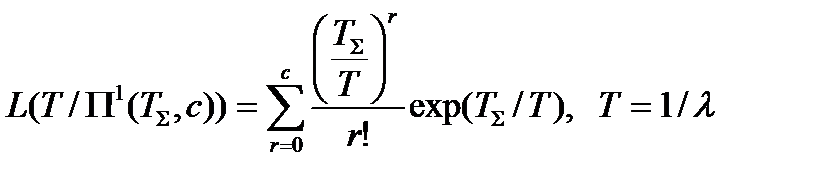 .
.
В табл. 28 приведены планы контроля наработки при экспоненциальном законе распределения. По заданным отношению Тпр/Тбр (T0/T1) и рискам определяют норматив суммарной наработки и числа отказов.
Таблица 28
Одноступенчатые планы контроля наработки
| Т0/Т1 при β= | r | ТΣ/Т0 | ||
| 0,05 | 0,10 | 0,20 | ||
| α=0,05 | ||||
| 58,820 | 45,450 | 31,250 | 0,052 | |
| 13,330 | 10,990 | 8,403 | 0,356 | |
| 7,692 | 6,493 | 5,235 | 0,817 | |
| 4,651 | 4,065 | 3,413 | 1,970 | |
| 3,646 | 3,205 | 2,762 | 3,285 | |
| 2,898 | 2,618 | 2,309 | 5,425 | |
| 2,369 | 2,178 | 1,961 | 9,246 | |
| 2,096 | 1,961 | 1,779 | 13,200 | |
| 1,942 | 1,815 | 1,669 | 17,300 | |
| 1,835 | 1,721 | 1,597 | 21,500 | |
| α=0,10 | ||||
| 28,570 | 21,740 | 15,380 | 0,105 | |
| 8,928 | 7,299 | 5,650 | 0,532 | |
| 5,714 | 4,831 | 3,891 | 1,102 | |
| 3,769 | 3,289 | 2,762 | 2,432 | |
| 3,039 | 2,703 | 2,331 | 3,895 | |
| 2,525 | 2,283 | 2,012 | 6,221 | |
| 2,127 | 1,953 | 1,760 | 10,300 | |
| 1,915 | 1,792 | 1,626 | 14,520 | |
| 1,792 | 1,672 | 1,538 | 18,840 | |
| 1,706 | 1,602 | 1,489 | 23,230 |
Количество образцов для испытаний может быть различным и может быть определено разными способами. Если при планировании испытаний пользоваться табл. 28, тогда, при испытаниях без восстановления и замены отказавших образцов, число образцов должно быть не менее значения r из табл. 28. При испытаниях с восстановлением или заменой объем выборки может быть любым, лишь бы была достигнута заданная суммарная наработка. В тех случаях, когда дополнительно задана продолжительность испытаний Tисп, а отказавшие образцы восстанавливаются или заменяются, объем выборки определяют по отношению: TΣ/Tисп. При невосстанавливаемых и не заменяемых образцах объем испытаний следует увеличить на TΣ/Tпр образцов (если, разумеется, это отношение больше единицы).
Объем выборки может быть определен иначе – по таблицам χ2 – распределения с учетом того, что из равенства приемочного и браковочного уровней:
Tпр=(T1/2N)χ2β (2N) и Tбр=(T0/2N)χ21-α(2N)
следует, что
T0/T1=χ2β(2N)/χ21-α(2N).
В этом случае заданы контрольные уровни средней наработки T0 и T1. Число образцов N определяют из таблиц по коэффициенту k=2N (k – левый столбец таблицы критерия Пирсона). После определения объема выборки уточняется приемочный уровень для средней наработки: Tпр=(T1/2N)χ2β (2N). Он будет несколько отличаться от T0.
ПРИМЕР 35
Заданы значения рисков потребителя и поставщика α=β=0,10, контрольные уровни средней наработки для принятия нулевой T0=100ч и альтернативной T1=67ч гипотез. Распределение наработки экспоненциальное. Необходимо провести планирование испытаний, т.е. определить объем испытаний N и уточнить приемочный уровень средней наработки Tпр.
По таблицам ХИ – квадрат распределения попарным подбором квантилей в столбцах с вероятностями 1-α=0,90 и β=0,10 добиваемся выполнения равенства:
χ2β(2N)/χ21-α(2N)=T0/T1=100/67=1,5. Оно выполняется при χ20,10=98,7 и χ20,90=66,01. При этом k=2N=82, следовательно N=41 образец. Приемочное значение средней наработки равно:
Tпр=(T0/2N)χ21-α(2N)=(100/82)66,01=80,5ч. или, что то же самое,
Tпр=(T1/2N)χ2β(2N)=(67/82)98,7=80,5ч
С практической точки зрения испытания удобнее и проще вести по контрольному значению числа отказов (т.е. с использованием табл. 28), чем по нормативу средней наработки.
Планирование контрольных испытаний при других законах распределения наработки подробно нами не рассматривается.
Дата добавления: 2015-03-19; просмотров: 1156;
