Контроль безотказности
При контроле вероятности безотказной работы Р за наработку t0 условия принятия нулевой и альтернативной гипотез следующие: Н0: Рфакт(t0)=Р0(t0) и Н1: Рфакт(t0)=Р1(t0).
В общем случае вероятность появления r отказов в выборке объемом n описывается гипергеометрическим распределением. Из этого, в конечном итоге, следует, что критерий правдоподобия может быть определён из выражения:
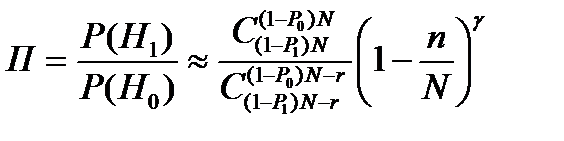 ,
,
где r – число отказов;
N – объем партии;
n - объем выборки испытаний;
γ = N(P0-P1).
Биномиальный коэффициент (число сочетаний из n по k) равен:
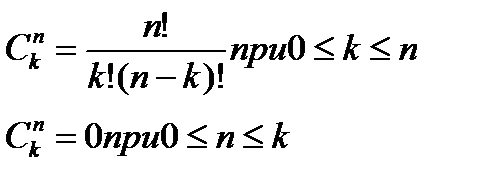
Линии браковки и приемки строят на графике r(n) по трем точкам (треугольник): две на оси абсцисс с координатами:
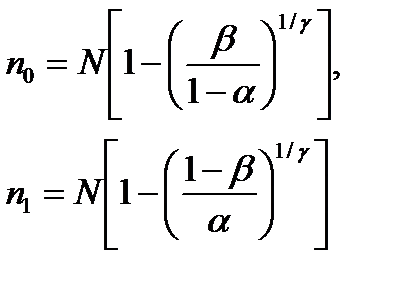
и одна – с координатами (N,rc), где rc=N(2-P0-P1)/2.
При n<0,1N вероятность появления отказов в выборке n описывается биномиальным распределением и критерий правдоподобия определяется по соотношению:
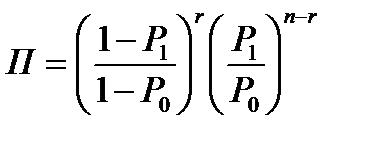 .
.
Для упрощения планирования испытаний разработаны таблицы, по которым строятся линии приемки и браковки в виде прямых в координатах (r,n):
r=a(n-n0) – линия приемки;
r=an+r0 – линия браковки.
Где:
a=(lnP0/P1)/[ln((1-P1)/(1-P0))+ln(P0/P1)],
r0=ln((1-β)/α))/[ln((1-P1)/(1-P0))+ln(P0/P1)],
n0=ln((1-α)/β))/ln(P0/P1).
На рис. 24 показан пример построения плана и хода успешного и неуспешного испытаний на безотказность.
| 0 n0 50 100 n |
| r r0 |
| II |
| I |
| Рис.24. График контроля хода испытаний на безотказность: 1, 2 – линии приёмки и браковки; I, II – положительный и отрицательный варианты реализации испытаний; Н0, Н1 – области правомерности гипотез |
| Н1 |
| Н0 |
Дата добавления: 2015-03-19; просмотров: 850;
