Экспоненциальном законе распределения

Тип ССН; условия приёмки	Число требуемых образцов ι–го типа	Примечание
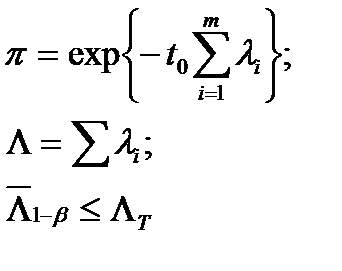
Последовательная;		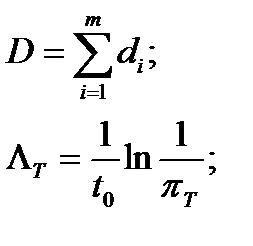t0 – заданная наработка
Параллельная;

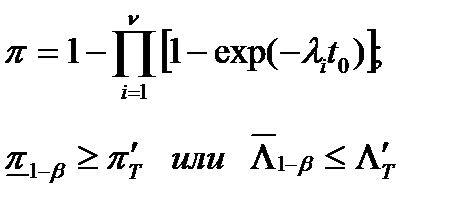
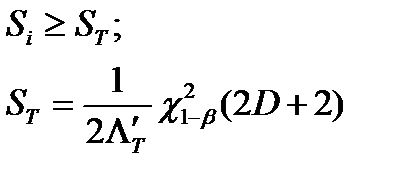
В заключение раздела рассмотрим несколько примеров планирования испытаний системы с последовательной и параллельной ССН.

ПРИМЕР 37

Имеется система с m=10 последовательными разнотипными элементами надежности. Требуемая вероятность безотказной работы π_Т=0,90; допустимый риск заказчика β=0,2. Допускается один отказ в ходе испытаний всех элементов. Требуется определить объем испытаний N_i для элементов каждого типа в испытаниях по биномиальному плану [N_i,U,t₀].

Согласно заданным условиям D=1. По табл. 29 и таблице ХИ - квадрат распределения находим: χ²_0,8(4)=6, N_T=29. Т.е. для каждого элемента требуется провести 29 испытаний. Если бы требуемое число отказов равнялось нулю, тогда бы N_T=ln0,2/ln0,9=15,27≈16.

ПРИМЕР 38

Для системы с последовательной ССН при заданном риске потребителя β=0,10, числе элементов системы m=3, заданных (требуемых) вероятностях безотказной работы элементов P_i 0,80, 0,90 и 0,99 и нулевом числе допустимых отказов определить требуемое количество испытаний элементов N_T по биномиальному плану.

Для системы с последовательной ССН при нулевом числе допустимых отказов по формулам табл. 29 находим:

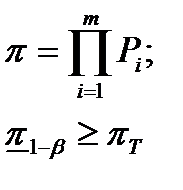
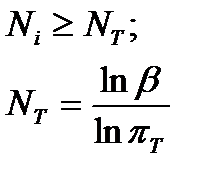
N_T=6,8 (7).

ПРИМЕР 39

Для систем с параллельной ССН при заданном риске потребителя β=0,10, числе элементов системы ν=2, заданных (требуемых) вероятностях безотказной работы элементов Pi 0,90 и 0,99 и нулевом числе допустимых отказов определить требуемое количество испытаний элементов по биномиальному плану.

РЕШЕНИЕ: Для системы с параллельной ССН при нулевом числе допустимых отказов по формулам табл. 7.22 находим:

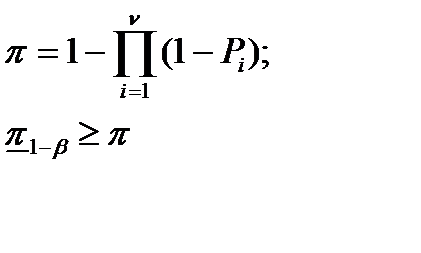
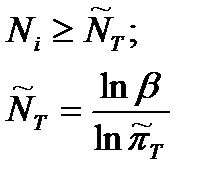
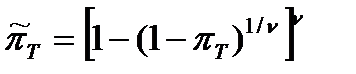
N_T=35,9 (36).