С последовательной ССН при биномиальных испытаниях
ПРИМЕР 31
Система состоит из m последовательно соединенных элементов, вероятность безотказной работы каждого из которых Pi неизвестна. Отказы элементов независимы. Каждый i-ый элемент как бы проходит Ni автономных испытаний по биномиальному плану, с регистрацией числа отказов li. Испытания проходят в номинальном режиме без остановок. По результатам испытаний каждого элемента требуется найти γ - нижнюю границу 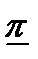 для вероятности безотказной работы системы на интервале времени [0,t0], т.е. для заданной доверительной вероятности γ должно выполняться неравенство: P(
для вероятности безотказной работы системы на интервале времени [0,t0], т.е. для заданной доверительной вероятности γ должно выполняться неравенство: P( 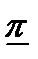 )≥γ.
)≥γ.
Даже при таких, упрощенных условиях, решение задачи неоднозначно. Рассмотрим один из вариантов решения:
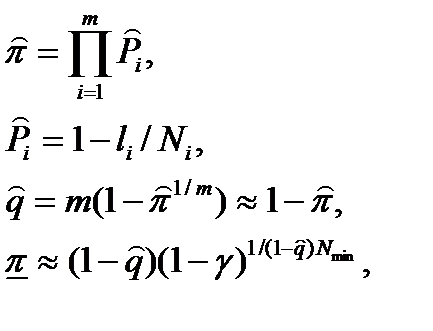
где Nmin – минимальное число испытаний из всех Ni.
Пусть задано: m=3, Ni=10 (для всех элементов), li=2 (для всех элементов). γ =0,8.
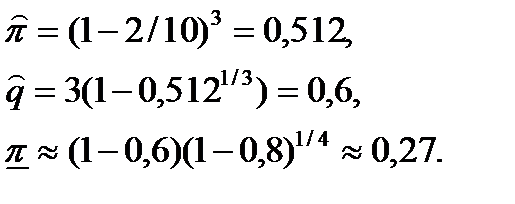
Дата добавления: 2015-03-19; просмотров: 806;
