Оценка показателей безотказности систем с последовательной ССН

при планах испытаний с измерением наработки до отказа

В данном случае известны план испытаний и вид закона распределения (или его класс) наработки до отказа i–того элемента. Из всех возможных ситуаций рассмотрим наиболее «определимую», а именно: все элементы испытываются по одному и тому же плану, закон распределения показателей безотказности для всех элементов один и тот же, неизвестны лишь его параметры, есть данные о наработках до отказа или цензурирования каждого из элементов системы.

По этим данным оценивают неизвестные параметры закона распределения наработки до отказа каждого элемента, а затем находят точечные и интервальные оценки вероятности безотказной работы системы с последовательной ССН.

Рассмотрим случай экспоненциального закона распределения наработки до отказа. При этом выберем наиболее простую систему – систему, состоящую из n последовательно соединённых однотипных элементов (типовая ситуация ТС-1). Вероятность безотказной работы такой системы определяется выражением:

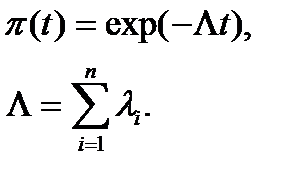
Точечные и интервальные оценки вероятности безотказной работы системы находят по соотношениям:

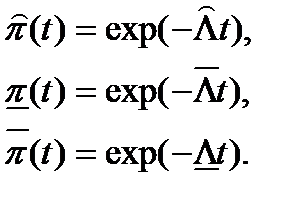
Точечные и интервальные оценки параметра Λ находят по формулам, приведённым в табл. 23.

Таблица 23

Оценки параметра Λ

План испытаний	Точечная оценка	Доверительная граница	Примечание
нижняя	верхняя
[NiUTi]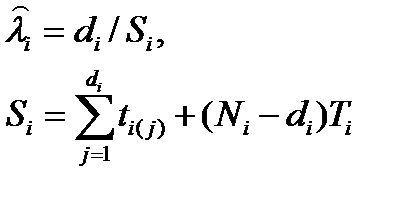
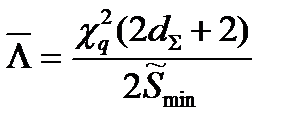
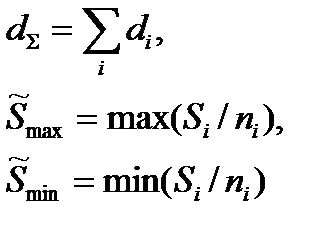
[NiUri]
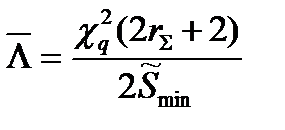
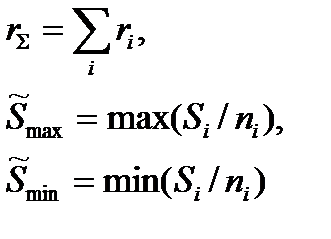
[NiUzi]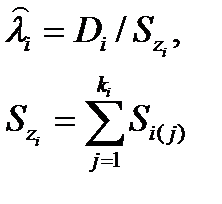

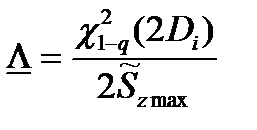
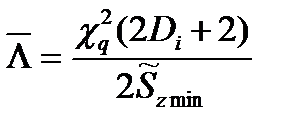
Примечание: При одной группе однородных элементов n_i = 1.

ПРИМЕР 32

Система состоит из последовательно соединенных однотипных элементов (типовая ситуация ТС-1). Вычислить оценки вероятности безотказной работы (точечную и доверительные границы при доверительной вероятности 0,9) при исходных данных:

- число последовательных элементов в системе n = 2;

- испытания элементов проведены по плану [N_iUT_i];

- для 1-го элемента проведено 5 испытаний до наработки 10 часов, зафиксировано 2 отказа после наработок 5 и 7 часов;

- для 2-го элемента проведено 8 испытаний до наработки 10 часов, зафиксировано 3 отказа после наработок 5, 6 и 9 часов;

- закон распределения экспоненциальный;

- наработка для оценки показателя надёжности t₀ = 10 часов.

S1=5+7+10(5-2)=42 часа, λ1=2/42=0,0476, S2=5+6+9+10(8-3)=70 часов, λ2=3/70=0,0429,

=0,0476+0,0429=0,0905.

Для q = 0,9 и d_Σ = 2+3=5 по таблицам для квантилей χ² - распределения находим:

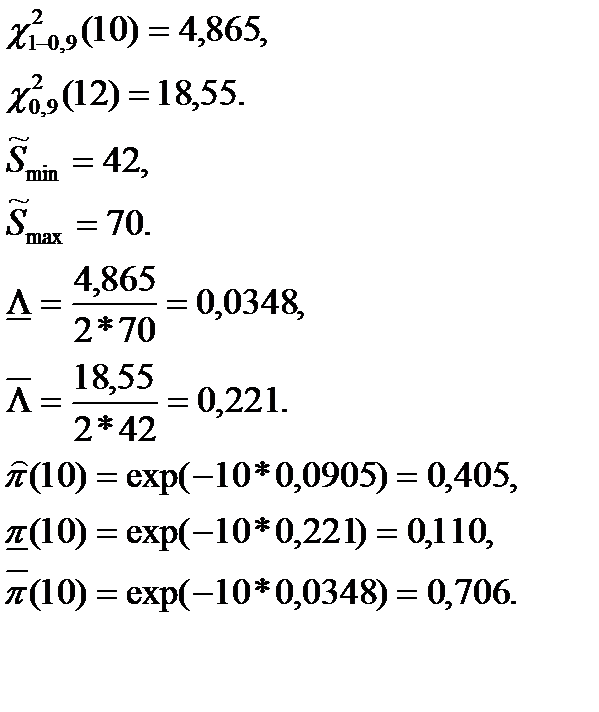
Оценки показателей безотказности систем с разнотипными элементами, другими типовыми ситуациями и иными законами распределения подробно рассмотрены в справочниках.