Метод последовательной смены стационарных состояний

В связи со сложностью точных решений были приложены различные приближенные методы решения задач неустановившейся фильтрации упругой жидкости. Одним из наиболее распространенных приближенных методов является метод последовательной смены стационарных состояний. Метод заключается в том, что в какой то момент времени зона пониженного давления (возмущенная зона) считается распространенной на определенное расстояние l=l(t) (приведенный радиус влияния) и предполагается так, как будто движение жидкости установившееся. В действительности же распределение давления в пласте не будет стационарным и зона пониженного давления захватит теоретически весь пласт. Закон изменения во времени приведенного радиуса влияния l(t) определяется из условия материального баланса. При неустановившемся притоке упругой жидкости к галерее 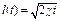, если отбор проводится при постоянной депрессии 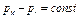; 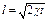, если задан постоянный дебит

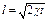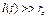При плоскорадикальном притоке упругой жидкости к скважине можно считать с точностью до 10-15%, что (если ) как для случая постоянной депрессии, так и для постоянного отбора.

В методе А.М. Пирвердяна эпюра давления задается так, чтобы она не имела угловых точек. Например, при притоке к галерее распределение давления по пласту задается в виде параболы, касательная к которой в точке х=l(t) горизонтальна (рис. 4.23).

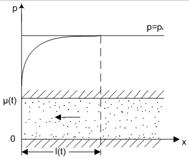
Рис. 4.23. Распределение давления в пласте

Если отбор жидкости не меняется с течением времени, т.е.

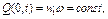
то

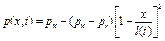(4.126)

где

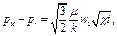(4.127)

а приведенный радиус влияния, найденный из уравнения материального баланса, определяется по формуле

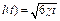(4.128)