Раздел 2. ОСНОВЫ ТЕОРИИ ФОРМИРОВАНИЯ КРИСТАЛЛИЧЕСКОЙ СТРУКТУРЫ ОТЛИВОК 1 страница

Среди литейных процессов центральное место занимает пере­ход сплава из жидкого в твердое кристаллическое состояние. Этот процесс является фазовым переходом первого рода, связанным с изменением объема, теплосодержания и энтропии. При рассмот­рении данного процесса можно выделить два аспекта: количест­венный и качественный. Количественный аспект составляет содер­жание теории затвердевания, главной задачей которой является разработка методов расчета кинетики выделения твердой фазы в объеме расплава. Качественный аспект направлен на рассмот­рение вопросов формирования кристаллической структуры отли­вок и методов управления ею.

ГЛАВА 2.1. ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ САМОПРОИЗВОЛЬНОЙ КРИСТАЛЛИЗАЦИИ МЕТАЛЛОВ И СПЛАВОВ

Современная теория формирования кристаллической структуры отливок .создана за последние 20 лет на основе творческого рас­пространения элементарной теории кристаллизации металлов и сплавов на большие объемы неизотермически затвердевающих расплавов.

Жидкий металл переходит в твердое состояние в соответствии с общими законами термодинамики. Как известно, самопроиз­вольно протекают те процессы, в которых уменьшается свободная энергия и энергия Гиббса G. На рис. 2.1 приведены кривые изменения энергии Гиббса твердого и жидкого металла в зависи­мости от изменения температуры. Видно, что при температуре, большей Т_пл, G_ж < G_тв и устойчивым является жидкое состояние металла. При T < T_пл G_тв < G_ж, поэтому устойчивым является твердое состояние. Температура Т = T_пл, при которой G_тв = G_ж, называется температурой плавления. При равновесном процессе перехода из жидкого состояния в твердое эта температура соот­ветствует равновесной температуре кристаллизации сплава T_кр. "При снижении температуры ниже Т_кр возникает переохлаждение ΔT = T_кр — Т. Так как при этом G_ж > G_тв, то создаются термоди­намические предпосылки для перехода из жидкого состояния в твердое, т. е. для кристаллизации. Движущей силой этого процесса будет разность энергий Гиббса ΔG = G_ж — G_тв. Преобразу­ем это выражение, прибавив и отняв энергии Гиббса жидкой и твердой фаз при T = Т_кр.

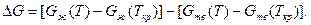
Так как G_ж(Т_кp) = G_тв(Т_кр), то равенство при этой операции не нарушится. Поскольку реальные переохлаждения металлов не ­ велики, то для стоящих в квадратных скобках выра-

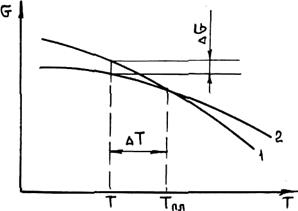
Рис. 2.1. Зависимость энергии Гиббса жидкого (/) и твердого (2) металла от температуры

жений можно написать следующие приближенные равенства:

,

.

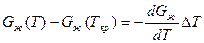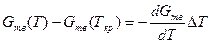С учетом этого ΔG = —ΔТ(dG_ж/dТ — dG_тв/dТ). Так как dG/dТ = —S, то ΔG = +ΔT×ΔS, где ΔS — изменение энтропии при плавлении металла. Как известно, ΔS = L/T_пл, где L— молярная теплота плавления, следовательно, ΔG = L×ΔT/Г_кр. Из этого вы­ражения видно, что с ростом переохлаждения движущая сила кристаллизации увеличивается.

Следует отметить, что при кристаллизации возникает новая фаза, имеющая физическую поверхность раздела с жидкостью. Поэтому кристаллизация связана с затратами энергии на обра­зование и рост данной поверхности раздела фаз. Величина этой энергии равна E_s = s_к-ж×S, где s_к-ж — межфазная энергия на границе раздела фаз; S — поверхность растущего кристалла. В результате образования кристалла объемом V с поверхностью S энергия системы уменьшится на величину ΔG_v и увеличится на величину E_s. Поэтому изменение суммарной энергии Гиббса бу­дет равно

,

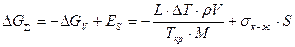где r и М—плотность твердого металла и его молярная масса. Анализ характера зависимости ΔG_å от объема кристалла V пока­зывает, что она имеет экстремальный характер. Характер зависи­мостиΔG_å от радиуса зародыша показан на рис. 2.2.

Кис. 2.2. Зависимость ΔG_å от радиуса зародыша r при разных температурах (T₁>T₂>T_кр>Т₃>Т₄)

В курсе металловедения получено следующее выражение для критического размера сферического зародыша, обеспечивающего максимум ΔG_å (читателю предлагается вывести его самостоя­тельно) :

.

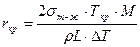Из рис. 2.2 видно, что с понижением температуры, т. е. с уве­личением переохлаждения, радиус критического зародыша стано­вится меньше (r_кр2 < r_кр1). При этом уменьшается и энергия образования критического зародыша.

,

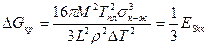где E_sкр — поверхностная энергия зародыша критических размеров.

Пусть по каким-либо причинам в расплаве при данном пере­охлаждении возник зародыш радиуса r < r_кр. Рост такого зародыша (увеличение r), как видно из рис. 2.2, сопровождается рос­том ΔG_å. Поэтому данный зародыш не способен к росту и будет расплавляться. Если радиус зародыша r ³ r_кр, то при присоеди­нении к нему даже одного атома, т. е. с ростом его размеров, ΔG_å будет убывать. Поэтому данный зародыш сможет расти.

Центром кристаллизации будет называться зародыш, обяза­тельно способный к росту. Критический зародыш (r = r_кр) еще не является центром кристаллизации: он может потерять хотя бы одну частицу, т. е. стать дозародышем (r < r_кр) и исчезнуть, или

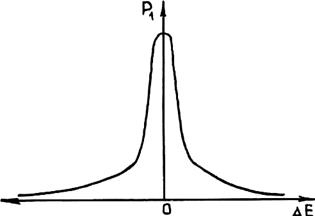
Рис. 2.3. Зависимость вероятности Р₁ флуктуации энергии Е от величины флуктуационного отклонения ΔЕ

присоединить хотя бы одну частицу (r > r_кр) и получить возмож­ность для роста, т. е. стать центром кристаллизации. Поэтому вероятность образования центра кристаллизации равна произве­дению вероятностей образования зародыша критических разме­ров p₁ и присоединения к нему частицы р₂, т. е. p = p₁× p₂.

Вероятность образования центра кристаллизации равна отно­шению числа возникших в единицу времени в единице объема расплава центров кристаллизации п к общему числу частиц в расплаве N, т. е. p = n/N. Величина п, называемая скоростью воз­никновения центров кристаллизации (СВЦК), является важней­шей кристаллизационной характеристикой металлического рас­плава. Очевидно, n = p× N = p₁× p₂× N. Размерность [п] — м^-3× c^-1.

Для того чтобы определить вероятность p₁, рассмотрим вопрос о причинах появления зародышей в условиях возрастания сум­марной энергии Гиббса ΔG_å. С точки зрения статистической фи­зики характерные для равновесия значения термодинамических величин представляют собой лишь наиболее их вероятные при данных условиях значения. Практически отдельные микрообъемы жидкости в течение некоторых малых промежутков времени мо­гут обладать значениями термодинамических величин, отличными от отвечающих данному равновесному состоянию. При этом боль­шую часть времени система обладает равновесными термодинами­ческими характеристиками. Случайные отклонения какой-либо величины от ее равновесного значения называются флуктуациями. Вероятность обнаружения флуктуации зависит от ее величины. Чем больше флуктуация, т. е. отклонение от соответствующего равновесного значения, тем она менее вероятна и тем меньшее время система обладает соответствующим отличным от равновес­ного значением той или иной величины. Следует отметить, что кривая зависимости вероятности флуктуации от ее величины отли­чается острым максимумом в области нулевых флуктуаций (рис. 2.3). Поэтому с увеличением флуктуации вероятность ее появления резко снижается до нуля.

Благодаря наличию флуктуации энергии в расплаве будет находиться то или иное количество микрообъемов, обладающее избытком энергии, необходимым для совершения работы образо­вания зародыша критических размеров ΔG_кр. Вероятность такой энергетической флуктуации равна p_l = n_к/N = exp(—ΔG_кр/kТ), где n_к — число зародышей критического размера; N—общее число частиц в единице объема. Вероятность p₁ и будет вероятностью возникновения зародыша критического размера в единице объема в единицу времени. Очевидно, что, чем больше ΔG_кр, тем боль­шая требуется энергетическая флуктуация и меньше вероятность р₁. Так как с увеличением переохлаждения ΔT ΔG_кр уменьшается, то с ростом ΔТ повышается р₁. Вероятность присоединения к за­родышу хотя бы одной частицы равна p₂ = n_sen× exp(—U/kT), где n_s—число атомов в жидкости, находящихся в контакте с поверх­ностью зародыша; e = l/6 — вероятность скачка атомов в данном направлении; n — частота колебаний атомов в жидкости (n = 10¹³•c^-l); U—энергия активации диффузии атомов в жидкости, определяющая подвижность атомов.

Таким образом, вероятность образования центра кристаллиза­ции равна

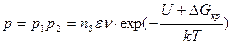. (2.1)

С учетом формулы (2.1) для вычисления скорости возникновения центров кристаллизации можно записать выражение

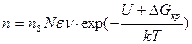. (2.2)

С увеличением переохлаждения ΔG_кр уменьшается, а U воз­растает (снижается подвижность атомов). Поэтому зависимость п от ΔТ носит экстремальный характер (рис. 2.4). Подобную кривую получил впервые в начале века Г. А. Тамман при кристал­лизации органических прозрачных жидкостей. Для чистых гомо­генных металлических расплавов зависимость п от ΔT показана на рис. 2.5. Видно, что при переохлаждениях, меньших величины ΔТ₁, называемой интервалом метастабильности по зарождению, зарождение центров кристаллизации практически не происходит. Для металлов ниспадающая ветвь кривой (см. рис. 2.4) не реа­лизуется, так как подвижность атомов в металлах очень велика.

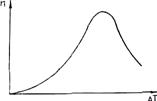
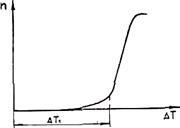
Рис. 2.4. Зависимость СВЦК " от переохлаждения ΔТ Рис. 2.5. Зависимость СВЦК от пере­охлаждения

для очистки гомогенных металлических расплавов

Для чистых гомогенных металлических расплавов величина интервала метастабильности очень велика. Расчеты показывают, что ΔT₁ » 0,2Т_кр. Реально подобная переохлаждаемость распла­вов не наблюдается, так как в расплаве всегда находится доста­точное количество примесей, инициирующих зародышеобразование.

Обычно самопроизвольную гомогенную кристаллизацию изу­чают на мельчайших каплях чистого металла. При этом считает­ся, что при измельчении металла вероятность нахождения при­меси в капле уменьшается. Зависимость n от ΔT для металлов можно аппроксимировать следующей степенной зависимостью: n = n₀(ΔT — ΔT₁)^s, где показатель степени s находится в интер­вале от 1 до 3.

Выше речь шла о самопроизвольном зарождении кристаллов при затвердевании однокомпонентных расплавов (чистых ме­таллов). Большинство литейных расплавов являются сплавами, т. е. высокотемпературными жидкими растворами. При этом про­дуктами кристаллизации чаще всего являются твердые растворы. При охлаждении до температуры ликвидуса жидкий сплав ока­зывается насыщенным по отношению к легирующему компоненту. Поэтому при дальнейшем снижении температуры наступает пересыщение и из расплава должны выделяться твердые кристаллы.

Свойства, не зависящие от количества вещества, называются интенсивными. К ним относятся температура и давление. При­менительно к растворам Г. Н. Льюис ввел еще одну интенсивную величину, называемую парциально-молярной величиной компо­нента. Она представляет собой частную производную от какого-либо экстенсивного свойства W по числу молей этого компонента при постоянных давлении, температуре и числе молей остальных компонентов в растворе, т. е. q_i = (дW/дn_i}_{p,T,n j¹i} Например, парциально-молярная энергия Гиббса для (i-го компонента равна G_i = (дG/дп_i)_{р,T, j¹i}. Легко понять, что парциально-молярные свойства чистых веществ совпадают со значением этих свойств одного моля

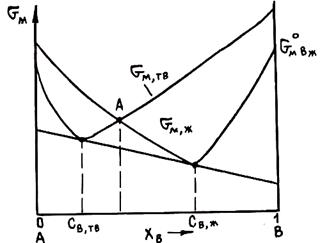
Рис. 2.6. Схема графического определения состава фаз, находящихся в равновесии при заданной температуре

вещества для заданных условий (G⁰A и G⁰B). Дейст­вительно, для вещества A G = nG⁰_A и дG/дп = G⁰_A. Величина дG/дп_i называется химическим потенциалом m_i, т. е. m_I = (дG/дп_i)_{P,T, j¹i} Химический потенциал характеризует тенден­цию вещества покинуть данную фазу и перейти в другую. Физи­чески химический потенциал равен работе, которую нужно со­вершить, присоединяя к раствору одну частицу данного компо­нента. Интенсивные величины Т, Р и m_I характеризуют условия термического, механического и химического равновесия. Для рав­новесия необходимо, чтобы во всех фазах были одинаковые тем­пературы, давления и химические потенциалы компонентов.

Приравняв величины m_I для каждого компонента во всех фа­зах, получим систему уравнений, которая совместно с уравнениями материального баланса позволяет найти составы находящихся в равновесии фаз. Для двойных сплавов этот подход хорошо реализуется графически. На рис. 2.6 показан пример графическо­го метода определения состава твердого раствора и находящейся с ним в равновесии при некоторой температуре Т жидкой фазы. При равновесии должны выполняться условия m^тв_А = m^ж_А и m^тв_В = m^ж_В, а если m_В = дG/дп_в, то составы фаз должны обеспечивать выполнение равенства

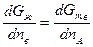или

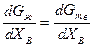
Геометрически это означает, что составы определяются общей касательной к кривым зависимости энергий Гиббса твердой и жидкой фаз при данной температуре. Эти равновесные составы G^тв_В и G^ж_В показаны на рис. 2.6. Иногда считают, что искомые составы отвечают точкам пересечения кривых мольных энергий фаз, например точке А, т. е. точкам, где равны энергии фаз. Од­нако равновесные фазы обеспечивают минимум суммарной энер­гии обеих фаз, а он достигается только при m^ж_А = m^тв_А и m^ж_В = m^тв_В.

Таким образом, при достижении пересыщения из раствора могут выделяться твердые растворы, концентрации которых от­личаются от исходной. При этом для начала процесса кристал­лизации необходимо пересыщение раствора, достигаемое его пере­охлаждением относительно температуры ликвидуса.

Движущая сила, создающая условия для выделения твердой фазы в сплавах, определяется так же, как и для металлов, по изменению энергии Гиббса системы.

При кристаллизации сплавов вместо справедливого для одно­компонентного металла выражения ΔG^м = L×ΔT'/T_пл следует при­менять выражение ΔG_ж-a С учетом этого для критического размера зародыша получим выражение r_кр = 2sМ/(r×ΔG^м_ж-а). Работа образования критического сферического зародыша равна 16pМ²s³/[Зr²(ΔG_ж-а)²].

Следует отметить, что зарождение центров кристаллизации сплавов, как показали исследования, качественно описывается той же зависимостью от переохлаждения, что и у металлов. При этом переохлаждение отсчитывается от температуры ликвидуса. Величину ΔG^м_ж-a можно также вычислить по формуле LΔT/Т_л, где L — теплота кристаллизации, выделившаяся при кристалли­зации единицы массы сплава при данной температуре.

Для образования зародышей твердых растворов необходимы не только рассмотренные выше энергетические флуктуации, но и флуктуации концентрации. Концентрационные флуктуации пред­ставляют собой участки растворов, состав которых отличается от среднего. Например, в жидком чугуне при средней концентрации углерода 3,4 % обнаруживаются участки размером 10^-8 см, состоящие из одного углерода. По-видимому, именно эти участки являются основой возникновения зародышей графита при кристал­лизации чугуна.

Рассмотренный выше процесс кристаллизации сплавов назы­вается диффузионным, так как при кристаллизации в этих слу­чаях происходит перераспределение компонентов между фазами путем диффузии.

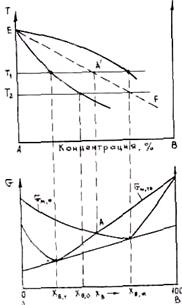
Рис. 2.7. Схема бездиффузион­ной кристаллизации

Возможен бездиффузионный про­цесс кристаллизации сплавов, когда состав выделяющейся твердой фазы строго совпадает с составом исход­ного жидкого сплава. На рис. 2.7 представлена диаграмма состояния и зависимость G от состава для жид­кого сплава и сплава в твердом со­стоянии. Зависимость G приведена при T = T₁. Точка A` отвечает равен­ству мольных энергий Гиббса твер­дой и жидкой фаз. На диаграмме состояния ей соответствует точка А`. Если аналогичные точки перенести на диаграмму при других температурах, то получим линию EF, отвечающую равенству G_т = G_ж. Если сплав рез­ко переохладить ниже этой линии (например до T = T₂), то G_т станет меньше G_ж и произойдет бездиффу­зионная кристаллизация с выделени­ем твердой фазы концентрации С₀. Анализ показывает, что для этого нужны очень большие пере­охлаждения (порядка нескольких десятков и даже сотен .граду­сов) В обычной литейной практике они не достигаются, так как требуют очень больших скоростей охлаждения при малых объ­емах сплава.

ГЛАВА 2.2. ТЕОРИЯ ГЕТЕРОГЕННОГО ЗАРОДЫШЕОБРАЗОВАНИЯ

Большинство металлов затвердевает при значительно меньшем переохлаждении, чем максимальное переохлаждение ΔT_mах = 0,2T_кр предсказываемое теорией гомогенного образования за­родышей. Это обусловлено наличием в расплаве инородных твер­дых частиц которые облегчают возникновение зародышей, Рас­смотрим простейший случай образования зародыша на плоской поверхности включения.

Пусть зародыш ограничен частью сферической поверхности радиуса R (рис. 2.8). Изменение полной мольной энергии сплава при образовании зародыша в данном случае имеет вид

,

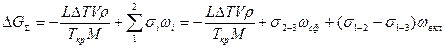где s_2-3 и s_1-2 — межфазные энергии на границах сплав — за­родыш и зародыш — включение; w_сф и w_вкл — площади поверхностей зародыша на границе со сплавом и на границе с включе­нием; s_1-3 — межфазная энергия на границе между включением и сплавом. Выполнив геометрические преобразования (предлага­ем читателю выполнить их самостоятельно), получаем следующие формулы для вычисления V, w_сф и w_вкл:

;

; .

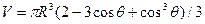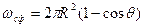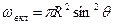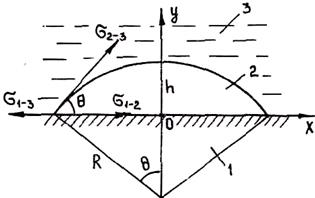
Рис. 2.8. Схема зарождения кристалла на плоской по­верхности включения:

/ — включение; 2 — зародыш; 3 — сплав

Подставив эти выражения в формулу для ΔG_å и выполнив исследования на максимум, получаем следующие выражения для вычисления энергии образования критического зародыша на вклю­чении и соответствующего ему размера R_кр:

;

.

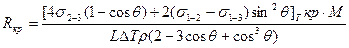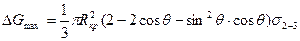Предлагаем читателю получить эти формулы самостоятельно.

При полном несмачивании включения сплавом (q = p) имеем сферический зародыш. При этом ΔG_mах = 4p(R*)²/3s_2-3. При полном смачивании (q = 0) ΔG_mах = 0. Сравним работу образова­ния зародыша на включении при 0 < q < 180° с работой гомоген­ного образования сферического зародыша:

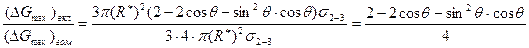<1 при 0 < q < p.

Таким образом, работа образования критического зародыша на включении меньше, чем в гомогенном расплаве. СВЦК при этом вычисляется по ранее приведенным формулам, если вместо ΔG_mах в них подставлять полученное выше выражение для расче­та максимального изменения энергии Гиббса при образовании зародыша на включении. Так как ΔG_mах при этом меньше, чем при гомогенном зарождении, то СВЦК при наличии включений увеличивается. Очевидно, что ΔG_mах становится меньше с умень­шением q, т. е. с усилением смачиваемости включения сплавом. Поэтому СВЦК увеличивается с уменьшением q.

Следует отметить, что не любые твердые включения резко увеличивают СВЦК. Из приведенных выражений видно, что это произойдет, если малы значения q и s_2-3. Очевидно, что s_2-3 бу­дет тем меньше, чем ближе кристаллическая структура включе­ния к кристаллической структуре зародыша. По правилу ориентационно-размерного соответствия, предложенного П. Д. Данковым и С. Т. Конобеевским, необходимо, чтобы включения имели один тип кристаллической решетки со сплавом. При этом параметры решеток не должны сильно отличаться. Такие включения назы­вают изоморфными. Указанное правило было обосновано П.Д. Дан­ковым следующим образом. На подкладке может образоваться ориентированный относительно ее решетки зародыш (он является как бы продолжением решетки включения) или произвольно ори­ентированный зародыш (как при гомогенной кристаллизации). Если параметры решеток различаются, то решетка зародыша, взаимодействуя с атомами решетки включения, упруго деформи­руется (расширяется или сжимается со сдвигом).

Если работа деформации меньше энергии образования трехмер­ного неориентированного зародыша, то зародышеобразования на включении не произойдет. Выполнив соответствующие расчеты для хлористого натрия, П. Д. Данков нашел, что ориентированное зарождение прекращается при различии в параметрах решеток соли и включения, равном 9 %. Практическая проверка формулы Данкова показала, что она дает завышение предельно допустимого отклонения параметров решеток. Практически при кристал­лизации соли хлористого натрия на галените ориентированное зарождение прекращалось при Δа/а = 5,7 %. В качестве примеров ориентированного зарождения центров кристаллизации металли­ческих расплавов можно привести рост медных кристаллов (а = 3,6Å) на никелевых включениях (а = 3,52Å), кристаллов a-латуни (а = 3,68Å) на серебре (а = 4,08Å). Измельчение кристаллического зерна в отливках вследствие увеличения СВЦК путем введения в расплав изоморфных

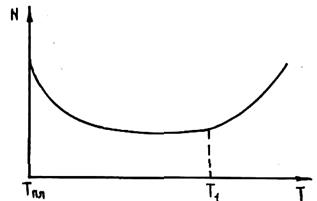
Рис. 2.9. Зависимость числа кристаллических зерен на единице площади шлифа от перегрева металла

примесей широко применяется на практике и называется модифицированием первого рода. Напри­мер, при введении в жидкий алюминий титана или циркония об­разуются тугоплавкие интерметаллические соединения TiAl₃ и ZrА1₃, имеющие изоморфную с алюминием кристаллическую решетку. Достаточно ввести в сплав десятые доли процента титана или циркония, как размер кристаллического зерна уменьшается в десятки и сотни раз.

Затравочное действие твердых включений зависит от термо­временной обработки расплава. На рис. 2.9 приведена зависи­мость числа кристаллических зерен N на единицу площади шли­фа от температуры обработки жидкого сплава. Видно, что с рос­том температуры перегрева сплава N уменьшается. Начиная с некоторой, хотя и очень высокой, температуры, ниспадающая кри­вая переходит в восходящую. Увеличение СВЦК при высоких пе­регревах объясняется тем, что при этом дезактивированы все включения и сплав кристаллизуется по гомогенному механизму в условиях очень больших переохлаждении.

Очевидно, что если в расплаве содержится большое число истинно изоморфных примесей, то их дезактивация при перегре­ве не происходит.

При увеличении перегрева сплава кроме отмеченных выше явлений может происходить растворение включений в расплаве или, наоборот, выделение их из расплава. В зависимости от ха­рактера выделяющихся или растворяющихся включений изменя­ется кристаллическая структура сплава. Например, при перегреве магниевых сплавов, легированных алюминием, марганцем и желе­зом, при некоторой температуре происходит растворение алюминиево-железистых соединений в расплаве. При охлаждении спла­ва в процессе кристаллизации эти соединения выделяются из рас­плава в виде компактных изоморфных частиц, что увеличивает СВЦК и измельчает структуру. Этот прием широко применяется в практике магниевого литья и носит название модифицирования перегревом. При перегреве чугуна происходит полное растворение углерода, что по аналогичным перегреву магниевых сплавов при­чинам приводит к резкому увеличению дисперсности выделяю­щихся при кристаллизации чугуна включений графита.

В заключение отметим, что при кристаллизации на примесях сохраняется характер изменения СВЦК с уменьшением переохлаж­дения. Однако при этом резко сокращается интервал метастабильности и повышается количественный уровень СВЦК. Это объясняется не только непосредственным влиянием переохлажде­ния на работу образования и размер критического зародыша, но и увеличением числа неизоморфных включений, удовлетворяющих сформулированному выше условию ориентированного роста.

Действительно, по данным Д. Тернбала и Б. Воннегута, энер­гия упругого деформирования кристалла на подкладке может

быть оценена по формуле ΔG = (а_вкл + a_м)²/a²_м, а движущая про­цесс разность энергий Гиббса при увеличении переохлаждения возрастает. Поэтому при увеличении переохлаждения все боль­шее число включений удовлетворяет условию ориентированного зарождения.

ГЛАВА 2.3. МЕХАНИЗМ И КИНЕТИКА РОСТА КРИСТАЛЛИЧЕСКИХ ЗАРОДЫШЕЙ

Образовавшиеся центры кристаллизации самопроизвольно уве­личивают свои размеры. Кристалл растет путем присоединения к нему атомов из окружающего расплава. Способ присоединения атомов к поверхности растущего зародыша определяется строением поверхности раздела фаз, распределением и количеством дефектов на этой поверхности. В соответствии с современной теорией кри­сталлизации механизм роста кристаллов определяется состоянием поверхности их граней. В зависимости от этого фактора можно выделить следующие механизмы роста кристаллов.

1. Рост кристаллов на атомно-гладких поверхностях кристал­ла. В этом случае все атомы поверхности раздела кристалл — расплав расположены на одной плоскости, на которой нет обра­зований адсорбированных атомов типа уступов, ступеней и т. п. Образование уступов, ступеней, выступов из групп атомов называется процессом огранки поверхности, которая при этом назы­вается ограненной.