Раздел 1. СТРОЕНИЕ И СВОЙСТВА ЖИДКИХ МЕТАЛЛОВ И СПЛАВОВ 3 страница

1.2.1. ПРОСТЕЙШИЕ РЕОЛОГИЧЕСКИЕ МОДЕЛИ ТЕЛ

Простейшим в реологическом отношении твердым телом явля­ется тело Гука (тело Н), для которого характерна линейная связь между напряжениями и относительными деформациями. Как из­вестно, на законе Гука основывается такая наука, как сопротив­ление материалов. В соответствии с этим законом при одноосном растяжении s = Еe, а при сдвиге t = gG, где s — нормальное (при­ложенное перпендикулярно площадке) напряжение; t — касатель­ное, т. е. действующее в параллельной плоскости, напряжение; e — относительная деформация растяжения (e = ∆l/l), т. е. отно­шение увеличения длины образца к его первоначальной длине; g — относительная деформация при сдвиге; Е — модуль упругости при растяжении (модуль Юнга) и G — модуль упругости при сдвиге.

Относительную деформацию при сдвиге можно определить в соответствии со схемой (рис. 1.16). Модуль упругости при сдвиге связан с модулем Юнга следующей зависимостью: G = E/[2(1 + m)], где m (коэффициент Пуассона) — отношение поперечной относительной деформации при сужении растягиваемого образца (поперечное сужение) к относительной деформации растяжения (для алюминия (m = 0,33, для стали m = 0,28, для бронзы m = 0,35). При растяжении s = F/S, где F — действующая сила; S — пло­щадь сечения образца, перпендикулярного направлению силы. Поэтому напряжения, создаваемые при растяжении,

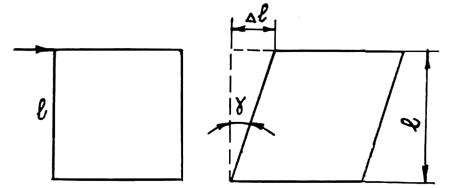
Рис. 1.16. Схема деформации при сдвиге

можно рас­сматривать как нормальные. При сдвиге t = f/s, где F—дейст­вующая сила, вектор которой лежит в плоскости S. Поэтому на­пряжение t называется касательным напряжением. В сложных случаях нагружения действующие силы создают одновременно и нормальные, и касательные напряжения.

В системе координат напряжение — деформация — время по­ведение тела Гука иллюстрируется схемой, приведенной на рис. 1.17. Суть состоит в том, что при приложении нагрузки в теле мгновенно возникают упругие деформации, пропорциональ­ные напряжениям. В процессе выдержки они не меняются. При снятии нагрузки размеры тела возвращаются в исходное положе­ние. В качестве механической аналогии тела Гука в реологии при­нята спиральная пружина, изображенная на рис. 1.18.

Естественно, что механическое поведение твердых тел не ис­черпывается моделью Гука, и с более сложными реологическими законами твердых тел мы познакомимся в дальнейшем. Сейчасжеперейдем к рассмотрению реологических законов жидкостей.

С точки зрения механического поведения жидкости отличаются от твердых тел текучестью и малой сжимаемостью. Текучесть — свойство тела развивать сколь угодно большие деформации под действием сколь угодно малых напряжений. В твердом теле под действием приложенных усилий развивается напряженное состояние которое характеризуется наличием касательной и нормаль­ной составляющей (рис. 1.19, а). Касательное напряжение t вызывает деформацию сдвига слоев тела вдоль плоскости тп. Напряжения носят упругий характер до тех пор, пока они непревзойдут некотором величины, называемой пределом текучести. При этом часть тела A начнет сме­щаться, т. е. течь относительно тела В по плоскости тп.

Жидкость в отличие от твер­дого тела в состоянии покоя не может развивать касательных напряжений, т.е. напряжения в ней (давления) всегда ориентированы перпендикулярно к площадке. В жидкости могут развиваться поэтому только нормальные на­пряжения. В силу этого касатель­ные составляющие приложенных к жидкости сил не могут быть уравновешены напряжениями и, какова бы ни была величина этих усилий, они приведут к неогра­ниченному смещению тела А относительно В, т. е. к течению (рис. 1.19, б). Можно сказать, жи­дкость — это среда, предел те­кучести которой равен нулю. Именно поэтому жидкость не име­ет своей формы, а принимает всегда форму сосуда. Если ее предоставить самой себе в усло­виях поля тяжести Земли, то она растечется до слоя, толщина которого имеет порядок размеров молекулы или атома. В отличие от газов жидкость не занимает всего предоставленного ей объема сосуда. Она имеет четко выра­женную поверхность раздела с воздухом.

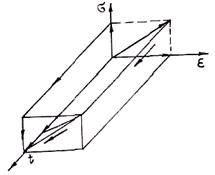
Рис. 1.17. Поведение тела Гука при нагружении и разгрузке

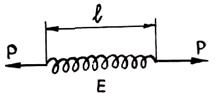
Рис. 1.18. Схема тела Гука (H-тела)

В движущейся жидкости между отдельными ее слоями, имею­щими разные скорости, возникают силы трения, препятствующие смещению слоев. Так как эти силы лежат в плоскости контакта слоев то они создают касательные напряжения. Рассмотрим по­ток жидкости в трубе. Скорости точек жидкости в любом ее по­перечном сечении распределены неравномерно. Ясно, что макси­мальное значение скорости имеет место на оси трубы, а на по­верхности контакта жидкости и трубы скорость равна нулю При­мер характера распределения скорости по сечению трубы (эпюра скорости) показан на рис. 1.20. Выделим в жидкости два слоя толщиной dr, поверхность контакта в которых АВ представляет собой цилиндр радиуса r. Вдоль поверхности АВ действует сила трения F₂, приложенная к слою 2, двигающемуся с большей ско­ростью, и сила F₁, приложенная к слою1, имеющему меньшую скорость. Видно, что сила трения стремится увеличить скорость медленно двигающегося слоя и уменьшить скорость быстро дви­гающегося слоя.

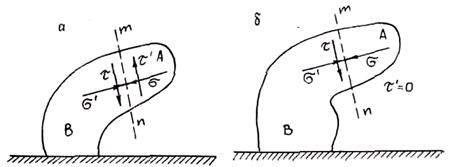
Рис. 1.19. Схема, поясняющая текучесть:

а — исходное положение; б — начало смещения (течения)

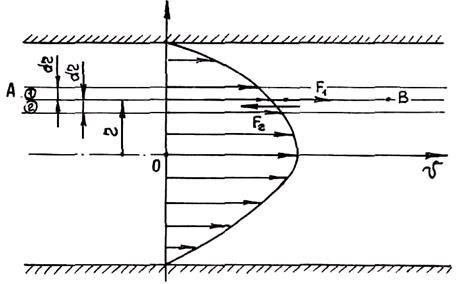
Рис. 1.20. Эпюра скоростей в потоке жидкости

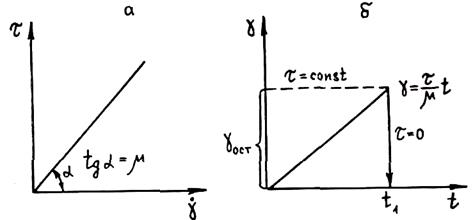
Рис. 1.21. График изменения напряжения (а) и поведения тела Ньютона (б) при постоянной нагрузке (t - const)

Закон трения в жидкостях впервые был сформулирован Ньюто­ном: F = hSdv/dr, где h —динамический коэффициент вязкости жидкости; S — площадь контакта слоев; dv/dr — градиент скоро­сти. Разделим обе части формулы Ньютона на площадь контакта слоев S. В результате получаем t = mdv/dr, где t — касательное напряжение. Величину dv/dr преобразуем, приняв, что v = dl/dt; dv/dr = d(dl/dr)/dt, где dl/dr = g — относительная деформация при сдвиге, a dg/dt = g — скорость деформации. Значит, t = mg. Это реологический закон ньютоновской жидкости, или тела Нью­тона. Суть его в том, что касательные напряжения в движущейся ньютоновской жидкости пропорциональны скорости деформации, а не самой деформации, как у тела Гука. Графически этот закон изображен на рис. 1.21. Из рисунка видно, что, как бы ни были малы напряжения, наступает вязкое течение материала. При этом абсолютная деформация непрерывно растет во времени. При сня­тии напряжения течение прекращается, но накопленная деформа­ция сохраняется. Таким образом, вязкое течение приводит к не­обратимым остаточным деформациям. Вязкость жидкости является ее важнейшим физико-химическим свойством. Графически тело Ньютона (N-тело) изображается, как показано на рис. 1.22.

Поведение жидкостей не исчерпывается реологическим зако­ном тела Ньютона. Имеется класс жидкостей, описываемых дру­гими законами и называемых неньютоновскими жидкостями. Про­стейшей неньютоновской жидкостью является тело Бингама, или Бингамов пластик, а также тело Сен-Венана. Тело Сен-Венана (S-тело) называется пластическим телом. Реологическое уравне­ние S-тела имеет вид s = s_s для растяжения и t = t_s для сдвига. Здесь s_s — предел текучести при растяжении и t_s — предел теку­чести при сдвиге. При напряжении, меньшем предела текучести, тело Сен-Венана является абсолютно твердым упругим телом. При s = s_s (или t = t_s) материал пластически течет со скоростью, равной скорости деформирования (при штамповке; например, со скоростью движения пуансона). При этом, несмотря на увеличе­ние нагрузки, напряжение не возрастает. В качестве механической аналогии тела Сен-Венана в реологии принят элемент сухого тре­ния. Графически поведение S-тела показано на рис. 1.23. Тангенс угла a на рисунке равен скорости деформирования.

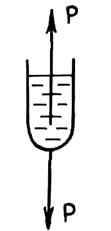
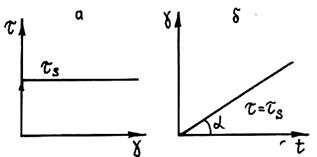
Рис. 1.22. Схема тела Ньютона N-тела) Рис. 1.23. Зависимость t (g) (а) и поведение тела Сен-

Венана при t = t_s (б)

Тело Бингама (B-тело) представляет собой параллельно со­единенные тела Ньютона и Сен-Венана, последовательно вклю­ченные с телом Гука (H-телом). B-тело называется вязкопластичной жидкостью (рис. 1.24). При последовательном соединении элементов их напряжения одинаковы и равны приложенным на­пряжениям, т. е. t = t = t_sn, где t_н — напряжение элемента Гука, a t_SN—напряжения параллельной комбинации тел Ньютона и Сен-Венана. Деформации элементов при этом могут быть различ­ными. Общая деформация равна сумме деформаций отдельных последовательно соединенных элементов. Таким образом, g = g_H + g_SN (рис. 1.25).

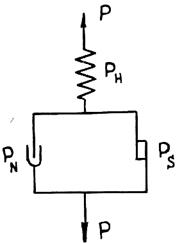
Рис. 1.24. Схема тела Бингама (В-тела)

При параллельном соединении деформации обоих элементов одинаковы, а сумма их напряжений равна приложенному к системе напря­жению. Для указанной схемы g_SN = g_n =g_s и t = t_H = t_N + t_S. При t < t_S g_SN = 0 и g = g_H + g_SN = g_H. При t ³ t_S g = g_sn + g_h = t_N/h_N; t_N = t - t_S и g = (t —t_S)/h_N. Отсюда получаем, что t = t_S + h_Ng. Это реологический закон В-тела. Величина t_s называется пре­дельным касательным напряжением сдвига, а h_N - структурной динамиче­ской вязкостью тела. К телам Бингама можно отнести переохлажденные нефти, масла, битумы, суспензии и пе­реохлажденные сплавы при температу­рах, относительно близких к темпера­туре ликвидуса.

Описание реологического поведе­ния реальных тел не исчерпывается описанными моделями. Более сложные модели будут рассмотрены в соответствующих разделах курса.

1.2.2. ВЯЗКОСТЬ ПЕРЕГРЕТЫХ ЖИДКИХ СПЛАВОВ

Исследования по течению расплавленных металлов и сплавов при температуре выше температуры ликвидуса показали, что жид­кие сплавы по своему поведению близки к вязким ньютоновским жидкостям. Важнейшей характеристикой жидких металлов и сплавов является их вязкость. Выше было сказано, что вязкость есть свойство жидкостей оказывать сопротивление взаимному смещению слоев. Разрешив реологический закон ньютоновских жидкостей относительно динамического коэффициента вязкости h, найдем его размерность в СИ: [h] =Н×с×м/(м²м) = Н×с/м². В системе CGS [h] = дин×с/см²; она называется пуаз. Легко получить соотношение между единицами: lH×c/м² = 10 пуаз = 1000 сантипуаз, где сантипуаз — сотая доля пуаза.

В гидродинамике большое значение имеет кинематический коэффициент вязкости v = h/r. Его размерность в СИ — м²/с, в CGS — см²/с. Видно, что 1 м²/c = 10⁴ стокс. Стокс —название раз­мерности v в системе CGS. Сотая доля стокса называется сантистокс.

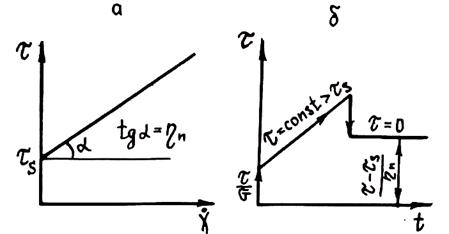
Рис. 1.25. Зависимость t(g) (а) и поведение .В-тела при t >t_s (б)

Динамический коэффициент вязкости жидких металлов и сплавов имеет порядок от 1,8 • 10^-3 Н^.с/м² (у олова) до 7,4 • 10^-3 Н^.с/м² (у чугуна). Кинематический коэффициент вязко­сти охватывает значения от 0,26 • 10^-6 м²с (у олова) до (1,2—1,6) • 10^-6 м²с (у алюминия). Для сравнения приведем дан­ные по вязкости воды при комнатной температуре: h = 1,05 • 10^-3 Н^.с/м² и n = 1,05 • 10^-6 м²с. Видно, что вязкость v у металличе­ских расплавов близка к кинематической вязкости воды.

Вязкость характеризует текучесть жидкости, которая равна 1/h. Приведенные данные показывают, что жидкие металлы об­ладают хорошей текучестью. По Я. И. Френкелю, который рас­сматривает жидкость как среду с повышенной концентрацией вакансий (дырок), в жидкости колебательное движение атомов относительно некоторых положений равновесия сочетается с тран­сляционным поступательным движением атомов (трансляция ды­рок и дислоцированных атомов). Очевидно, что, чем меньше время оседлой жизни атома, тем больше текучесть и меньше вяз­кость.

В связи с этим для вычисления динамического коэффициента вязкости Я. И. Френкель предложил следующую формулу: h = A • e^E/RT, где Е — энергия активации вязкого течения (для чи­стых металлов Е = 7—50 кДж/г ^. атом; А — предэкспоненциальный множитель, зависящий от межчастичных расстояний в жидкости, частоты колебаний атомов и т. п. Из формулы видно, что вязкость с повышением температуры уменьшается (в отличие от газов). Экспериментальные данные показывают, что в определенном тем­пературном интервале зависимость h от температуры удовлетво­рительно описывается формулой Я. И. Френкеля. Однако в предкристаллизационный период и при значительных перегревах на­блюдаются существенные отклонения. На рис. 1.26 приведен характер изменения вязкости Аl в предкристаллизационной области. Видно, что при температурах, близких к Т_кр, вязкость резко уве­личивается. Аналогичная картина имеет место и у сплавов.

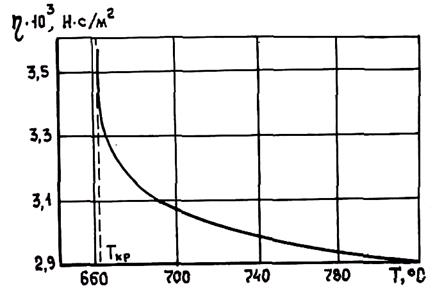
Рис. 1.26. Зависимость динамического коэффициента вязкости h| жидкого алюминия от температуры

С позиций современной кластерной теории жидкого состояния характер изменения вязкости с повышением температуры можно объяснить следующим образом. После расплавления жидкость имеет микронеоднородное строение, характеризующееся наличи­ем кластеров, взаимодействующих с областями межкластерных разрывов. При этом в сплавах существуют кластеры разного типа и разной устойчивости. Лавинный рост вязкости вблизи темпера­туры кристаллизации (для алюминия начиная с температуры 670°С) можно объяснить большой концентрацией кластеров, при которой они образуют непрерывную сетку (каркас), и малым объемом межкластерных разрывов (1—6%), что приводит к низ­кой подвижности кластеров. Жидкость имеет при этом структуру в виде квазикаркаса поликластеров.

С повышением температуры устойчивые кластеры дробятся на монокластеры, размеры которых на порядок меньше, что при­водит к резкому падению вязкости. Силы связи между кластера­ми уменьшаются, и вязкость плавно убывает по экспоненте. При некоторой температуре, которую называют температурой разупорядочения, кластеры разрушаются. Жидкость имеет структуру однородной среды статистически распределенных атомов, между которыми велики еще силы взаимодействия. Вязкость при этом убывает с ростом температуры близко к линейному закону. Та­ким образом, вязкость является структурно чувствительным свой­ством, и по характеру ее температурного изменения можно судить о структурных превращениях в жидких расплавах.

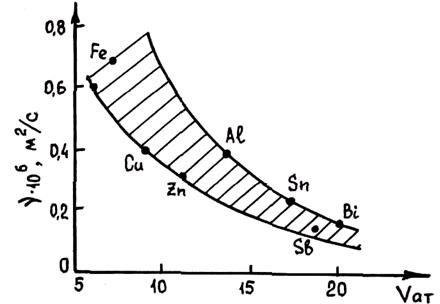
Рис. 1.27. Зависимость кинематической вязкости v жидких металлов от их атомарного объема

Исследованиями обнаружена четкая корреляция вязкости с объемом, приходящимся на один атом жидкого металла V_ат. Ки­нематическая вязкость n большинства металлов при температу­рах, близких к температуре затвердевания, удовлетворительно описывается функцией n = К/Vат, где К—коэффициент, прибли­зительно равный 4—5. Соотношение между n и V_ат показано на рис. 1.27 для целого ряда жидких металлов. Связь вязкости с величиной свободного объема металла, не занятого атомами, вы­ражает эмпирическая формула А. И. Бачинского n = =с/(Vат - w), где с и w — эмпирические коэффициенты, не зависящие от дав­ления и температуры. Величина w имеет смысл собственного объ­ема атомов, так что разность (Vат - w) характеризует величину свободного объема.

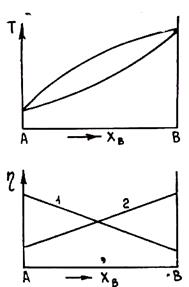
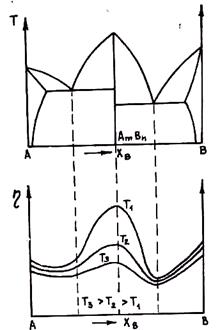
Рис. 1.28. Зависимость вязкости сплавов Рис. 1. 29. Зависимость вязкости сплавов с

с неограниченной рас­творимостью интерметаллидами от состава

компонентов в твердом состоянии от

состава и температуры перегрева

Смысл указанных формул сводится к тому, что с увеличением расстояния между атомами или кластерами увеличивается их подвижность и уменьшается вязкость. Подобная связь со свобод­ным объемом позволяет интерпретировать влияние давления на вязкость. Увеличение давления приводит к уменьшению свобод­ного объема и увеличению вязкости. Эту зависимость можно описать формулой h = h₁ • e^{b P}, где h₁ — вязкость при атмосферном давлении (Р = 0,1 МПа); h — вязкость при давлении Р; b — ко­эффициент, равный 1/30—1/50. Эта формула удовлетворительно описывает изменение вязкости неметаллических жидкостей. У ме­таллов коэффициент значительно меньше. Поэтому темп нараста­ния вязкости с увеличением давления мал. Например, при увеличении давления с одной атмосферы до 1200 атмосфер (120 МПа) вязкость возрастает для жидкой ртути всего в пол­тора раза.

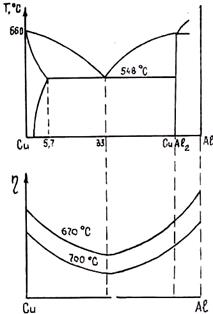
Рис. 1.30. Зависимость вязкости спла­вов с эвтектическим превращением от состава и температуры перегрева

При легировании металлов, т. е. при образовании сплавов, вязкость изменяется по сложным законам. Если сплавляемые компоненты образуют идеальный раствор (силы взаимодействия компонентов A и В в бинарном растворе F_AA » F_BB » F_AB), то вязкость раствора линейно связана с его концентрацией, выра­женной в мольных долях, в соот­ветствии с формулой h = X_Ah_A + X_Bh_B, где h_A и h_B — вязкости чистых компонентов при данной температуре, Х_A и Х_B — мольные доли компонентов. Этому случаю соответствует диаграмма с непре­рывным рядом твердых раство­ров. На рис. 1.28 изображен ха­рактер зависимости г) таких спла­вов от концентрации, выражен­ной в атомных процентах. Кри­вая 1 отвечает случаю, когда h_A > h_B, а кривая.2 — h_A < h_B. Реально зависимость может откло­няться от линейной, но ее харак­тер сохраняется. Такое поведе­ние вязкости сплавов отвечает описанной выше структуре жи­дких сплавов подобного типа.

У сплавов с образованием ин­терметаллических соединений на кривой зависимости вязкости от концентрации наблюдается мак­симум, отвечающий составу интерметаллида. Этим сплавам соответствуют следующие соотношения сил взаимодействия: F_AB > F_AA; F_AB > F_BB, что, как было показано выше, приводит к уси­лению микрогетерогенности расплава, особенно возрастающей при концентрации, отвечающей составу интерметаллида (класте­ры имеют структуру и состав, отличающиеся от соответствующих характеристик жидких компонентов). Характер такой зависимо­сти приведен на рис. 1.29. Как видно из рисунка, по мере повы­шения температуры максимумы сглаживаются, так как происхо­дит ослабление связей и распад соединений. Следует отметить, что если кривые относить к одинаковым перегревам над ликви­дусом, то значительные максимумы не наблюдаются (в примере, изображенном на рисунке, соединение наиболее тугоплавкое, и при одинаковой для всех составов температуре ему будет отве­чать наименьший перегрев над ликвидусом). Подобный характер изменения вязкости имеет место, если интерметаллид образуется непосредственно из жидкого состояния, а не при затвердевании. В последнем случае максимум не наблюдается (например в спла­вах серебра с оловом).

Рассмотрим в заключение характер зависимости вязкости сплавов с эвтектическим превращением от их состава. В этих си­стемах наименьшей вязкостью обладают сплавы эвтектического состава. Это можно объяснить тем, что в таких сплавах F_AB > F_A; F_AB > F_B, т. е. имеет место слабое взаимодействие между разно­родными атомами. Кроме того, при заданной температуре эвтек­тические сплавы имеют наибольший перегрев над ликвидусом.

Следует отметить, что в вопросе зависимости вязкости спла­вов от концентрации еще имеется много противоречий, особенно для сплавов с ограниченной растворимостью в твердом состоя­нии. На рис. 1.30 приведены кривые изменения вязкости в сплаве системы алюминий — медь.

1.2.3. РЕОЛОГИЧЕСКИЕ СВОЙСТВА СПЛАВА В ИНТЕРВАЛЕ КРИСТАЛЛИЗАЦИИ

При охлаждении сплава ниже температуры ликвидуса из жид­кого раствора начинают выпадать кристаллы твердого раствора. При этом в равновесных условиях количество выделившейся твер­дой фазы при любом значении температуры внутри интервала кри­сталлизации можно определить по правилу рычага. По мере уменьшения температуры относительная массовая доля твердых включений в расплаве непрерывно увеличивается. Таким образом, расплав при температуре, меньшей температуры ликвидуса, пред­ставляет собой суспензию, концентрация которой при охлаждении увеличивается. Если в суспензии расстояния между твердыми ча­стицами значительно превышают размеры частиц, то такая сус­пензия в реологическом плане представляет собой ньютоновскую жидкость, обладающую некоторой эффективной вязкостью.

Впервые формула для расчета вязкости суспензий была полу­чена А. Эйнштейном для сферических твердых включений. Фор­мула имеет вид h = h₀(1 + 2,5ℋ), где h₀ — динамический коэффи­циент вязкости диспергированной среды; ℋ = 4pr³n/3 — отношение суммарного объема всех включений к полному объему суспензии; r — радиус включения; п —число включений в единице объема суспензии. Для кристаллитов произвольной формы формула име­ет вид h = h₀(1 + kℋ), где k — относительный объем суспендированного вещества; ℋ — коэффициент, зависящий от формы вклю­чений. Для сферических включений k = 2,5; для эллипсоидных включений ℋ = 4ab²np/3 . По мере увеличения отклонений от а/b = 1 коэффициент k увеличивается. Например, при a/b = 1 k = 2,5, при а/b = 0,1 k = 8,04 и при а/b = = 10 k=13,6. Таким образом, на­личие в жидкости суспендированных включений приводит к уве­личению ее вязкости. При этом на вязкость оказывает влияние не только относительный суммарный объем включений, но и их форма. При этом вязкость тем больше, чем сильнее отклонение формы включений от сферической.

Следует подчеркнуть, что формула А. Эйнштейна справедли­ва при относительном объеме твердой фазы, не превышающем некоторой предельной величины ℋ_пр. Величина ℋ_пр зависит от фор­мы включений. Чем больше отклонение от сферической формы, тем меньше ℋ_пр. Например, для включений инфузорной земли в воде ℋ_пр = 15%, а для включений графита, вследствие их мень­шей округленности, ℋ_пр = 5%. Применимость формулы А. Эйн­штейна ограничивают ℋ_пр = 8%.

Влияние твердых включений на вязкость необходимо учиты­вать не только в сплавах ниже температуры ликвидуса, но и в перегретых сплавах, всегда содержащих то или иное количество неметаллических включений. Это могут быть продукты раскисления стали (Si0₂, MnO, Al₂O₃), графитовые включения в чугуне, продукты окисления алюминия Аl₂О₃, магния MgO, титана ТiO₂ и т. п. Кроме того, включения в расплав могут попадать за счет разрушения формы, огнеупоров и т. п. Например, при плавке чугуна с использованием в шихте высококремнистых литейных чугунов в нем содержится много включений графитовой спели. При этом сильно возрастает вязкость, что приводит к резкому снижению заполняемости форм чугуном даже при его высоком перегреве.

При снижении температуры сплава в интервале кристаллиза­ции ниже некоторой критической температуры Т₁, отвечающей критическому содержанию твердой фазы ℋ_пр, формула А. Эйн­штейна становится несправедливой, так как расплав изменяет свою реологическую природу. При концентрации суспензии ℋ_пр при достаточно близком расстоянии между частицами устанав­ливаются значительные силы взаимодействия. В результате об­разуется связная структура, которая способна сопротивляться сдвиговым усилиям, если развиваемые ими касательные напряже­ния не превосходят некоторого предельного напряжения сдвига t_s. При этом реологическое поведение сплава можно с некоторым приближением описать моделью тела Бингама (t = t_s + m_ndv/dr).

При снижении температуры ниже некоторой температуры T₂ < T₁ < T_л между частицами остаются тонкие прослойки жидкости. Отдельные частицы приходят в контакт друг с другом, упругие свойства образовавшейся структуры и предельное для нее напряжение сдвига t_s возрастают более резко. В этих условиях сплав находится в состоянии пасты.

При охлаждении сплава ниже критической температуры Т₃ < T₂ < T₁ < T_л частицы стыкуются друг с другом, образуя пори­стую среду. Упругие характеристики среды и предельное напря­жение сдвига резко возрастают. Жидкость при этом находится в межзеренных порах. Сначала они открыты и сообщаются друг с другом, так что возможны фильтрационные

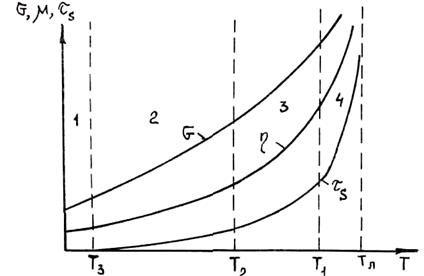
Рис. 1.31. Зависимость реологических характеристик от температуры в интервале кристаллизации

перемещения жидко­сти по объему тела. При температурах, близких к температуре солидуса, поры разобщаются и содержащиеся в них объемы жид­кого сплава оказываются изолированными, исключая возмож­ность фильтрации. При температуре солидуса жидкость в порах затвердевает.

Указанные зоны состояния сплава в интервале кристаллиза­ции и характер изменения вязкости, предельного напряжения сдвига t_S и модуля упругости с повышением температуры пока­заны на рис. 1.31. В первой зоне сплав ведет себя как ньютонов­ская жидкость, проявляя способность к вязкому течению при лю­бых как угодно малых касательных напряжениях. Во второй тем­пературной зоне сплав ведет себя как тело Бингама. При напря­жениях, меньших предельного напряжения сдвига t_s, среда не имеет пластической деформации и ведет себя как тело Гука. При t > t_S сплав течет как ньютоновская жидкость, эффективная вяз­кость которой увеличивается с понижением температуры. В тре­тьей зоне сплав сохраняет способность к пластическому течению при t > t_S, но характер его реологического поведения сложнее, чем у тела Бингама. В четвертой зоне структура ведет себя как гуковское тело вплоть до ее разрушения при достаточно больших напряжениях. При приложении давления расплав перемещается фильтрацией по межзеренным порам.

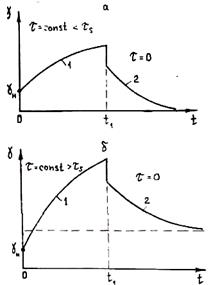
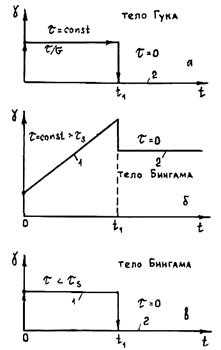
Рис. 1.32. Поведение сплава в интер­вале Рис. 1.33. Поведение сплава в соот­ветствии

кристаллизации при t < t_S (а) и при t > t_S (б) с составляющими его моде­лями Гука (а) и Бингама

при t > t_S (б) и t < t_S (a)

Для того чтобы установить реологическую модель сплавов в интервале кристаллизации, были проведены эксперименты по изучению зависимости величины деформации от времени при раз­ных значениях напряжений и разных температурах. Характер полученных кривых развития деформации во времени при посто­янном напряжении и заданной температуре показан на рис. 1.32. В течение времени 0 — t₁ на сплав действует нагрузка. В момент времени t = t₁ нагрузка мгновенно снята, и при t > t₁ кривая 2показывает поведение деформации при разгрузке образца. Ана­лизируя характер кривых, можно сделать вывод, что мы имеем дело со сложным реологическим телом. Оно содержит упругое тело Гука, так как на рисунке мы видим мгновенную деформа­цию при t = 0, которая сразу же снимается при t = t₁.