Раздел 1. СТРОЕНИЕ И СВОЙСТВА ЖИДКИХ МЕТАЛЛОВ И СПЛАВОВ 2 страница

Разрешение этого противоре­чия осуществляется путем потери дальнего порядка. Новые вакан­сии могут образовываться только лишь в пустотах плотной упаков­ки СД (рис. 1.10, б). Скопления и перемещения вакансий по гра­ницам СД приводят к тому, что решетка дробится на отдельные блоки, равные по размерам диаметру СД. Эти блоки называются кластерами. Таким образом, в пределах кластера сохраняется по­рядок в расположении атомов (ближний порядок), но за преде­лами кластера порядок нарушается (нет дальнего порядка).

Для дробления решетки на кластеры необходимо затратить энергию на разрыв связей кластеров друг с другом. Эта энергия и представляет собой теплоту плавления. Температура Гц, при которой смыкаются СД, равна температуре плавления. При плав­лении происходит изменение объема, вызванное двумя следующи­ми эффектами. Вследствие отталкивания друг от друга образо­вавшихся кластеров происходит увеличение объема. С другой стороны, так как при плавлении силы связи между кластерами резко уменьшаются, увеличивается их подвижность. До перехода в жидкое состояние зоны СД связаны между собой и сохраняют упаковку, характерную для кристалла. После плавления связи между кластерами разрушаются, они получают возможность сме­щаться относительно друг друга.

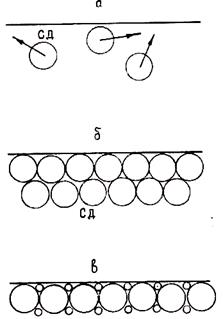
Рис. 1.10. Схема плавления по И. В. Гаврилину и Г. С. Ершову: а – Т<<T_пл; б – T » Т_пл; в – Т = Т_пл

Известно, что минимуму энергии отвечает более плотная упа­ковка (минимальная поверхность). Поэтому в жидкости кластеры принимают более плотную упаковку, чем та, которая была в кри­сталле. Благодаря этому эффекту объем жидкости должен быть меньше объема кристалла. Результирующее изменение объема при плавлении равно алгебраической сумме этих эффектов. Для большинства металлов превалирует первый эффект и объем при плавлении увеличивается примерно на 3%. Для таких аномаль­ных веществ, как висмут, галлий, сурьма, кремний, превалирует эффект переупаковки кластеров и объем при плавлении уменьша­ется. Кластеры в жидкости находятся в сложном тепловом дви­жении. При этом происходят процессы их воссоединения (вос­становления связей) и последующего дробления, но уже по дру­гим поверхностям разрыва.

Следует отметить, что теплота плавления значительно меньше теплоты испарения, а изменения объема невелики. Поэтому силы связи между частицами в жидкости остаются практически на том же уровне, что и в кристалле. Однако возрастает энергия тепло­вого движения. Это позволяет считать, что при температурах, близких к температуре плавления, жидкости ближе к кристал­лам, чем к газам.

В заключение необходимо отметить, что теория плавления в настоящее время еще не создана. Приведенная теория может рассматриваться как некоторое приближение.

1.1.3. МОДЕЛИ ЖИДКОГО СОСТОЯНИЯ

До сих пор не созданы такие эффективные модели жидкого состояния, какими являются модель идеального газа для газов и идеального кристалла для кристаллических тел. Все существую­щие модели жидкого состояния можно разделить на две большие группы: квазигазовые модели и квазикристаллические модели.

Общим для псевдогазовых моделей является игнорирование межчастичного притяжения. Взаимодействие частиц сводится только к их упругим столкновениям. Простейшей является мо­дель «твердых шаров». Частицы жидкости уподобляются твер­дым взаимно непроникающим шарам. Потенциал их взаимодей­ствия задается в следующем виде:

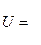^ f0, если г > 2R^, ~ [со, если г < 27?щ.

Смысл формул сводится к тому, что частицы не взаимодейст­вуют друг с другом, пока не столкнутся. При столкновении воз­никают упругие силы отталкивания. Радиус шаров принимают или равным радиусу первой координационной сферы кристалла, или на основании рентгенографического исследования жидкости (рас­стояние до первого максимума интенсивности рассеивания излу­чения). Так как под действием сил отталкивания при отсутствии притяжения частицы разлетятся, то вводится некоторый коэф­фициент их упаковки h = pd³N₀/6V₀, где Vo—мольный объем жид­кости; No—число Авогадро. Коэффициент упаковки выбирают для конкретной жидкости.

На основании выбранных значений h и d, а также принятого для твердых сфер указанного выше потенциала можно матема­тически определить радиальную функцию распределения частиц, т. е. число частиц, окружающих данную частицу, как функцию расстояния от нее. При этом расчетные значения функции рас­пределения неплохо согласуются с экспериментальными данными для некоторых металлов с плотными структурами кристаллов, т.е. для гексагональной решетки и гранецентрированного куба. Вме­сте с тем для большинства металлов расчетные и эксперименталь­ные данные расходятся.

С целью улучшения этой модели в 60-е гг. Дж. Бернал вместо твердых шаров предложил другие конфигурации частиц. Он про­вел эксперименты с пластилиновыми шарами, подвергнув конст­рукцию из этих шаров всестороннему сжатию. После сжатия ча­стицы принимали форму многогранников с гранями от треуголь­ных до 12-угольных. Однако значительная часть (больше 30%) частиц принимали вид многогранника с пятиугольными гранями. На основании этого Дж. Бернал сделал вывод, что в жидкости вокруг атома может образовываться кольцо из 5 «соседей». В кри­сталлах такого координационного числа нет. В остальном модель Бернала остается моделью твердых сфер, отличие состоит в том, что взаимодействуют не отдельные шары, а некоторые их кон­фигурации, имеющие вид рассмотренных выше фигур, в вершинах которых расположены частицы. Теория Бернала дает неплохие результаты для ряда сжиженных газов (аргон, гелий и т. д.).

Общим недостатком псевдогазовых моделей является игнори­рование фактических данных о наличии в жидкости достаточно сильных сил связи. Практически эти модели никак не объясня­ют, почему жидкость сохраняет свой объем и ее частицы не раз­летаются, занимая весь предоставленный объем, как в газах. Чем вызывается плотность упаковки?

Общим для всех квазикристаллических моделей является по­пытка при описании жидкого состояния учесть специфику сил межчастичного взаимодействия, установить связь структуры жидкости с предшествующим плавлению кристаллическим строением вещества.

Согласно сиботаксической модели Стюарта жидкость состоит из множества хаотически ориентированных микрокристаллических областей — сиботаксисов. Эту модель можно считать частным слу­чаем квазиполикристаллических моделей. В современном виде идеи этих моделей сформулированы В. И. Архаровым и И. А. Новохатским. Жидкость состоит из двух структурных составляю­щих: кластеров и разупорядоченной зоны. В разупорядоченной зоне структура и тепловое движение соответствуют сильно сжа­тым реальным газам. В кластерах структура и тепловое движение соответствуют кристаллам. Между кластерами и разупорядочен­ной зоной нет четко выраженной границы раздела. Эта точка зре­ния в том или ином виде развивается в других квазикристалли­ческих моделях. Отличия состоят в толковании кластера, харак­тера его движения и межкластерного взаимодействия. Выше мы описали подход к понятию кластера как коллектива частиц кри­сталла, находящегося внутри сферы деформации около вакансии. Следует заметить, что внутри кластера исходная структура кри­сталла не повторяется, сохраняется только ближний порядок, т. е. конфигурации первых координационных сфер решетки кристалла.

Все квазикристаллические модели трудно поддаются количест­венному математическому описанию.

1.1.4. МАТЕМАТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЖИДКОГО СОСТОЯНИЯ

Выделим в среде частицу и проведем сферический слой тол­щиной dR на расстоянии R от этой частицы. Пусть в этом слое находится dN частиц. Число частиц в единице объема вещества на расстоянии R выразится формулой r(R) = dN/(4pR²dR). Эта величина в общем случае зависит от расстояния R. Она называ­ется радиальной функцией распределения частиц и полностью ха­рактеризует структуру вещества. Для идеальных газов характер­но хаотическое распределение молекул. Поэтому в среднем в каждой точке газа содержится одинаковое число молекул. В этом случае r(R) не зависит от координаты R и совпадает с объемной плотностью частиц. В идеальных кристаллах частицы располо­жены только на координационных сферах. Поэтому r(R) между сферами равна нулю. Графически функция радиального распре­деления частиц в гранецентрированной решетке показана на рис. 1.11 (R—атомный радиус).

Жидкость—динамическая система. Поэтому распределение частиц в ней носит случайный характер. Для описания r(R) сле­дует поэтому использовать аппарат теории вероятностей.

Вероятность того, что в сферическом слое около молекулы 1 можно обнаружить частицу 2, равна dP(R) = W(R)• 4pR²dR/N. Смысл этого выражения сводится к следующему. Представим, что на бумаге начерчен круг радиуса R₁, внутри которого нахо­дится круг меньшего радиуса R₂. Мы с закрытыми глазами ста­вим внутри большого круга точку. Как оценить вероятность того,

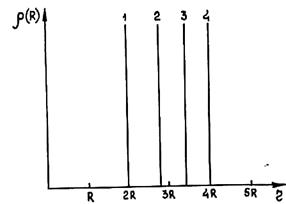
Рис. 1.11. Радиальная функция распределения для гранецентрированного кубического кристалла

что точка попадет внутрь малого круга? Если R₂ = R₁, то оче­видно, что вероятность равна 1. Будем уменьшать радиус малого круга. Ясно, что вероятность будет уменьшаться. Если R₂ = 0, то вероятность равна нулю. Поэтому вероятность (отношение числа положительных исходов к общему числу испытаний) можно вы­числить как отношение площади малого круга к площади боль­шого круга. Это будет справедливо, если положение частицы 2 не зависит от положения частицы 1.

Если между частицами есть силы взаимодействия, то очевид­но, что вероятность нахождения частицы 2 на расстоянии R за­висит от того, находится или нет частица / в начале координат. Этот факт учитывается множителем W(R), который называется корреляционной функцией распределения. Если частицы не вза­имодействуют, ясно, что W{R} = 1. В случае взаимодействующих частиц W{R) ¹ 1. Так как вероятность нахождения частицы в бес­конечной области около данной частицы равна 1, то для корре­ляционной функции можно написать следующее нормировочное соотношение: 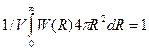. Выразим число частиц в сферическом слое толщиной dR через радиальную функцию рас­пределения: dN = r(R)4pR²dR. Проинтегрировав это выражение по всему объему среды, получим соотношение 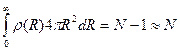. Сравнивая его с нормировочным соотношением на­ходим, что W(R)=V/N×r(R)=r(R)/r₀, где r₀ = N/V — среднее число частиц в единице объема. Значит, функция W(R) пред­ставляет собой относительную вероятность нахождения ча­стиц на заданном расстоянии R от фиксированной молекулы. Из последней формулы нахо­дим p(R) = r₀W(R), т. е. для определения радиальной функ­ции распределения нужно знать корреляционную функ­цию.

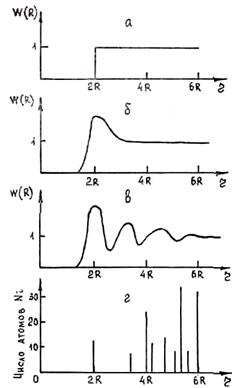
Рис. 1.12. Зависимость корреляционной функции от расстояния для идеального газа (а), реального газа (б), жидкостей (б) и кристалла ГЦК, (г)

Выясним, какой вид имеет функция W(R) для газов, кри­сталлов и жидкостей. Для га­зов, как было сказано выше, W(R) = 1, если R > 2r, где r — радиус частицы; W(R) = 0, если R £ 2r, так как r(R) = r_о на всех расстояниях, превы­шающих диаметр частицы. Для кристаллов характер измене­ния корреляционной функции в зависимости от расстояния совпадает с приведенным выше графиком изменения радиаль­ной функции распределения r(R).

Амплитуды колебаний ча­стиц в жидкостях гораздо боль­ше, чем в кристалле. При этом молекулы жидкости, участвуя в тепловом движении, беспрерывно обмениваются ближайшими «со­седями». Если проследить за поведением какой-либо частицы, то можно убедиться, что за время наблюдения она окажется на раз­ных расстояниях от данной частицы. Вследствие этого корреля­ционная функция W непрерывна. Она испытывает несколько за­тухающих колебаний относительно единицы. При расстоянии, пре­вышающем некоторое значение, корреляционная функция прак­тически равна 1, т. е. при этом исчезает порядок в размещении частиц. Это подтверждает факт, что в жидкостях нет дальнего порядка. Максимумы на кривой соответствуют более вероятным межмолекулярным расстояниям, минимумы — расстояниям, на ко­торых частицы бывают очень редко. Последовательность максиму­мов соответствует последовательности равновесных межмолекуляр­ных расстояний в жидкости и поэтому определяет характер ближ­ней упорядоченности. Кривые W(R) для газов (идеальный и ре­альный), жидкостей и соответствующих кристаллов приведены на рис. 1.12.

Сопоставляя функции W(R} для жидкости и кристалла, видим, что в кристалле максимумы этой функции разделены промежут­ками, где W(R) = 0, тогда как в жидкости кривая непрерывна.

Для экспериментального исследования строения жидкостей применяют облучение их рентгеновскими лучами, электронами или нейтронами. При этом рентгеновские лучи рассеиваются электронами атомов, электроны — ядрами атомов и нейтроны — магнитным полем атомов. Этими методами изучают зависимость интенсивности рассеянного излучения от угла, под которым про­изводится облучение. Теория методов, на которой мы не останав­ливаемся, позволяет связать интенсивность рассеивания с кор­реляционной функцией, т. е. по кривым интенсивности рассеива­ния излучения, направляемого под разными углами, можно экспериментально определить изменение корреляционной функции с увеличением расстояния.

Экспериментальные данные по изменению коррелятивных функ­ций металлов показали, что для плотноупакованных металлов в твердом состоянии характерно сохранение ближнего порядка, имеющего место в кристалле, и уменьшение координационного числа. Первый максимум на кривой радиального распределения находится практически на том же расстоянии, что и радиус пер­вой координационной сферы кристалла. Так, для меди в кристалле r₁ = 2,55 Å; первый максимум на корреляционной кривой находится на расстоянии 2,55 Å; для алюминия расстояния равны 2,86 и 2,94; для железа — 2,52 и 2,52; для цинка — 2,9 и 2,71 Å. Второй максимум на корреляционной кривой охватывает интер­вал расстояний, в который попадают радиусы второй, третьей и четвертой координационных сфер кристалла золота. Уменьшение координационного числа при плавлении плотноупакованных ме­таллов (например у алюминия с 12 до 10,8) связано с увеличе­нием объема при плавлении и возрастанием числа вакансий.

Для рыхлых, некомпактноупакованных в твердом состоянии металлов (висмут, олово, сурьма, галлий, кремний, германий и т. п.) также характерно малое отличие расстояния первого мак­симума на корреляционной кривой от радиуса первых координа­ционных сфер кристаллов (у висмута эти расстояния равны соответственно 3,25 и 3,09, у олова — 3,25 и 3,15, у сурьмы — 3,30 и 2,9 Å). Координационное число у этих металлов при плавлении увеличивается, что связано с уменьшением их объема (у висмута, например, координационное число увеличивается с 3 до 7,5 Å).

Таким образом, экспериментальные исследования подтверж­дают теоретические выводы о сохранении ближнего порядка кри­сталлов в жидких металлах и связи их строения со строением ис­ходного кристалла.

Как следует из сказанного выше, для определения радиаль­ной функции распределения необходимо знать корреляционную функцию. Об ее экспериментальном определении мы уже говори­ли. Математическое ее вычисление составляет предмет статистиче­ской физики жидкого состояния, одним из основателей которой можно признать выдающегося советского ученого академика Н. Н. Боголюбова. Рассмотрение этого вопроса выходит за пре­делы нашего курса.

1.1.5. ОСОБЕННОСТИ СТРОЕНИЯ ЖИДКИХ СПЛАВОВ

В отличие от чистых металлов, которые плавятся при фикси­рованной температуре, плавление и затвердевание сплавов осуществляется в некотором интервале температур. Температура, при которой начинается плавление или заканчивается затвердевание сплава, называется температурой солидуса Т_с. Температура, при которой заканчивается плавление или начинается затвердевание,. называется температурой ликвидуса Т_л. Выше температуры лик­видуса существует жидкий сплав, ниже температуры солидуса — твердый сплав. В интервале ликвидус — солидус, который может составлять более 100 °С и называется интервалом кристаллизации имеется двухфазное состояние, т. е. твердая и жидкая фазы со­существуют. Температура ликвидуса определяется условиями рав­новесия жидкого сплава данного состава с выделяющейся из него твердой фазой. Аналогично температура солидуса определяется условиями равновесия твердой фазы, отвечающей составу сплава, с жидкой фазой.

В процессе плавления сплава изменяется не только его тем­пература, но и химический состав находящихся в равновесии фаз. Как известно из курса «Металловедение», равновесие раз­личных фаз в сплавах характеризуется диаграммами состояния, связывающими концентрации фаз с температурой и давлением. Известно много типов диаграмм состояния, зависящих от раство­римости компонентов в жидком и твердом состояниях.

Вводимые в сплав компоненты могут растворяться в основном металле, образуя твердые растворы. При этом если область рас­творимости примыкает к чистому металлу, т. е. начинается с нулевой концентрации (на диаграмме «сигара» или ее участок на­чинается от чистого компонента), то при образовании раствора сохраняется тип кристаллической решетки основного металла (рис. 1.13, а). Если же область твердого раствора не примыкает к чистым металлам, то, как правило, образуется новая, более сложная, решетка (рис. 1.13, б). Если в этом случае интервал растворимости невелик, то образуются так называемые интер­металлические соединения, представляющие собой также твердые растворы со специфической решеткой.

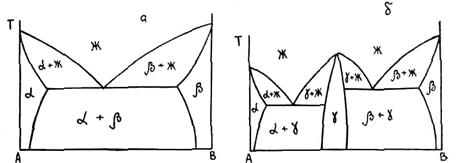
Рис. 1.13. Диаграммы состояния сплавов эвтектического типа без интерметаллидов (а) и с интерметаллидами (б)

Примеров интерметаллидов очень много, и часто именно они определяют механические и технологические свойства сплавов. Например, металлографию алюминиевых сплавов очень часто называют металлографией интерметаллидов. В качестве примера можно привести бинарные интерметаллиды CuAl₂, Mg₂Si, Mg₂Al₃ и т. д. Во многих случаях интерметаллиды могут быть многокомпонентными. Необходимо отметить, что часто и интерметаллиды могут образовывать твер­дые растворы с основным металлом.

Различают два типа твердых растворов: растворы замещения и растворы внедрения. В растворах замещения ионы легирующего компонента размещаются в узлах кристаллической решетки, за­мещая ионы основного металла-растворителя. Это имеет место тогда, когда размеры атомов компонентов близки друг к другу. Примерами растворов замещения являются растворы никеля в меди, цинка в меди и многие другие. Если размеры атомов силь­но различаются и атомы имеют разные строения электронных обо­лочек, например у металлов и неметаллов, то образуются раство­ры, внедрения (растворы бора, кислорода, азота). В них атомы растворенного вещества располагаются внутри кристаллической ячейки (в междоузлиях).

Введение легирующего компонента в раствор как при заме­щении, так и при внедрении искажает кристаллическую решетку, изменяет ее параметр и вызывает упругое напряженное состояние. Кроме того, легирующие компоненты оказывают влияние на ско­рость перемещения дислокаций.

Растворимость в твердом состоянии зависит от близости атом­ных диаметров компонентов, однотипности их кристаллических решеток и сходства строения внешних электронных оболочек. В соответствии с правилом Юма — Розери для образования не­прерывной растворимости различие в размерах атомов не долж­но превышать 15%. При больших различиях деформация решет­ки столь велика, что образование раствора становится термодинамически невыгодным.

При плавлении сплавов и металлов сохраняется ближний порядок (распределение атомов в первых координационных сфе­рах). Исследования показывают, что в жидком и твердом состояниях число атомов каждого сорта в первых координационных сфе­рах пропорционально их концентрации. Кривые интенсивности рассеяния излучений и радиальной функции распределения для сплавов напоминают аналогичные кривые для компонентов, отли­чаясь лишь координатами расположения максимумов. Максимумы располагаются между максимумами, характерными для чистых компонентов, и по мере увеличения компонента смещаются от одного компонента к другому. Если в твердом растворе атомы расположены статистически, т. е. неупорядоченно, то и в жидком сплаве сохраняется неупорядоченность, и наоборот, упорядочен­ность в расположении атомов в твердом растворе при плавлении сохраняется.

Статистическое распределение атомов в растворе имеет ме­сто, когда энергии парного взаимодействия атомов А и В связа­ны соотношением U_aa = U_bb = U_ab. В этом случае конфигурации А — А, А — В, В — В энергетически равноценны. В этих сплавах расстояние первого максимума на кривой радиального распреде­ления и координационное число линейно изменяются с увеличе­нием концентрации от значений этих величин для компонента А к их значениям для компонента В. При плавлении интерметаллидов, если между компонентами существует сильное взаимодейст­вие, сохраняется ближний порядок в расположении атомов, харак­терный для твердых интерметаллидов.

Эвтектические сплавы образуются из компонентов, различаю­щихся кристаллической решеткой и имеющих ограниченную рас­творимость в твердом состоянии. Этот тип сплавов чаще всего образуют металлы и неметаллы (например алюминий — кремний) и металлы с сильно различающимися параметрами решетки (на­пример медь с серебром). В этом случае силы взаимодействия между одноименными атомами больше, чем между разноименны­ми, т. е. U_aa > U_ab, U_bb > U_ab. Как показали исследования, при плавлении эвтектики расплав состоит из конфигураций, характер­ных для фаз a-твердого раствора и b-твердого раствора, состав­ляющих эвтектику. При повышении температуры происходит постепенное перемешивание атомов и образование однородного раствора. Квазиэвтектическая структура в расплаве может со­храняться при перегревах на 200—300°С.

Микронеоднородность жидких сплавов вызывается не только наличием кластеров, но и их различным составом, строением, ус­тойчивостью. Самые устойчивые кластеры образуются наиболее сильно взаимодействующими между собой компонентами. Как показали исследования Б. А. Баума, в бинарных железоуглеродистых сплавах возможно наличие следую-

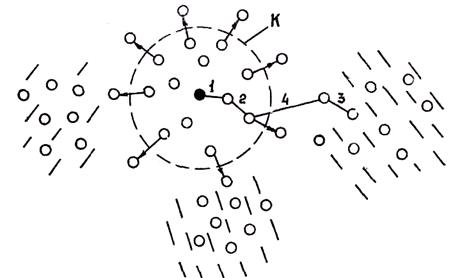
Рис. 1.14. Схема, иллюстрирующая микрунеоднородность железоуглеродистого сплава

щих кластеров. В распла­ве существуют межатомные связи Fe — Fe и Fe — С, при этом наиболее сильные — в сплаве Fe — С. Расплав представляет со­бой неоднородную систему, в которой межатомные связи Fe — Fe в микрообластях, удаленных от атомов примеси, и в непосредственной близости от них отличаются, так как атом углерода вы­зывает сильные искажения электронной плотности близко распо­ложенных атомов железной матрицы. На рис. 1.14 показана схе­ма микронеоднородной структуры железа, легированного углеро­дом. Темный кружок обозначает атом углерода; светлый кру­жок — атом железа; сплошные линии — межатомные связи, номер и длина которых обратно пропорциональны их прочности; заштрихованные области — кластеры типа объемно центрирован­ного куба; окружностью К. ограничен кластер, содержащий углерод.

В системе можно выделить четыре типа межатомных связей, которые в порядке убывания прочности обозначены цифрами 1 — 4. 1 — связь Fe — С внутри кластера, 2 — связь Fe — Fe вбли­зи атома С, 4 — связь между атомами железа в разных класте­рах, 3 — связь между атомами железа в кластере, удаленном от атомов С.

Эта схема характерна для еще не расплавленного сплава. При повышении температуры прежде всего разрываются меж­кластерные связи 4. Происходит предсолидусное плавление, разно­типные кластеры получают повышенную подвижность. При дости­жении температуры солидуса начинают разрываться связи 3. Од­нако эти связи разрываются не все одновременно, процесс раз­рыва одних связей сопровождается восстановлением других. При этом образуются кластеры, характерные для расплавов чистого железа (заштрихованные области). Этот кластер имеет ближний порядок, характерный для ОЦК. Вместе с этим кластером в расплаве имеется кластер, ограниченный окружностью К. Он имеет структуру ГЦК. Этот кластер обладает повышенной устой­чивостью, так как образован более сильными связями. При повы­шении температуры разрываются сначала связи 2, а затем свя­зи 1.

Реальные железоуглеродистые сплавы многокомпонентны. По­этому их микронеоднородность носит еще более сложный харак­тер.

1.1.6. ВЗАИМОСВЯЗЬ ЖИДКОГО И ТВЕРДОГО СОСТОЯНИЙ СПЛАВА

Свойства литого сплава в твердом состоянии определяются •свойствами жидкого сплава и условиями его охлаждения в форме. Связь с жидким состоянием сложна и многопланова. Поэтому в данном курсе мы не будем рассматривать ее всесторонне, пере­дав эту задачу технологическим курсам. Рассмотрим основные принципы, определяющие эту связь. Прежде всего, механические и другие свойства сплава в твердом состоянии в значительной мере определяются его кристаллической структурой. Процесс кристаллизации предполагает возникновение в жидком расплаве зародышей новой кристаллической фазы и ее рост. Зародышеобразование непосредственно связано с наличием в жидкости клас­теров и их характеристиками. Кроме того, большое значение имеет наличие в расплаве микроскопических включений различ­ного химического состава и строения. Определить их наличие невозможно никаким химическим анализом. Поэтому очень часто при смене поставщика шихтовых материалов при том же химсоставе выплавляемых сплавов существенно изменяются их свойства.

Зависимость свойств сплава от природы шихтовых материалов получила название «наследственность». Кроме неконтролируемого изменения содержания микропримесей наследственность можно объяснить неравновесностью жидкого состояния. Переход систе­мы, является самопроизвольно в течение времени релаксации. При плавлении металла расплав может находиться в неравновесном состоянии, т. е. состав и конфигурация образовавшихся кластеров не обладают минимумом энергии при данных условиях. Если вы­держать сплав при данной температуре достаточно долго, то в нем в конце концов установится равновесное состояние. О том, что время релаксации может быть достаточно большим, говорит хотя бы такой факт, что при вводе в расплав металлического феррохрома он не распределяется равномерно в нем даже через 20 мин.

Одним из доказательств неравновесности жидкого расплава является гистерезис свойств при нагреве и последующем охлаж­дении. Суть гистерезиса состоит в том, что значения свойств, по­лученные в измерениях в ходе нагрева сплава, не совпадают с соответствующими значениями, полученными при последующем его охлаждении. Повторные циклы измерений дают результаты, совпадающие с теми, которые получены при охлаждении сплава в первом цикле. На рис. 1.15 показан характер гистерезиса кине­матической вязкости сплава. Явление гистерезиса не обнаружи­вается, если сплав перед измерениями подвергнуть достаточной по длительности выдержке. Гистерезис свойств можно объяснить также какими-нибудь превращениями в сплаве при нагреве, свя­занными с выделением из него включений или продуктов взаимо­действия компонентов газовой среды или футеровки. Дискус­сии по вопросу, что здесь является главным, продолжаются. Од­нако можно несомненно признать, что неравновесность состояния сплавов имеет место и ее надо учитывать при организации тех­нологического процесса.

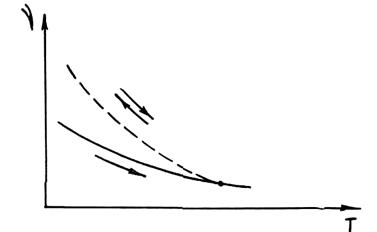
Рис. 1.15. Гистерезис кинематической вязкости

Для управления уровнем неравновесности состояния распла­вов сейчас широко применяют термовременную обработку.Приэтом расплав перед разливкой подвергается длительной выдерж­ке при температуре, несколько превышающей температуру за­ливки. Экспериментальные данные показывают, что при этом устраняется гистерезис свойств и существенно повышаются ме­ханические свойства литого сплава.

ГЛАВА 1.2. РЕОЛОГИЧЕСКИЕ СВОЙСТВА ЖИДКИХ И ТВЕРДЫХ СПЛАВОВ

Реология — наука, которая изучает деформации тел. Следует напомнить, что деформация—это изменение размеров и формы тела. Реология устанавливает связь между напряжениями, созда­ваемыми приложенными к телу силами, и вызываемыми ими де­формациями. В теории литейных процессов идеи реологии начали использоваться не более 10—15 лет назад. Для реальных физи­ческих объектов связь между напряжениями и деформациями мож­но выразить в виде следующего уравнения: F(t, e, e, eⁿ, t, t, ..., t^m) = 0.