Раздел 1. СТРОЕНИЕ И СВОЙСТВА ЖИДКИХ МЕТАЛЛОВ И СПЛАВОВ 4 страница

Изменение деформации в координатах деформация g — вре­мя t показано на рис. 1.33. Видно, что тело Гука обладает только мгновенно развиваемой обратимой, т. е. исчезающей после сня­тия напряжения, деформацией, равной g_H = ts. Сравнивая при­веденные кривые для сплава, можно заключить, что при t < t_S нет остаточной деформации, а при t > t_S появляется остаточная деформация. Поэтому можно сделать вывод, что искомое тело содержит тело Бингама. Кривые изменения деформации тела Бингама при нагрузке и разгрузке для t < t_s и для t > t_s приведены на рис. 1.33. Видно, что от экспериментальной кривой их отли­чает линейный характер зависимости. С целью придания зависи­мости нелинейного характера в тело нужно включить так назы­ваемое тело Кельвина, представляющее собой параллельно соеди­ненные тела Гука и Ньютона (рис. 1.34).

Приложенное к телу напряжение вычисляется по формуле t = t_H + t_N, где t_H—напряжение тела Гука, а t_N—напряжение тела Ньютона. Деформации параллельно соединенных тел равны g_H = g_N = g, g_H = t/s, g = t/h и t = gg + hg. Приняв t = const и преобразовав уравнение, получаем дифференциальное уравнение с разделяющимися переменными. Решаем его при начальном ус­ловии t = 0, g = 0.

;

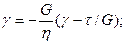
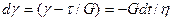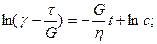
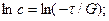
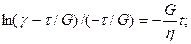
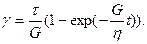
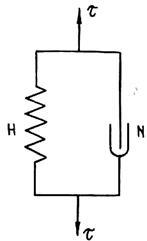
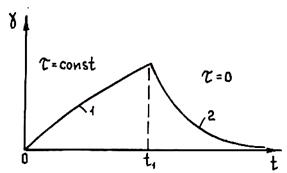
Рис. 1.34. Схема тела Кельвина (K-тела) Рис. 1.35. Поведение .К-тела при t-const (/) и при разгрузке (2)

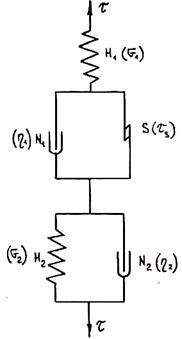
Рис. 1.36. Реологическая мо­дель сплава

Аналогично можно получить формулу для изменения дефор­мации при разгрузке (рис. 1.35). Видно, что в отличие от тела Гука в К-теле упругая деформация развивается не мгновенно. Легко убе­диться, что экспериментальная фор­ма кривой получится, если сложить кривые тел Гука, Бингама и Кельви­на. Деформации складываются при последовательном соединении тел. Та­ким образом, модель сплава имеет вид, показанный на рис. 1.36. Эта модель впервые была получена Г. Ф. Баландиным и Л. П. Каширцевым. Она описывает поведение спла­ва во всем интервале температур. При этом основные реологические харак­теристики сплава (модуль сдвига G₁, модуль упругого последействия G₂, пластическая вязкость h₁, псевдовяз­кость Кельвина h₂ и предельное на­пряжение сдвига t_S) зависят от тем­пературы. Характер некоторых из них приведен на рис. 1.31. Таким обра­зом, деформация сплава складыва­ется из гуковской упругой деформа­ции g₁, деформации упругого после­действия g₂ и пластической деформа­ции g₃, т. е. g = g₁ + g₂ + g Для вы­числения слагаемых можно написать следующие формулы:

; ;

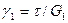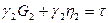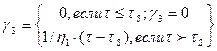
Относительный вклад указанных деформаций в общую дефор­мацию сплава зависит от температуры. В дальнейшем мы рассмотрим более подробно влияние реологической природы сплава на трещиноустойчивость сплавов в отливках.

ГЛАВА 1.3. ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ В МЕТАЛЛАХ И СПЛАВАХ

В различных технологических процессах плавки сплавов и получения отливок имеют место явления, происходящие на гра­ницах раздела жидких сплавов со шлаками, с газовой фазой и вакуумом, поверхностями песчаных и металлических форм, рафи­нировочными и защитными флюсами, газовыми включениями и т. п. Поверхностные явления оказывают большое воздействие на качество выплавляемых сплавов, процесс кристаллизации и формирование кристаллической структуры, химическую неодно­родность отливок, заполняемость форм, особенно для тонкостен­ных отливок, качество поверхности отливок и другие стороны ли­тейного процесса. В основе этого влияния лежит факт, что состоя­ние атомов в поверхностных слоях жидких сплавов существенно отличается от состояния атомов в объеме жидкости.

1.3.1. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКИХ МЕТАЛЛОВ

Частицы, находящиеся во внутренних слоях жидкости, окру­жены другими частицами и поэтому испытывают симметричные воздействия со всех сторон, которые компенсируют друг друга. В поверхностных слоях частицы испытывают нескомпенсирован­ные силовые воздействия притяжения со стороны ближайших «соседей», находящихся внутри жидкости.

Каждая частица, расположенная на поверхности жидкости, испытывает притяжение со стороны соседних внутренних частиц, направленное внутрь жидкости перпендикулярно ее поверхности. В связи с этим, для того чтобы перевести частицу из объема на поверхность, нужно совершить работу против сил притяжения. В результате энергия Гиббса поверхностных частиц больше, чем объемных, на величину указанной работы. Эта избыточная энер­гия Гиббса, отнесенная к единице поверхности жидкости на гра­нице с насыщенным паром или инертным газом, называется удельной свободной энергией (Дж/м²) или поверхностным натяже­нием s. При изотермическом процессе работа по увеличению по­верхности на dS равна dА = —sdS (знак «—» показывает, что работа при этом совершается не системой, а внешними силами над ней). Так как увеличение поверхности связано с возрастани­ем свободной энергии, то оно не может происходить самопроиз­вольно. С другой стороны, уменьшение поверхности снижает свободную энергию и может протекать самопроизвольно. Поэтому жидкость стремится принять конфигурацию с минимальной в дан­ных условиях поверхностью.

Силы поверхностного натяжения F направлены по нормали к любому элементу dl периметра поверхности жидкости и явля­ются касательными к ней. Численно поверхностное натяжение равно s = dF/dl. Его величину можно оценить по работе, затра­чиваемой против сил межчастичного взаимодействия при обрати­мом изотермическом разрыве столба жидкости сечением в еди­ницу площади, называемой когезией W_K. Очевидно, что в этом случае вместо одной фазы образуются две со своими поверхно­стями. Значит, W_K = 2s. Для большинства металлов характерно уменьшение поверхностного натяжения с увеличением молярного объема. Металлы отличаются большим по сравнению с неметал­лическими жидкостями поверхностным натяжением. Так, поверх­ностное натяжение калия — 102 мДж/м², цинка — 760, алюми­ния — 860, меди — 1350, магния — 560 и железа — 1860 мДж/м². Для сравнения у воды s = 75,5 мДж/м². Характерно увеличениеsс ростом температуры плавления металла. Обобщенно зависи­мость а от мольного объема и температуры плавления описывается формулой Шитила s = КТ_пл/V_ж^2/3 . Более точно ее можно вычислить по формуле s = 3,7×Т_пл/V_ж^2/3 + 140. Например, для желе­за s = 3,7×1 801×7,1/55,85 + 140 = 1 820 мДж/м² (здесь Т_пл имеет размерность К).

Большую величину поверхностного натяжения у металлов объясняют наличием в них свободных электронов. Значительную часть избыточной поверхностной энергии металлов составляет электростатическая энергия двойного электрического слоя, возни­кающего за счет выхода электронного газа за пределы металла.

С увеличением температуры поверхностное натяжение метал­лов убывает, стремясь к нулю при температуре абсолютного ки­пения. Коэффициент температурной зависимости s невелик и со­ставляет 0,07 мДж/(м²К) для калия, 0,65 — для цинка, 0,35 — для железа и 0,15 — для алюминия.

1.3.2. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ СПЛАВОВ

Сплавы представляют собой высокотемпературные растворы. В растворах силы взаимодействия между различными частицами неодинаковы, атомы и молекулы с более слабыми силовыми поля­ми вытесняются в поверхностный слой, так как это соответствует минимуму свободной энергии. Если добавляемый компонент по­нижает поверхностное натяжение растворителя, то он вытесняется в поверхностный слой, так как при этом уменьшается избыточная свободная энергия поверхностного слоя. Концентрация такого компонента на поверхности будет больше, чем в объеме. Этому будет препятствовать диффузия, стремящаяся выравнять кон­центрации. В результате устанавливаются некоторые равновесные значения концентраций на поверхности и в объеме.

Превышение поверхностной концентрации над объемной выражает уравнение Гиббса Г = -с/RT×(ds/dc)_Т. Видно, что; если ds/dc < 0 (поверхностное натяжение при увеличении концентра­ции компонента уменьшается), то Г > 0, т. е. концентрация в по­верхностном слое больше, чем в объеме. Такие вещества назы­ваются поверхностно-активными. В противном случае (поверх­ностное натяжение при увеличении концентрации компонента увеличивается, дs/дс > 0) компонент вытесняется с поверхности в объем. Такие вещества называются поверхностно-инактивными йо многих случаях поверхностная активность связана с различи^ ем атомных объемов растворителя и растворенного компонента ьсли атомные объемы сильно различаются, то растворенное ве­щество является поверхностно-активным. В случае, если атомные объемы компонентов близки, растворенное вещество является по-верхностно-инактивным.

Поверхностная активность играет большую роль в процессах кристаллизации. Кроме того, управление поверхностным натяжени­ем растворов в формовочных смесях позволяет воздействовать на такое их важное свойство, как текучесть.

Теория поверхностного натяжения растворов очень сложна и ее изложение выходит за рамки курса. Поэтому в заключение приведем фактические данные о влиянии легирующих компонентов на поверхностное натяжение сплавов на основе железа, алюминия и магния. Углерод, кремний, марганец, хром, фосфор, сера кисло­род, азот снижают поверхностное натяжение железа. При этом их поверхностная активность убывает в направлении S > O > Р > Mn > Si > C. Поверхностно-активными в железоуглеродистых сплавах являются следующие элементы, часто используемые как модификаторы, измельчающие зерно и управляющие его морфо­логией: цезий, кальций, натрий, цирконий, бор, алюминий. В чи­стых по сере сплавах магний является поверхностно-активным веществом. Однако если в сплаве есть кислород и сера, то маг­нии, раскисляя сплав (FeO + Mg = MgO + Fe) и переводя серу из раствора в сульфид магния (S + Mg = MgS), увеличивает s, так как кислород и сера — сильные поверхностно-активные примеси. Если магния в сплаве больше, чем нужно для раскисления и десульфурации, то избыточный магний растворяется в сплаве и понижает его поверхностное натяжение как поверхностно-актив­ное вещество. В качестве поверхностно-инактивных веществ мож­но привести титан, ванадий и молибден.

В алюминиевых сплавах поверхностно-активными добавками являются кремний, цинк, магний, натрий, литий. Введение даже сотых долей процента этих элементов приводит к сильному пони­жению s. Так, например, введение 0,1 % натрия снижает поверх­ностное натяжение с 849 до 619 мДж/м².

В магниевых сплавах поверхностно-активными являются вис­мут, свинец, сурьма, а поверхностно-инактивными — марганец, цинк, никель, германий.

1.3.3. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ. СМАЧИВАЕМОСТЬ

Форма, которую принимает свободная поверхность жидкости, зависит от сил поверхностного натяжения, от взаимодействия с ограничивающими поверхностями, а также от действующей на жидкость силы земного тяготения. Наблюдающиеся в этих слу­чаях явления получили название капиллярных. Они обусловлены тем, что благодаря действию сил поверхностного натяжения дав­ление внутри жидкости может отличаться от внешнего давления пара или газа на некоторую величину Р_к.

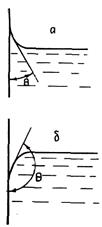
Рис. 1.37. Форма поверх­ности жидкости у Рис. 1.38. Форма капли жидкости на горизонтальной

верти­кальной стенки при сма­чивании (а) по­верхности при смачивании (а) и при несмачивании (б)

и при несмачивании (б)

Из физики известно, что Pк = s (1/R₁ + 1/R₂), где R₁ и R₂— главные радиусы поверхности. Если поверхность сферическая, то R₁ = R₂ = R и Р_к = 2s/R. Необходимо также учесть, что R > 0, когда поверхность выпуклая и R < 0, когда она вогнутая. Если молекула жидкости находится на границе с твердой стенкой со­суда, то она взаимодействует со своими ближайшими соседями как в жидкости, так и в стенке. Если молекула сильнее взаимо­действует с молекулами твердой стенки, чем с молекулами той же жидкости, то молекулы будут самопроизвольно переходить из объема на поверхность. При этом поверхность жидкости уве­личится, жидкость растечется по стенке, образуя каплю. На гори­зонтальной поверхности жид­кость растечется, на вертикаль­ной поверхности молекулы бу­дут «вползать» на стенку, обра­зуя вогнутый мениск. Так как при этом будет затрачиваться энергия на увеличение поверхно­сти, то при некотором угле q, называемом краевым углом, наступит равновесие. Угол q зави­сит от соотношения сил взаимодействия молекул жидкости с мо­лекулами стенки и между собой. При смачивании 0 £ q £ p/2 (рис. 1.37, а). При q = 0 имеем полное смачивание.

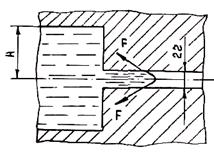
Рис. 1.39. Схема движения сплава в капилляре формы

Если силы взаимодействия между молекулами жидкости боль­ше, чем между жидкостью и твердым телом, то частицы будут переходить с поверхности в объем. Поверхность будет сокра­щаться, и картина контакта жидкости с вертикальной поверхно­стью будет иметь вид, показанный на рис. 1.37, б. При этом бу­дем иметь дело с несмачиванием. Краевой угол при несмачива­нии p/2 £ q £ p.

Следует отметить, что одно и то же тело может смачиваться одними жидкостями и не смачиваться другими. Например, стекло смачивается водой и не смачивается ртутью.

До сих пор мы рассматривали явления на границе двух тел — жидкости и твердого тела. Практически же мы всегда имеем вза­имодействие трех тел: жидкости, твердого тела и газа. На рис. 1.38 приведены схемы капель, лежащих на твердой под­кладке в газовой атмосфере. Кривая контакта этих трех тел в простейшем случае — окружность, обозначенная точками A и В. Приложим к точке А по касательным к поверхностям раздела соответствующих фаз силы поверхностного натяжения: s₁₂ — между жидкостью и подложкой, s₁₃ — между жидкостью и газом, s₂₃ — между газом и подложкой. Нетрудно видеть, что условие равновесия имеет вид s₂₃ = s₁₂ + s₁₃ × cosq, отсюда cosq = (s₂₃ — s₁₂)/ s₁₃.

С учетом смачивания и несмачивания рассмотренные выше яв­ления могут приводить к поднятию или опусканию жидкости в капиллярах. Для иллюстрации рассмотрим капилляр в песчаной форме, для простоты считая его цилиндрическим. Обычно неокис­ленный металл не смачивает форму, т. е. образует в капилляре выпуклый мениск. На рис. 1.3.9 показан капилляр на расстоянии H от уровня металла в форме. При этом со стороны сплава в направлении капилляра действует давление P_г = rgH. Капил­лярное давление Р_к = 2s×соs q/r в случае несмачивания действует в противоположном направлении, т. е. препятствует проникнове­нию металла в поры формы. Если металл окислен, то в зависи­мости от материала формы он может ее смачивать. При этом капиллярное давление направлено в ту же сторону, что и гидростатическое. Металл будет проникать в поры формы. Это приведет к пригару — образованию прочно сцепленного с поверхностью отливки пригарного слоя.

Для железоуглеродистых сплавов углы q имеют следующие значения: с кварцевым песком — 103°, с магнезитом — 113—126°, с хромомагнезитом — 102—112°, с хромистым железняком — 81—88°, с окисью алюминия — 141°. Видно, что в нейтральной атмосфере железоуглеродистые сплавы не смачивают основные формовочные материалы. Исключение составляет хромистый же­лезняк. Повышение содержания кислорода в железе резко уве­личивает смачивание. При увеличении содержания кислорода с 0,031 до 0,192% краевой угол q падает со 105,5 до 52°. Добавка к сплаву поверхностно-активных веществ (например серы к ста­лям и чугунам) вызывает уменьшение не только поверхностного натяжения, но и краевого угла. При этом эффект уменьшения q превышает эффект снижения s так, что капиллярное проникно­вение увеличивается.

Пористость формовочных смесей после уплотнения в форме составляет 15—45 %. При этом большая часть пор может быть отнесена к капиллярам. Капилляры в форме образуют сложную разветвленную пространственную систему неправильной геометри­ческой формы. Поэтому строгое описание капиллярного движения сплава наталкивается на большие трудности. Из рассмотренной выше схемы следует, что в случае смачивания сплавом формы проникновение будет происходить при любой величине гидроста­тического давления, при этом тем интенсивней, чем больше эф­фективный диаметр капилляра 2r_Э. Под эффективным диаметром капилляра будем понимать диаметр такого цилиндрического ка­нала, у которого высота капиллярного подъема сплава в данных условиях такая же, как в реальной форме. В случае несмачива­ния проникновение начнется только при Р_г > Р_к. Отсюда видно, что с ростом r_э давление проникновения Р_гп уменьшается.

Рассмотрим изотермическое проникновение сплава в капил­ляр в случае смачивания под действием только капиллярного давления.

Как известно из гидравлики, скорость капиллярного поднятия может быть описана формулой

v_ср = dl/dt = P_кr²/(8hl),

где Р_к = 2s cos q /r; r — радиус капилляра.

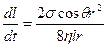или

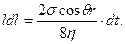
Интегрируя это уравнение при начальном условии t = 0, I = 0, находим формулу для вычисления зависимости глубины про­никновения сплава в форму от времени под действием капилляр­ного давления:

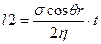или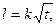

где k = .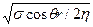

Из формулы видно, что глубина изотермического проникно­вения сплава пропорциональна V~ t. Величина k для окисленной стали имеет порядок 0,1—0,3 мм²/с. В реальных условиях проник­новение сплава неизотермическое. Установлено, что длина про­питанного слоя фактически определяется не гидравлическими условиями, а условиями прогрева слоя формовочных материалов. Для течения необходимо, чтобы смесь перед головой капилляр­ного потока успевала прогреться до температуры ликвидуса сплава. Следует, однако, отметить, что в реальной форме чисто капиллярной пропитки не происходит, так как гидростатическое давление сплава в форме даже для ее верхних участков имеет тот же порядок, что и капиллярное давление.

1.3.4. СИЛЫ АДГЕЗИИ И КОГЕЗИИ

Рассмотрим контакт двух фаз (жидкой и твердой или двух твердых). Поверхностные натяжения фаз обозначим s₁ и s₂, а межфазную энергию фаз на границе их раздела — s₁₂. Работу их изотермического обратимого разделения можно вычислить по формуле W_A = s₁ + s₂ - s₁₂. Эта работа называется адгезией. Поверхностное натяжение твердых фаз определить трудно. По­этому используем данные о смачивании этих поверхностей жид­костями. Рассматривая адгезию жидкой 1 и твердой 2 фаз, найдем экспериментально краевой угол смачивания твердой фазы данной жидкостью. Он равен cos q = (s₂ — s₁₂)/s₁. Поэтому w_a = s1(1 + cos q). Адгезия является характеристикой прочности сцепления фаз. Она тем больше, чем выше поверхностное натя­жение контактирующих фаз и меньше их межфазное натяжение. Из полученного выше выражения следует, что, чем выше (s₁ и чем лучше жидкость смачивает твердое тело, тем прочнее их сцепле­ние. Адгезия чистого жидкого железа к магнезии — 360 мДж/м². С увеличением окисленности железа (q уменьшается) адгезия резко возрастает (до 1235 мДж/м²). Величина адгезии опреде­ляет энергетические затраты на удаление приставшего к отливке пригарного слоя.

Как было сказано выше, работа по разрыву фазы с образо­ванием двух новых поверхностей раздела, равная 2s, называется когезией. Соотношение между адгезией воды, содержащейся в смеси, к поверхности модели или стержневого ящика и когезией смеси определяет прилипаемость смеси к модельной оснастке. Если смесь прилипает к поверхностям модели или ящика, то качествен­ную форму или стержень приготовить невозможно. Для исключе­ния прилипания необходимо, чтобы когезия превышала адгезию. Основные меры борьбы с прилипаемостью рассматриваются в курсе «Технология литейного производства».

1.3.5. РОЛЬ ПОВЕРХНОСТНЫХ ЯВЛЕНИЙ В ПРИГАРООБРАЗОВАНИИ НА ОТЛИВКАХ

Процесс затвердевания отливки в литейной форме связан с формированием ее поверхности, контактирующей с поверхностью формы. Как было сказано выше, форма представляет собой ка­пиллярно-пористое тело, имеющее сложные по конфигурации ка­пилляры, более или менее открытые для проникновения в них жидкого металла из полости формы. При этом на проникающий в капилляры жидкий металл действуют следующие силы:

а) гидростатическое давление столба жидкого металла в фор­ме Р_г;

б) капиллярное давление, приложенное к свободной поверх­ности жидкого сплава в капилляре, Р_к;

в) избыточное давление газов в порах смеси, образующееся при окислении, испарении и деструкции ее составляющих в про­цессе прогрева формы при заливке и охлаждении сплава, Р_гф.

Схема приложения сил к расплаву в капилляре при смачива­нии формы металлом показана на рис. 1.40. Очевидно, что для проникновения сплава в форму необходимо выполнение неравен­ства Р_г + Р_к > Р_гф. При этом следует иметь в виду, что в целях борьбы с газовыми дефектами в отливках состав смеси подбирают так, чтобы она была наименее газотворна, т. е. добиваются мннимального уровня давления Р_гф. Таким образом, смачивание жид­ким сплавом формы, как правило, ведет к его проникновению в межзеренные капилляры смеси. В случаях несмачивания сплавом формы Р_г > Р_к + Р_гф. Условия, исключающие его проникновение, выполнить проще, но также не всегда возможно.

Если указанные условия проникновения выполнены, то при изотермическом процессе расплав в капилляре под действием перепада давлений будет двигаться как угодно долго. При этом длина заполненного капилляра будет увеличиваться, как было показано выше, пропорционально V~ t.

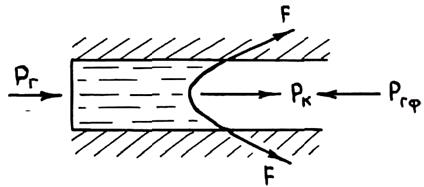
Рис. 1.40.Распределение давлений при смачивании сплавом формы

В условиях реальной песчаной формы проникновение сплава в капилляры происходит в неизотермических условиях. В песча­ной форме после заливки сплава температура распределена не­равномерно, по мере удаления от границы с отливкой она быст­ро убывает. Поэтому голова потока расплава в капилляре все время набегает на холодные, непрогретые поверхности зерен пес­ка, что приводит к затвердеванию прожилок расплава и прекра­щению его проникновения. Обычно глубина проникновения рас­плава ограничивается одним или несколькими слоями зерен смеси. Однако в некоторых случаях, особенно в тонких центральных, со всех сторон омываемых сплавом стержнях, металл может запол­нить капилляры на всю толщину стержня. В этих случаях проис­ходит, как говорят, сквозная металлизация стержня. Такой стер­жень практически невозможно выбить из отливки.

В результате поверхностного проникновения металла в поры смеси на поверхности отливки образуется и удерживается после выбивки более или менее толстый слой пропитанной металлом формовочной смеси, иногда очень трудноудалимый. Этот поверх­ностный дефект отливок называют пригаром. Пригар, образуемый по описанному механизму, называется механическим пригаром.

Однако на практике чисто механический пригар образуется редко. В условиях окислительной атмосферы формы поверхность металла часто покрыта пленками окислов. Например, при литье железоуглеродистых сплавов важную роль играют окислы железа и марганца FeO и МпО. С кремнеземом песка эти окислы всту­пают во взаимодействие с образова­нием легкоплавких соединений типа файялита (2FeO×SiO₂), родонита (MnO×SiO₂), тефроита (2MnO×Si0₂) и др. С возникновением окисных или силикатных легкоплавких фаз про­никновение сплава в поры смеси су­щественно облегчается. Окислы хоро­шо смачивают смесь и сами хорошо смачиваются металлом. Расплав идет за ними в капилляр как нитка за иголкой. Следует заметить, что окисные расплавы легко пропитывают по­верхностный слой смеси, химически разрушая зерна песка. Иногда вме­сто зерен песка в пригарном слое об­наруживают монолитную массу, со­стоящую из указанных выше соеди­нений. При этом образуется наиболее тяжелый вид пригара — химический. Из изложенного следует, что необходимой стадией химического пригара являются процессы, связанные с механическим пригаром. Схема образования пригарного слоя показана на рис. 1.41. К описанным выше процессам следует добавить процессы плавления наиболее легкоплавких составляющих смеси (окислы щелочных металлов, зерна поле­вого шпата, алюмосиликаты глины и т. п.) и их последующего спекания. Эти процессы характерны для так называемого терми­ческого пригара.

Все указанные виды пригара, как правило, сосуществуют. Пригарный слой представляет собой самостоятельную фазу, име­ющую свою структуру. Этот слой удерживается на поверхности отливки не только за счет действия проникших в смесь прожилок металла, но и за счет адгезии, чему способствуют спекание слоя и структурные превращения в нем. Для уменьшения адгезии не­обходимо повысить межфазное натяжение на границе поверхность отливки — пригарный слой. В тех случаях, когда межфазное натя­жение на этой границе мало, что имеет место при близких струк­турах металла и слоя, пригарный слой прочно удерживается на поверхности отливки силами адгезии.

Для примера можно привести неожиданный результат, полученный при освоении жидкостекольных смесей на УЗТМ в начале 50-х гг. Данные смеси, связующим в которых является силикат натрия или калия, содержат большое количество легкоплавких окислов щелочных металлов и поэтому отличаются большой пригораемостью. К удивлению технологов, смеси относительно легко были внедрены на стальном литье. При этом образовывался до­статочно толстый слой пригара, который легко отскакивал от поверхности отливок при их очистке. В то же время на чугунном литье, несмотря на значительно меньшую, чем при стальном литье, температуру заливки, при применении жидкостекольных смесей образуется трудноудалимый от поверхности отливки пригарный слой. Минералогический и рентгеноструктурный анализ пригарного слоя показали, что при температурах, характерных' для литья чугуна, он имеет кристаллическую структуру, близкую к структуре металла. Это приводит к снижению межфазного натя­жения на границе отливка — пригарный слой и, как следствие, к увеличению адгезии. При литье стали пригарный слой имеет вид аморфно-стекловидной массы, что приводит к увеличению межфазного натяжения и снижению адгезии.

Таким образом, поверхностные явления играют важную роль в пригарообразовании. Естественно, такой сложный процесс не исчерпывается только поверхностными явлениями. Комплексное рассмотрение пригарообразования — предмет технологических раз­делов спецкурса. С точки же зрения поверхностных явлений борь­ба с пригаром должна быть направлена на уменьшение как смачиваемости металлом материала формы, так и адгезии слоя к сплаву. Это может достигаться соответствующим подбором формо­вочных материалов, противопригарных покрытий, раскислением металла, предотвращением его окисления в форме, соответствую­щим легированием сплава и т. п.