Раздел 2. ОСНОВЫ ТЕОРИИ ФОРМИРОВАНИЯ КРИСТАЛЛИЧЕСКОЙ СТРУКТУРЫ ОТЛИВОК 2 страница

При атомно-гладкой поверхности зародыша (рис. 2.10, а) воз­можен только послойный рост кристалла путем образования на гранях двумерных зародышей, которые разрастаются

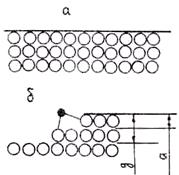
Рис. 2.10. Типы морфологии по­верхности растущего Рис. 2.11. Рост кристалла путем присоединения

кристалла: а — атомно-гладкая поверхность; отдельных ато­мов (а) и двумерных зароды­шей (б)

б — ограненная поверхность

затем вдоль этих граней. Рост путем присоединения отдельных атомов в данном случае энергетически неустойчив, так как каж­дый адсорбированный поверхностью атом имеет только одного ближайшего «соседа» и, следовательно, только одну связь (рис. 2.11, а). В таких условиях он не может устойчиво закре­питься на поверхности. Поэтому рост может происходить только путем образования и закрепления тонких, одно-, двух- и трехатом­ных по толщине, плоских образований атомов, называемых дву­мерными зародышами.

На рис. 2.12 приведена схема двумерного зародыша на грани растущего кристалла. При образовании такого зародыша поверх­ность кристалла увеличивается на ΔS = 4×2x×d = 8x×d, т. е. на величину поверхности четырех боковых граней. Соответствующее возрастание поверхностной энергии равно A_s = 8xds = 8×xs', где s' = `ds — поверхностная энергия, приходящаяся на единицу пери­метра зародыша толщиной d. Если энергию Гиббса зародыша с основанием 1 см² обозначить j₂, а энергию Гиббса, приходящую­ся на то же число атомов жидкости, — j₁, то для полного измене­ния энергии при зародышеобразовании можно написать следую­щее выражение:

.

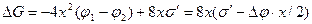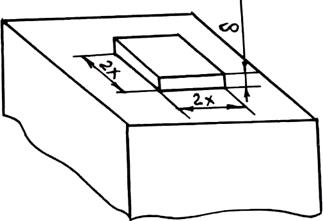
Рис. 2.12. Схема образования двумерного зародыша на грани кристалла

Подставив в это выражение Δj = j₁ — j₂ = ΔH`×ΔT/Т_кр (см. гл. 2.1), где ΔH' — теплота плавления зародыша с основанием 1 см², получаем

.

; .

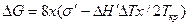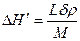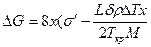Исследуем эту зависимость на экстремум:

.

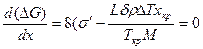Из этого уравнения находим выражение для вычисления критиче­ского размера зародыша х_кр, при котором ΔG достигает максимума:

.

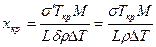Работа образования этого зародыша вычисляется по формуле

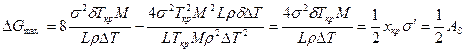
Сравнение полученных формул для вычисления размера и работы образования двумерного критического зародыша с соот­ветствующими выражениями для трехмерного зародыша (см. гл. 2.1) показывает, что критический размер двумерного зародыша в 2 раза меньше, чем трехмерного, меньше и работа образования критического двумерного зародыша. Вероятность образования в единице объема двумерного зародыша равна

.

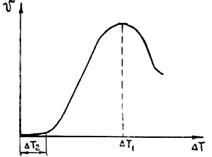
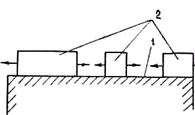
Рис. 2.13. Зависимость линейной ско­рости Рис. 2.14. Схема одновременного ро­ста нескольких

роста кристалла от переохлаж­дения двумерных зароды­шей:

/—грань кристалла; 2—зародыши

Вероятность присоединения к зародышу в единицу времени хотя бы одного атома равна р₂ = с₂×ехр(—U/kT). Вероятность образо­вания центра кристаллизации вычисляется по формуле

,

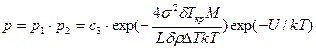где с₃ = с₁×с₂ — некоторая постоянная для данного вещества ве­личина.

Скорость роста кристалла пропорциональна вероятности р, т. е.

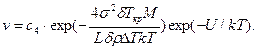
Характер зависимости линейной скорости роста от переохлажде­ния ΔТ показан на рис. 2.13.

Величина интервала метастабильности при росте кристаллов ΔТ₂ значительно меньше, чем ΔТ₁ при зарождении. При этом, как правило, реализуется только восходящая ветвь кривой (см. рис. 2.13). Зависимость можно аппроксимировать следующей функцией:

,

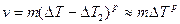где показатель степени 1 £ р £ 2. Двумерный зародыш быстро растет, последовательно присоединяя к своим боковым граням ряды атомов так, что слой, образованный зародышем, покрывает грань кристалла. После заполнения грани наступает пауза, дли­тельность которой t ~ ехр(4s`х_кp/kT) обратно пропорциональна вероятности р₁. Затем наращивается новый слой и т. д. У кубиче­ского кристалла в идеальном случае все шесть граней переме­щаются с одинаковой скоростью в направлениях своих нормалей.

Когда грань кристалла достаточно велика, длительность ее заполнения t значительно больше времени ожидания появления нового зародыша t. В этом случае возможны образование и не­зависимый рост двух или нескольких зародышей (рис. 2.14).

2. На атомно-шероховатых поверхностях кристаллов могут надежно адсорбироваться отдельные атомы жидкости (рис. 2.10, б). При этом происходит так называемый нормальный рост кристал­лов, когда атомы расплава беспорядочно присоединяются к лю­бым точкам поверхности. В этом случае грань кристалла пере­мещается однородно по нормали к самой себе. Соответствующий расчет показывает, что линейная скорость роста в данном случае пропорциональна переохлаждению:

,

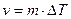где m = n×L×M×exp(—U/kT)/(T²_nep×R); R — универсальная газо­вая постоянная; n — частота колебаний атомов в жидкости.

3. Механизм роста существенно изменяется, если на поверх­ности растущего кристалла имеются какие-нибудь выступы, ко­торые облегчают закрепление частиц жидкости на поверхности кристалла. Очень часто такие выступы образуются в местах вы­хода винтовых дислокаций. Кристаллы, на гранях которых име­ются ступеньки, возникшие в результате выхода винтовых дисло­каций, растут послойно путем присоединения атомов расплава к этим ступенькам. Не приводя вывода, запишем формулу для вы­числения линейной скорости в этом случае:

,

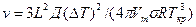где s — межфазное натяжение на границе кристалл — жидкость; V_m — молярный объем жидкости; Д — коэффициент диффузии.

Из формулы видно, что линейная скорость роста v пропорцио­нальна (ΔT)². Дислокационный послойный рост происходит при значительно меньших переохлаждениях, чем рост двумерных за­родышей. Интервал метастабильности по росту в этом случае ра­вен нулю.

На рис. 2.15 приведены результаты исследования механизма роста в зависимости от величины переохлаждения на фронте крис­таллизации. Видно, что при малых переохлаждениях рост осуществляется путем образования двумерных зародышей, при боль­ших переохлаждениях

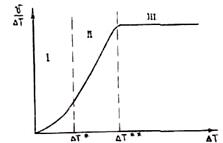
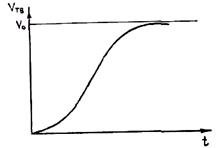
Рис. 2.15. Зависимость механизма ро­ста кристаллов от Рис. 2.16. Кинетическая кривая криcталлизации

величины пере­охлаждения на фронте кристаллиза­ции:

I — зона образования двумерных зароды­шей;

II — промежуточная зона;

III — зона нормального роста кристаллов

— по нормальному механизму. При этом фронт не огранен, т. е. имеет вид атомно-шероховатой поверхно­сти. В промежуточной зоне переохлаждения рост может осущест­вляться по дислокационному механизму. В реальных условиях литья, как правило, реализуется нормальный механизм роста.

ГЛАВА 2.4. КИНЕТИКА КРИСТАЛЛИЗАЦИИ. ФОРМУЛА КОЛМОГОРОВА

Рассмотренные выше характеристики процесса кристаллиза­ции—скорость возникновения центров кристаллизации п и ли­нейная скорость роста кристаллов v — являются важнейшими кристаллизационными характеристиками, определяющими кинетику кристаллизации. Математической величиной, описывающей кинетику кристаллизации, является временная зависимость объ­ема закристаллизовавшейся жидкости.

Решение задачи о кинетике нарастания твердой фазы при кри­сталлизации было впервые выполнено А. Н. Колмогоровым. Ис­пользуя аппарат теории вероятности, можно получить следующую формулу:

,

где n(t) = v(т) — скорость возникновения центров кристаллиза­ции и линейная скорость их роста как функции времени; V₀ — на­чальный объем расплава. Формула справедлива для сферического зародыша. Если принять в ней n = const и v = const, то после ин­тегрирования нетрудно получить формулу Колмогорова

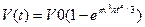. (2.3)

Графически она описывается кривой, показанной на рис. 2.16. Видно, что на начальных и конечных временных участках наблю­дается незначительный темп нарастания твердой фазы. Замедле­ние кристаллизации в конце объясняется тем, что растущие кри­сталлы начинают соприкасаться друг с другом при малом и не­прерывно уменьшающемся количестве жидкости. Так как в кон­це кристаллизации объем жидкости мал, то основное положение вывода V₀ >> V_кр не соблюдается. Поэтому из формулы вытекает неправдоподобный результат, что продолжительность полного за­твердевания объема равна бесконечности. При этом погрешность формулы тем больше, чем меньше кристаллов и чем больше раз­мер зерна. Принято считать, что формула обеспечивает расчет с погрешностью не более 1 %, если выполняется условие V₀(n/v)^3/4 > 200. Анализ показывает, что это условие, как правило, соблюдается при затвердевании реальных сплавов.

В обобщенном виде уравнение кинетики кристаллизации мож­но записать следующим образом:

,

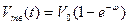где 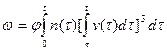; (j — коэффициент, учитывающий конфигурацию кристаллита (j = 4p/3 для шара и j = 8 для кубических кристаллитов).

Рассмотрим кинетику кристаллизации при объемном затверде­вании. Возьмем некоторый объем сплава Vo, который охлаждает­ся при малой интенсивности теплообмена с внешней средой. В этих условиях можно пренебречь перепадом температур по объ­ему и рассматривать, что кристаллизация происходит путем равно­мерного выделения по всему объему твердой фазы. Такое затвер­девание называют чисто объемным. Пусть при t = 0 температура расплава равна T = T_кр—ΔT₁, где ΔT₁ — интервал метастабильности по зарождению кристаллов. Напишем уравнение теплового баланса:

,

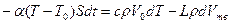где a — коэффициент теплоотдачи с наружной поверхности объ­ема; S — поверхность охлаждения; T₀—температура среды; L, с и р — удельная теплота кристаллизации, теплоемкость и плотность расплава; V_тв — объем металла, затвердевшего за время t; dT—изменение температуры за время dt. Для оценки зависимо­сти параметров п и v от переохлаждения примем v = mΔT = m(T_кр – T), n = n₀(ΔT – ΔT₁)² = n₀(T_кp – T – ΔT_l)² приΔT>ΔT₁ и n = 0, если ΔT £ ΔT₁. Проинтегрируем это уравнение при начальном условии: при t = 0 V_тв = 0 и T = T_кр – ΔT₁. Кроме того, в левой части уравнения примем T = Т_кр ввиду малой величины переохлаждения ΔT при кристаллизации металлов.

,

Подставив в это уравнение выражение для V_тв (см. форму­лу Колмогорова), получаем интегральное уравнение, описывающее изменение температуры металла при его объемной кристал­лизации:

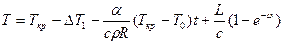. (2.4)

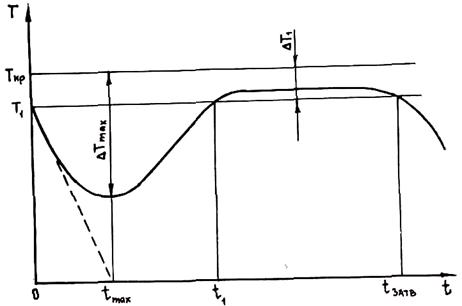
Рис. 2.17. Изменение температуры расплава при его объемной кристаллизации

Решить это уравнение возможно только с применением численных методов на ЭВМ. Изменение температуры во времени показано на рис. 2.17 (расчетные данные). Подобный характер температур­ной кривой подтверждается многочисленными экспериментами.

Если бы в расплаве не выделялась теплота кристаллизации, то температура уменьшалась бы в соответствии со штриховой линией на рис. 2.17, которая отвечает уравнению T = T_кр – ΔT₁ - (Т_кр – Т₀)×t×a /(c×r×R). Однако выделяющаяся теплота кристал­лизации замедляет темп охлаждения, и в момент t = t_max dT/dt = 0, что соответствует минимуму температуры, или максимуму переохлаждения (ΔT = T_кр – Т). При t > t_max dT/dt > 0, а темпе­ратура сплава повышается, пока переохлаждение не станет мень­ше интервала метастабильности по зарождению ΔT₁. При t > t₁ ΔT < ΔТ₁ и зарождение новых кристаллов в расплаве прекраща­ется. Далее будет происходить только рост образовавшихся в пе­риод 0 < t < t₁ центров до полного затвердевания металла при t = t_затв. Этот подъем температуры называется рекалесценцией.

Приближенное решение уравнения, выполненное с использо­ванием метода итераций, позволило получить следующие фор­мулы для расчета параметров температурной кривой:

;

;

; ; .

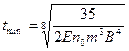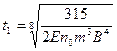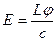Для вычисления количества центров кристаллизации, зародив­шихся на первом этапе кристаллизации, получена следующая при­ближенная формула:

,

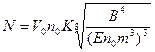где К » 3,5.

Расчеты на ЭВМ и эксперименты показали достаточную точ­ность этих формул.

Величина N фактически определяет число кристаллических зерен в затвердевшей отливке, так как при t > t₁ новые зерна не зарождаются. Приняв, что V₀ = Npd³/6, где d — эффективный диа­метр зерна, с учетом формулы для вычисления N легко найти следующее выражение для оценки величины кристаллического зерна при объемной кристаллизации:

,

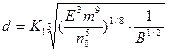где K₁ = .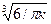

Из полученной формулы видно, что для измельчения зерна необходимо увеличить СВЦК. n₀ и уменьшить линейную скорость роста т. Видно, что зерно измельчается при повышении коэф­фициента теплоотдачи а и снижении удельной теплоты кристал­лизации L.

Рассмотренная выше схема чисто объемной кристаллизации, когда твердая фаза растет от отдельных центров во всем объеме жидкости, может быть реализована для чистых металлов при малом значении критерия Био (Bi = aR/l), т. е. при малых зна­чениях a и R. При Bi > 0,l, как правило, объемная кристаллизация в центральных объемах сопровождается последовательным про­движением затвердевшей корки с поверхности охлаждения спла­ва к центру отливки. При объемной кристаллизации величина максимального переохлаждения ΔT_mах невелика (для алюминия не более 1—5°С, для железа — до 40 °С). Длительность первого этапа (t £ t₁) составляет относительно небольшую долю от об­щего времени затвердевания. Как правило, мы измеряем термо­парой температуру сплава на втором этапе затвердевания, когда переохлаждение (ΔT < ΔT₁) очень мало. При этом температура, фиксируемая термопарой, близка к Т_кр.

Изложенная теория показывает, какое большое значение для управления формированием кристаллического строения отливки кроме теплового режима имеет целенаправленное воздействие на кристаллизационные параметры п и v.

ГЛАВА 2.5. ПЕРЕРАСПРЕДЕЛЕНИЕ ПРИМЕСЕЙ НА ФРОНТЕ КРИСТАЛЛИЗАЦИИ СПЛАВОВ. ВНУТРИКРИСТАЛЛИЧЕСКАЯ ЛИКВАЦИЯ

При кристаллизации сплавов концентрации компонентов в фа­зах, находящихся в равновесии, как правило, различаются. Отно­шение концентраций компонента в находящихся в равновесии твердой и жидкой фазах k₀ = C_S/C_L. называется равновесным ко­эффициентом распределения. На рис. 2.18, а приведен участок диаграммы состояния сплава, температура ликвидуса которого уменьшается с увеличением концентрации легирующего компо­нента В. Очевидно, что в этом случае коэффициент распределе­ния k₀ < 1 (обычно 0,2 £ k₀ £ 0,6).

При повышении температуры ликвидуса (рис. 2.18, б) коэф­фициент распределения k₀ > 1. Обычно в этом случае k₀ < 3. Од­нако, например, в системе Ge — В k₀ достигает 15.

Дальнейшее изучение кристаллизации будем проводить при k₀ < 1, так как эта величина является характерной для большин­ства литейных сплавов.

Рассмотрим несколько частных случаев.

1. Скорость роста кристалла настолько мала, что диффузия успевает выравнять концентрации вещества по объему твердой и жидкой фаз. При этом концентрации будут соответствовать равно­весным значениям, определенным для данной температуры по диаграмме состояния. На рис. 2.19 показано распределение кон­центрации по длине твердой и жидкой фаз. Ось ординат, которая

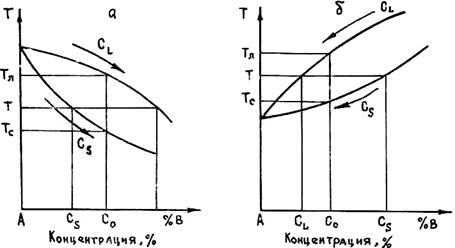
Рис. 2.18. Диаграммы состояния сплавов с понижением (а) и повышением (б) температуры ликвидуса в зависимости от роста концентрации легирующего ком­понента

соответствует концентрации, является подвижной и совпадает с положением фронта кристаллизации. В этом случае k₀ = С_S/С_L.

2. Ситуация, более приближенная к реальной, имеет место, когда в твердой фазе при данной скорости роста кристалла не происходит диффузионного перераспределения вещества (Д_тв = 0). Однако в жидкости, вследствие интенсивного перемешивания расплава, концентрации выравниваются. Так как Д_тв = 0, то со­став твердой фазы, образовавшийся на предыдущих стадиях, остается неизменным. Так как при k₀ < 1 по мере кристаллизации C_S увеличивается (см. рис. 2.18, а), то концентрация вещества будет возрастать по длине твердой фазы, оставаясь на фронте кристаллизации равной соответствующему значению, определен­ному по диаграмме состояния. Распределение концентраций по длине фаз в рассматриваемом случае приведено на рис. 2.20. Так как концентрация жидкости c_l больше концентрации твер­дой фазы на фронте кристаллизации C_S, то при затвердевании жидкости на фронте кристаллизации выделяется легирующий ком­понент. Например, если за время dt затвердевает dm жидкости, то количество выделившегося вещества равно (C_l—C_S)dm. В дан­ном случае это вещество равномерно распределяется по объему жидкости.

Явление, связанное с неравномерным распределением концент­рации вещества, называется ликвацией. В рассматриваемом слу­чае наблюдается максимальная ликвация в твердой фазе, назы­ваемая внутрикристаллической ликвацией. При этом внутренние слои сферического

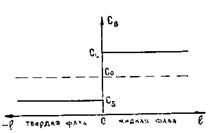
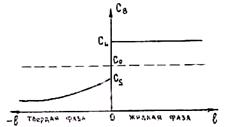
Рис. 2.19. Распределение концентра­ции по длине Рис. 2.20. Распределение концентра­ций по

жидкой и твердой фаз при малой скорости длине фаз при Д_тв = 0 и Д_ж ® ¥

кристаллизации (k₀ < 1)

кристаллита будут иметь меньшую концентрацию легирующего компонента, чем поверхностные (при слои сферического k₀ < 1). Сред­нее содержание вещества в твердой фазе будет всегда меньше определенного по диаграмме состояния, а в жидкости, наоборот, средняя концентрация превысит равновесные значения. Это при­ведет к смещению влево линий солидуса на диаграмме состояния. Положение равновесной и неравновесной линии солидуса пока­зано на рис. 2.21. Неравновесная линия солидуса отвечает сред­ним значениям концентрации компонента в твердой фазе. Из рис. 2.21 видно, что при равновесной температуре солидуса Т_{сол. р} часть жидкости остается незатвердевшей. Массовую долю этой жидкости можно найти по правилу рычага. Она равна отно­шению отрезков ae/ab. Полное затвердевание жидкости произой­дет при более низкой температуре неравновесного солидуса T_сол.н.р, которая ниже равновесного значения на величину отрез­ка ΔT = ес.

Для выравнивания концентрации по объему кристаллитов при­меняют гомогенизационный отжиг, т. е. выдержку сплава при по­вышенных температурах, при которых значение коэффициента диффузии Д_тв достаточно для диффузионного относительно быст­рого выравнивания концентраций. Так как при перемешивании жидкости вещество, выделившееся на фронте затвердевания, от­водится и равномерно распределяется по ее объему, то в этом случае k₀ = С_S/С_L.

3. При переходе к более высоким скоростям роста, которые обычно имеют место, реализуется диффузионно контролируемый режим кристаллизации. Перенос вещества с фронта кристалли­зации в объем жидкости осуществляется путем диффузии, и рас­пределено оно в ней неравномерно. Примесь, выделяющаяся при образовании твердой фазы (k₀ < 1), накапливается у движуще­гося фронта кристаллизации, и ее концентрация на фронте С_L0 превышает концентрацию в объеме С_L (рис. 2.22). В данном слу­чае k₀ = C_S/C_L0.

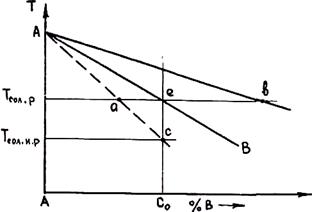
Рис. 2.21. Положение равновесной и неравновесной ли­ний солидуса на диаграмме состояния сплава

В процессе перемещения фронта кристаллизации концентра­ция С_L0 повышается, потому что не вся примесь отводится в рас­плав. Это приводит к увеличению концентрации растворенного вещества как в жидкости, так и в твердой фазе. При некотором положении фронта кристаллизации концентрация в твердой фазе достигает С₀, а в расплаве на фронте — С_L0 = С₀/k₀. Соответствую­щее этому моменту распределение концентраций показано на рис. 2.23.

В этих условиях можно написать следующее уравнение балан­са вещества для фронта кристаллизации:

.

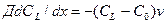Здесь выражение в левой части определяет количество веще­ства, отведенного от фронта в расплав, а выражение в правой части — количество вещества, выделившегося при кристаллизации. Проинтегрировав это уравнение при начальных условиях x = 0, C_L =C₀/k , получаем выражение, описывающее распределение кон­центрации примеси в расплаве вблизи фронта кристаллизации:

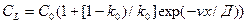. (2.5)

На некотором расстоянии х = d c_l практически равно С₀. Вели­чина d называется толщиной диффузионного пограничного слоя.

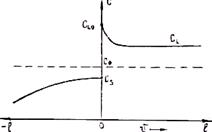
Рис. 2.22. Распределение примеси при диффузионно Рис. 2.23. Распределение концентра­ций в

контролируемой кри­сталлизации момент достижения их предель­ных значений

на фронте кристаллиза­ции

Она зависит от интенсивности движения жидкости. С увеличени­ем скорости движения жидкости, особенно при перемешивании, d быстро убывает. Если жидкость покоится, то d = Д/(v× k₀).

ГЛАВА 2.6. КОНЦЕНТРАЦИОННОЕ ПЕРЕОХЛАЖДЕНИЕ. УСЛОВИЕ УСТОЙЧИВОСТИ ПЛОСКОГО ФРОНТА КРИСТАЛЛИЗАЦИИ СПЛАВОВ

При достаточно больших скоростях кристаллизации концент­рация легирующего компонента перед фронтом кристаллизации распределена неравномерно. Распределение концентрации в рас­плаве описывает формула (2.5), из которой видно, что по мере удаления от фронта c_l более или менее быстро убывает.

Как видно из диаграммы состояния (см. рис. 2.18, а), тем­пература ликвидуса с ростом концентрации легирующего компо­нента уменьшается. Если принять линии ликвидуса и солидуса пря­мыми (рис. 2.24), то для зависимости температуры ликвидуса от концентрации компонента cl справедливо следующее уравнение:

,

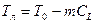где Т₀ — температура плавления металла, являющегося основой сплава; m = tg a — тангенс угла наклона прямой ликвидуса к оси концентрации компонента В.

С учетом зависимости С_L(х) получаем уравнение

,

из которого следует, что температура ликвидуса сплава перед фронтом кристаллизации по мере удаления от него увеличивает­ся, достигая при х = d значения T_л, отвечающего исходной концентрации сплава С₀. Температура ликвидуса сплава на фронте кристаллизации (С_L0 = С₀/k₀) равна T_ф = T₀ – mC₀/k₀. Схема распределения температуры ликвидуса в расплаве перед фронтом кристаллизации приведена на рис. 2.25. При охлаждении сплава в нем возникает температурный градиент через твердую фазу, равный на фронте кристаллизации GR = (dT/dx)_x=0. Примем ли­нейное распределение температуры сплава Т (х) в пределах по­граничного слоя d. При этом T(x) = T_ф + GR×x. Следует отметить, что, приняв Т (х = 0) = Т_ф, мы пренебрегаем термическим пере­охлаждениемΔT.

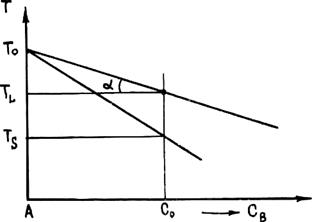
Рис. 2.24. Схема к выводу зависимости Т_л(С_L)

На рис. 2.25 линия 1 отвечает кривой изменения температуры ликвидуса, а линия 2 — распределению температуры сплава перед фронтом кристаллизации. В пределах слоя 0 £ х £ d_п температу­ра сплава ниже температуры ликвидуса, т. е. сплав является переохлажденным. Это переохлаждение обусловлено изменением состава сплава в процессе кристаллизации и называется концент­рационным переохлаждением ΔТ_к в отличие от рассмотренного в гл. 2.1 термического переохлаждения ΔT, обусловленного паде­нием температуры сплава за счет теплоотвода ниже температуры ликвидуса на фронте кристаллизации или в какой-либо части объема жидкости.

Наличие концентрационного переохлаждения создает условия для нарушения плоского характера фронта кристаллизации. На фронте кристаллизации всегда име­ются шероховатости с выступами ми­кроскопических размеров. Вершины этих выступов, находящиеся перед фронтом кристаллизации, попадают в зону кон­центрационного переохлаждения, что су­щественно повышает скорость их про­движения в глубь расплава, так как с увеличением переохлаждения любой природы линейная скорость роста кри­сталла возрастает. Поэтому скорость продвижения в глубь расплава вершин выступов больше, чем оснований, нахо­дящихся на фронте, где ΔT_к = 0 (см. рис. 2.25). В результате высота высту­пов увеличивается и плоский фронт кри­сталлизации нарушается.