Раздел 1. СТРОЕНИЕ И СВОЙСТВА ЖИДКИХ МЕТАЛЛОВ И СПЛАВОВ 1 страница

ГЛАВА 1.1. СОВРЕМЕННЫЕ ПРЕДСТАВЛЕНИЯ О ПРИРОДЕ И СТРОЕНИИ ТВЕРДЫХ И ЖИДКИХ МЕТАЛЛОВ И СПЛАВОВ

В зависимости от давления и температуры любое вещество может находиться в твердом, жидком, газообразном состояниях, а также в состоянии плазмы. Диаграмма состояния однокомпо­нентного вещества приведена на рис. 1.1. Линии АД и АД' на диаграмме разделяют

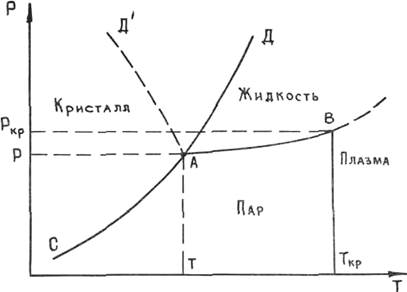
Рис. 1.1. Диаграмма состояния однокомпонентной системы

области кристаллического состояния и жид­кости. Линия АД относится к веществам, удельный объем кото­рых при плавлении увеличивается (большинство веществ), а ли­ния АД' — к воде, галлию, висмуту, сурьме, германию и крем­нию, удельный объем которых при плавлении уменьшается. Из диаграммы видно, что с увеличением давления температура плавления этих веществ уменьшается. Температура плавления большинства веществ с ростом давления увеличивается. Следует отметить, что линии АД и АД' представляют собой линии равно­весия кристалл — жидкость, т. е. геометрическое место точек, от­вечающих значениям параметров (давление Р и температура Т), при которых кристалл и жидкость находятся в динамическом равновесии друг с другом. В этом случае граница раздела твер­дой и жидкой фаз является плоской. При искривлении поверхно­сти раздела характер зависимости температуры плавления оста­ется таким же, но линии смещаются влево или вправо в зависи­мости от того, выпуклое или вогнутое твердое тело.

Температура плавления выпуклых кристаллов (сферических частиц) меньше, чем плоских, а температура плавления вогнутых кристаллов (включения металла в различных неметаллических частицах) выше, чем плоских. Связь температуры плавления кри­сталлов с их радиусом кривизны и температурой плавления плос­ких кристаллов Т_равн, которую будем называть равновесной, вы­ражается следующей формулой:

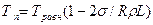, (1.1)

где а — коэффициент межфазного натяжения кристалла на грани­це с жидкостью; R — радиус кривизны кристалла и L — удельная теплота плавления. В формуле радиус кривизны выпуклого кри­сталла положительный, а вогнутого — отрицательный. Из фор­мулы видно, что для плоского кристалла (R = ∞) Т_п = Т_равн, с уменьшением радиуса кривизны температура плавления выпуклого кристалла уменьшается, а вогнутого — увеличивается.

Формула (1.1) написана для кристаллов, ограниченных сфери­ческой поверхностью. При произвольной конфигурации поверх­ности формула имеет вид

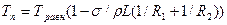, (1.2)

где R₁ и R₂ — главные (наибольший и наименьший) радиусы кривизны поверхности. Следует отметить, что изменения темпе­ратуры плавления становятся существенными лишь при радиусах поверхностей кристаллов, меньших 0,001 мм.

Линия АВ является линией равновесия жидкости и пара. Для каждого значения температуры в пределах от Т до Т_кр по ли­нии АВ мы можем найти давление насыщенного пара жидкости. Точка В отвечает критическому состоянию (точка абсолютного кипения), при котором исчезает различие между жидким и газо­образным состояниями вещества. При температуре выше Т_кр газ невозможно перевести в жидкость ни при каких давлениях. При атмосферном давлении ширина области жидкого состояния (между линиями АД и АВ) для многих металлов достаточно велика и значительно превышает применяемые в практике литья пере­гревы металла выше его температуры плавления. Например, тем­пература плавления (Т_п) алюминия — 660°С, а температура ки­пения (Т_кип) — 2327°С; для меди Т_п = 1083°С, Т_кип = 2596°С; для железа Т_п = 15Зб⁰С, T_кип = 2 880°С. Для этих металлов ис­парение в условиях литейных процессов не играет большой роли. В то же время для цинка Т_п = 419,5°С, Т_кип = 906°С; для магния Т_п = 651°С, Т_кип = 1 107°С. Для этих металлов температура ки­пения близка к температуре плавления. Они отличаются, как го­ворят, большой летучестью. Поэтому при их наличии в сплавах необходимо учитывать процессы парообразования.

При температурах, значительно превышающих Т_кр, происхо­дит ионизация газов и они переходят в состояние плазмы, пред­ставляющей собой совокупность ионов и электронов.

Как видно из диаграммы, жидкое состояние вещества зани­мает промежуточное место между твердым и газообразным состояниями. Поэтому жидкости сохраняют отдельные свойства как твердых, так и газообразных тел. Твердые тела по характеру расположения и движения атомов и молекул подразделяются на кристаллические и аморфные.

1.1.1. ПРИРОДА И СТРОЕНИЕ ТВЕРДЫХ МЕТАЛЛОВ И СПЛАВОВ

Основным свойством кристаллического состояния вещества является правильное, упорядоченное расположение атомов в про­странстве. Кристаллическое состояние вещества характеризуется четкой пространственной структурой, называемой кристаллической решеткой.

О. Браве установил, что любой кристалл можно построить на основе 14 элементарных ячеек. Наиболее распространенными ячейками металлических кристаллов являются кубическая объ­емно центрированная (ОЦК), кубическая гранецентрированная (ГЦК), компактная гексагональная (рис. 1.2). Предполагается, что в идеальном кристалле атомы расположены строго в узлах решетки и неподвижны. Кроме того, считается, что решетка яв­ляется бесконечно протяженной, т. е. каждая элементарная ячей­ка окружена достаточным количеством других ячеек (далека от поверхностей реальных тел).

Важнейшей характеристикой кристаллической решетки явля­ется координационное число, т. е. число ближайших соседей дан­ного атома. С помощью элементарных геометрических расчетов можно определить, что в объемно центрированной кубической ре­шетке координационное число — 8, т. е. около каждого атома в решетке находится 8 атомов, расположенных на минимальном расстоянии r₁ = а 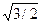, где а — параметр решетки. На расстоя­нии r₂, равном а, находится 6 атомов, и на расстоянии r₄ = а 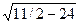атома. Расположение атомов в решетке дис­кретно, так как они находятся лишь на определенных расстояни­ях от данного атома, называемых радиусами координационных сфер. Таким образом, в объемно центрированной кубической ре­шетке на первой координационной сфере с r₁ = а 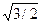, находится 8 атомов, на второй с r₂ = а — 6 атомов, на четвертой с r₄ = а 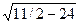и т. д. Между сферами атомов нет.

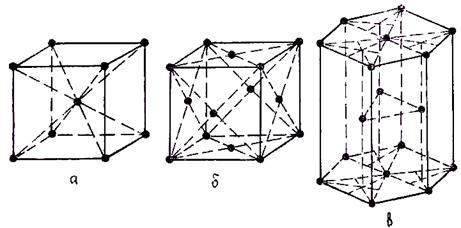
Рис. 1.2. Распространенные типы кристаллических решеток металлов и сплавов:

а — объемно центрированная; б — гранецентрированная; в — компактная гексагональная.

Для гранецентрированной кубической решетки легко устано­вить, что на первой координационной сфере с r₁ = а 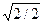на­ходится 12 атомов, на второй с r₂ = a — 6 атомов, на третьей с r₃ = а 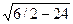атома и т. д.

Приняв в идеальном приближении, что кристалл плотно упа­кован и соседние атомы касаются друг друга, можно радиус первой сферы принять равным 2R, где R — атомный радиус. С учетом этого получаем, что для объемно центрированного куба r₁ = 2R, r₂ = 4R 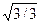, r₄ = 2R 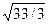, а для гранецентрированного куба r₁ = 2R, r₂ = 2R 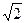, r₃ = 2R 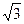и r₄ = 4R.

С учетом полученных значений радиусов координационных сфер и числа находящихся на них атомов можно построить гра­фики пространственного расположения атомов в объемно цент­рированной и гранецентрированной кубических решетках (рис. 1.3).

Такова в общих чертах характеристика идеального кристал­ла. Реальный кристалл имеет целый ряд существенных особенно­стей. Прежде всего, атомы не находятся неподвижно в узлах ре­шетки, а их атомные диаметры не совпадают с радиусом первой координационной сферы.

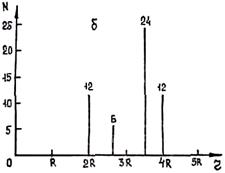
Рис. 1.3. Распределение числа атомов по первым координационным сферам для

объемно центрированного (а) и гранецентрированного (б) куба.

Известно, что атомы совершают колеба­ния относительно узлов решет­ки, которые являются положе­ниями равновесия. Интенсив­ность колебаний, или теплово­го движения атомов, увеличи­вается с ростом температуры. При низких температурах ато­мы совершают колебания от­носительно фиксированных уз­лов, т. е. так называемое транс­ляционное движение отсутству­ет и атомы не перемещаются по­ступательно по решетке. Од­нако с увеличением темпера­туры вероятность появления трансляционного поступатель­ного движения атомов увели­чивается. Для того чтобы оха­рактеризовать механику реаль­ного кристалла, рассмотрим вопрос о межчастичном взаи­модействии в кристаллах.

Как известно, атомы метал­лов, как и других элементов, представляют собой положи­тельные ядра с вращающими­ся относительно них электро­нами, обладающими разными энергиями (находящимися на разных энергетических уровнях). При сближении любых двух атомов, начиная с некоторого расстояния, их электронные оболочки перекрываются (речь идет о внешних оболочках), подобно тому как при образовании молеку­лы водорода электроны каждого атома попадают в сферу влияния ядер обоих атомов и обобществляются, т. е. процесс сближения атомов металла приводит к обобществлению части их электронов. В пределах кристаллической решетки эти электроны уже не при­надлежат только своим атомам. В результате образуется система, в которой в узлах решетки находятся положительно заряженные ионные остовы, а в объеме решетки расположены свободные коллективизированные электроны. Именно наличием этих электронов объясняется высокая электропроводность металлов.

Рассмотрим процесс сближения атомов. Если расстояние меж­ду ними достаточно велико, то атомы можно представить как два диполя, которые притягиваются друг к другу. При этом заряды ближайших атомов обоих диполей вследствие электростатической индукции имеют разную полярность. Это явление, как известно из физики, называется поляризацией. Силы притяжения, возни­кающие вследствие поляризации, обратно пропорциональны рас­стоянию между атомами в седьмой степени (F_пр ~ 1/R⁷). Эти силы называются силами Ван-дер-Ваальса. Такая зависимость сил притяжения говорит о том, что они при увеличении расстоя­ния между атомами быстро убывают (на расстоянии, в несколько раз превышающем размеры атомов, эти силы практически исче­зают).

Если атомы сблизить на расстояние, сравнимое с размерами электронных орбит, например несколько меньшее диаметра этих орбит, то электронные оболочки начинают деформироваться и между атомами возникают силы отталкивания, называемые об­менными силами. Силы отталкивания близкодействующие, они убывают с увеличением расстояния быстрее, чем силы притяже­ния. Известно эмпирическое приближение, что F_от ~ 1/R¹³. Про­стейшей и широко применяемой формулой для описания потенци­ала межчастичных взаимодействий является потенциал Ленарда — Джонса:

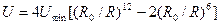, (1.3)

где R₀ — расстояние, отвечающее минимуму потенциала; U_min — модуль минимума потенциала.

Формула Ленарда — Джонса моделирует изменение потенциа­ла взаимодействия двух частиц. Рассмотрим две частицы, при­чем левую закрепим неподвижно. Изменение потенциала при из­менении расстояния на dR равно работе сил взаимодействия, т. е.

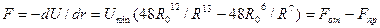, (1.4)

где 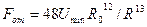и

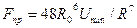
Графически изменение результирующей силы взаимодействия и энергии связи частиц с изменением расстояния показано' на рис. 1.4. Видно, что при R = R₀ F = 0, т. е. |F_пр| = |F_от|. Положе­нию равновесия отвечает минимум энергии связи, т. е. потенци­альная яма. Если бы не было теплового движения атомов, то! атомы в кристаллической решетке располагались бы на расстоя­нии Ro друг от друга, которое физически определяет параметр решетки.

Отмеченные выше закономерности имеют общий характер. В чем же специфика металлов? Обменные силы отталкивания зависят от степени заполнения внешней электронной оболочки. С ее увеличением силы отталкивания возрастают. Как известно, наибольшую заполненность внешней оболочки имеют инертные газы (гелий, аргон, криптон и т. д.). На внешних оболочках у них максимально возможное число электронов — 8. При сближении атомов оболочки практически не перекрываются и не происхо­дит образование обоб­щенных электронов и ионов. Поэтому инерт­ные газы — диэлект­рики.

Рассмотрим случай, когда внешние элект­ронные оболочки не за­полнены электронами (число внешних элект­ронов меньше 8). Здесь возможно большее сближение атомов и перекрытие электрон­ных оболочек с образо­ванием ионов и коллек­тивизированных элек­тронов. Свободные электроны оказывают влияние на силы притяжения. Электроны, находящиеся между двумя положитель­ными ионами, притягивают их с силой, большей силы притяжения ионов, так как расстояние между каждым ионом и электронами меньше, чем расстояние между ионами. При этом всякое измене­ние параметра решетки вызывает изменение плотности электронов между ионами, что, в свою очередь, приводит к возникновению сил, стремящихся вернуть решетку в исходное состояние. Такой тип связи называется металлическим. Силы отталкивания теперь связаны с деформацией внутренней заполненной электронной оболочки иона, имеющей радиус R₂ < R₁, где R₁ — радиус внеш­ней оболочки, электроны которой коллективизированы. Равно­весие ионов достигается на расстоянии R₀, находящемся в интер­вале 2R₁ — 2R₂.

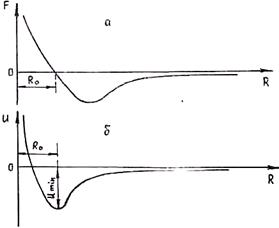
Рис. 1.4. Зависимость силы (а) и потенциала взаимодействия (б) двух атомов от расстояния между ними.

Металлические чистые кристаллы очень устойчивы по отно­шению к сильным смещениям частиц. Если металл растянуть, то увеличится вероятность нахождения электронов между ионами (электронная плотность) и появятся силы, стремящиеся вернуть решетку в исходное состояние. Если металл сжать, то электроны вытесняются из межионного пространства, электронная плотность падает и силы отталкивания начинают превышать силы притяже­ния. При снятии внешнего воздействия решетка вернется в ис­ходное состояние. Поэтому чистые металлы способны без разрушения выдерживать большие пластические деформации. Хрупкость отдельных металлов и сплавов объясняется наличием в решетке различных кристаллических дефектов (вакансии, дислокации и т. п.).

Электроны оказывают существенное влияние на свойства ме­таллов. Однако более детальное рассмотрение электронной теории металлов выходит за рамки данного курса. Интересующимся можно рекомендовать книгу Н. Б. Брандта, С. М. Чудинова «Элек­тронная структура металлов» (М.: Изд-во Моск. ун-та, 1973. 332 с.).

До сих пор мы рассматривали кристалл в условиях, когда кинетическая энергия частиц равна нулю, т. е. частицы непод­вижно находятся в положениях равновесия (параметр решетки равен R₀) • Однако это невозможно даже при абсолютном нуле. Как и в любом теле, частицы в твердом металле обладают кине­тической энергией Е, которая связана с температурой. В первом приближении можно принять, что E = kT, т. е. с ростом темпера­туры Е увеличивается. Если под действием теплового движения положение равновесия нарушится и расстояние между частица­ми увеличится, то силы притяжения превзойдут силы отталкива­ния и появится сила, возвращающая частицы в положение равно­весия. При уменьшении расстояния между частицами силы от­талкивания превзойдут силы притяжения и возвращающая сила снова будет направлена к положению равновесия. Таким обра­зом, возникает ситуация, характерная для колебательного дви­жения. Однако колебания частиц в данном случае будут ангар­моническими.

Для возникновения гармонических колебаний необходимо, что бы возвращающая сила была пропорциональна отклонению от положения равновесия. В этом случае кривая энергии связи сим­метрична (рис. 1.5). Пусть при температуре Т₁ энергия теплового движения Е₁, а при температуре Т₂ > Т₁ энергия теплового дви­жения Е₂ > Е₁. Видно, что частица совершает симметричные коле­бания, причем с ростом температуры амплитуда колебаний уве­личивается. Положение же равновесия при этом не изменяется.

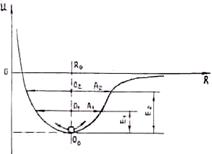
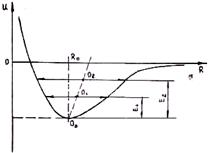
Рис. 1.5. Зависимость потенциала взаимодей- Рис. 1.6. Изменение параметра кристаллической

ствия частиц от расстояния между ними при решётки при нагревании

гармоническом ха­рактере колебаний

В кристаллах же возвращающая сила, как видно из форму­лы (1.4), не пропорциональна отклонению от положения равно­весия (R — в знаменателе). С ростом расстояния силы отталки­вания убывают быстрее, чем силы притяжения. Поэтому кривая энергии связи несимметрична (рис. 1.6). С увеличением темпера­туры, а следовательно, и энергии теплового движения возрастает амплитуда колебаний, но положение равновесия смещается в сторону увеличения расстояния между частицами. Это приводит к увеличению параметра решетки, т. е. к тепловому расширению. Таким образом, термическое расширение тел объясняется не рос­том амплитуды тепловых колебаний частиц, а ангармоническим характером этих колебаний.

Мы рассмотрели характер движения частиц в упрощенном случае двухчастичного линейного кристалла. В действительности в пространственной решетке колебания носят сложный характер. Каждая частица испытывает действие сил связи со стороны всех окружающих ее частиц кристалла. Так как силы связи быстро убывают с увеличением расстояния, то учитывают действие толь­ко ближайших «соседей». Если изменить характер движения ка­кой-либо одной частицы, то это изменение будет передано сосед­ним частицам, а от них — к их «соседям» и т. д. Например, если тело с одной стороны нагреть, то колебания частиц в этой части кристалла усилятся. Это усиление теплового движения через силы связи передастся соседним частицам и достигнет противополож­ного конца тела, т. е. повышение температуры в какой-либо части тела приведет к ее повышению в остальных. Такова природа теплопроводности.

Следует отметить, что при этом не происходит направленного перемещения частиц. Они колеблются около своих положений равновесия. В кристалле разные частицы колеблются с разными частотами и в разных фазах. Период колебаний частиц имеет по­рядок 10^-13 с. Таким образом, если мы «сфотографируем» части­цы в кристалле с временем экспозиции, меньшим 10^-13 с, то ни­какого порядка в расположении частиц не увидим, так как все они будут находиться на разных расстояниях от положений равно­весия. Реально же время экспозиции всегда больше 10^-13 с. По­этому фактически мы увидим частицы в положениях равновесия, т. е. упорядоченную структуру кристалла.

В кристалле энергия теплового движения меньше энергии свя­зи, т. е. E < |U_min|. С увеличением температуры растет энергия теплового движения, и при некоторой температуре она прибли­зится к энергии связи. При этом произойдет плавление кристалла» т. е. переход в жидкое состояние. Для иллюстрации поведения частиц в кристалле при нагревании рассмотрим изменение энер­гии связи двух частиц в зависи­мости от положения между ними средней частицы. Если расстоя­ние между частицами достаточно мало (температура значительно меньше температуры плавления), то энергия средней частицы рас­пределена в соответствии с рис. 1.7, а. При этом средняя частица имеет минимум энергии посредине между крайними ча­стицами, что отвечает правильно­му расположению частиц в кри­сталле. Если же крайние частицы раздвинуть на очень большое расстояние, что соответствует ис­парению металла, то средним по­ложениям частицы будет соответ­ствовать отсутствие сил взаимо­действия. Кривая энергии средней частицы при этом показана на рис. 1.7,б. Видно, что на значи­тельных расстояниях между ча­стицами средняя частица не будет испытывать взаимодействия с крайними, как в идеальном газе.

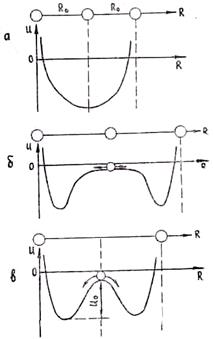
Рис. 1.7. Изменение потенциала сред­ней частицы при малых (а), очень больших (б) и некоторых средних (в) расстояниях между крайними ато­мами

Рассмотрим случай, когда тем­пература близка к температуре плавления. Крайние частицы находятся на таком расстоянии друг от друга, что энергия связи средней частицы будет изменяться в зависимости от расстояния, как показано на рис. 1.7, в. Поло­жение в центре промежутка между крайними частицами будет неустойчивым и частица перейдет в потенциальную яму около левой или правой частицы. При этом кристалл разрушится. Нару­шится дальний порядок в размещении частиц. Частицы первой координационной сферы (ближайшие к данной частице) останут­ся связанными с этой частицей, а более удаленные потеряют с ней связь. Говорят, что сохранился ближний порядок в размещении атомов. Средняя частица при этом совершает колебания только около одной из указанных на рисунке частиц. Следует, однако, отметить, что данное положение будет динамическим. Глубина потенциальной ямы не столь велика, чтобы средний атом, нако­пив вследствие флуктуации энергию, не перешел в потенциальную яму около соседней, т. е. правой, частицы. При этом происходит смена положения равновесия колебаний. Описанная картина от­вечает жидкому состоянию.

Таким образом, частицы в жидкостях совершают колебания такого же типа, что и в кристаллах, но положения равновесия, относительно которых совершаются колебания, не остаются не­подвижными. Совершив некоторое число колебаний около дан­ного положения равновесия, частица скачком переходит в новое положение и продолжает там колебаться, пока снова не перескочит в новое положение. По Я. И. Френкелю, длительность пре­бывания частицы около данного положения равновесия — время оседлой жизни — определяется по формуле т^т-ое^⁰^⁷', где t₀ — период колебания около положения равновесия; U₀ — высота по­тенциального барьера, отделяющего два положения равновесия (глубина потенциальной ямы); k — постоянная Больцмана; Т — абсолютная температура. Обычно t имеет порядок 10^-10 с. Пе­риод же колебаний то имеет порядок 10^-12 — 10^-13 с. Значит, ча­стица, прежде чем переменить место, совершит 100 — 1000 коле­баний.

Молекулы жидкости в основном ведут оседлый образ жизни, что сближает их с молекулами твердых тел. С увеличением тем­пературы время оседлой жизни уменьшается, т. е. снижается доля колебательного движения и увеличивается доля поступательного трансляционного движения. Таким образом, в жидкостях сохра­няется на достаточно высоком уровне взаимодействие между ча­стицами, сосуществующее с тепловым движением. Такое состояние в отличие от газов, где энергия взаимодействия значительно меньше энергии теплового движения, называется конденсирован­ным состоянием. Отличие жидкости от твердых кристаллических тел состоит в наличии кроме колебательного движения трансля­ционного движения, доля которого увеличивается с повышением температуры. Однако для более полного понимания процесса плавления необходимо отметить, что и в твердых телах частицы могут иметь трансляционное движение, усиливающееся по мере приближения к температуре плавления.

Как известно из молекулярно-кинетической теории, среди ча­стиц газа или жидкости, находящихся при данной температуре, можно найти частицы, обладающие разной кинетической энерги­ей, в том числе и значительно отличающейся от соответствующего данной температуре среднего значения E = kT.

Однако кривая распределения числа частиц по энергиям име­ет острый максимум при E = kT, т. е. относительное количество частиц, обладающих энергией, сильно отличающейся от E = kT, невелико. Например, количество частиц, имеющих энергию, в 2 раза большую этой величины, составляет всего 5%. Таким об­разом, в жидкости при данной температуре имеется определен­ное количество частиц, обладающих кинетической энергией, пре­вышающей энергию

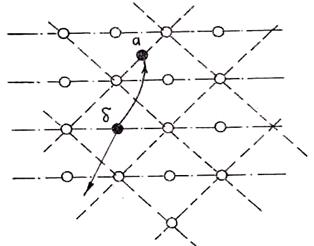
Рис. 1.8. Схема образования вакансий и дислоци­рованных атомов

связи частиц в кристалле. Вспомним, что именно наличием этих быстрых частиц в физике объясняют процесс испарения. Такая быстрая частица в кристалле преодо­леет силы связи с «соседями» и покинет данную ячейку, пере­местившись в соседнюю. Там она займет место в узле, если оно свободно, или разместится в объеме узла (в междоузлии). Место этой частицы в прежней ячейке окажется вакантным. Говорят, что там образовалась вакансия (или дырка). Переместившийся атом, если он находится в междоузлии, называется дислоциро­ванным. Схема образования дислоцированных атомов и вакан­сий показана на рис. 1.8.

Наличие вакансий в твердом теле создает условия для транс­ляционного поступательного движения частиц. Процесс переме­щения частиц и вакансий в чистом металле называется самодиф­фузией. Для оценки числа вакансий Я. И. Френкелем предложена следующая формула: Nв=Ne-^u/^kт, где N_в — число вакансий; N — общее число частиц; U — энергия образования вакансии, близкая к энергии испарения. Я. И. Френкелем выполнен следующий расчет для кадмия. При комнатной температуре (300 К) вакансий мало, N_в/N = 10^-18. Уже при температуре 600 К N_в/N = 10^-9. Осо­бенно быстро растет количество вакансий вблизи температуры ллавления (до 1,5 %).

Вакансии и дислоцированные атомы относятся к точечным дефектам кристаллической решетки, приводящим к ее искажению и созданию около дефектов напряженного состояния. Характер искажения решетки в плоском изображении показан на рис. 1.9.

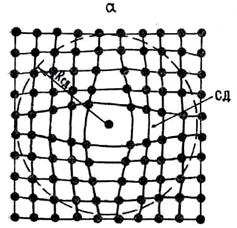
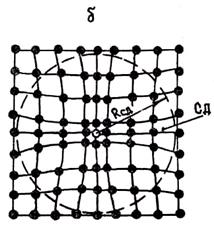
Рис. 1.9. Схема искажения кристаллической решетки около дислоцированного атома (а) и вакансии (б)

Установлено, что геометрия ионного остова и электрический потенциал решетки при этом искажаются на значительном рас­стоянии, равном 10 — 20 межатомным расстояниям от дефекта. Эту деформированную зону называют сферой деформации (СД). Сфе­ра деформации около вакансии несет отрицательный заряд, так как положительный ион замещен вакансией (дыркой). Однако электрическое взаимодействие вакансий на расстояниях, превы­шающих радиус сферы деформации R_сд, весьма мало. Так как вакансии перемещаются по кристаллу, то перемещаются и сферы деформации. При сближении СД на расстояния l £ R_сд между ними возникают силы отталкивания.

1.1.2. СОВРЕМЕННЫЕ ПРЕДСТАВЛЕНИЯ О МЕХАНИЗМЕ ПЛАВЛЕНИЯ

В объяснении процесса плавления главную роль из рассмот­ренных дефектов решетки играют вакансии. На их роль впервые обратил внимание Я. И. Френкель. В литературе имеется целый ряд теорий, объясняющих плавление. На наш взгляд, очень убедительной выглядит вакансионно-кластерная теория И. В. Гаврилина и Г. С. Ершова.

При низких температурах в кристалле число вакансий не­велико и расстояния между сферами деформации больше их диа­метров. Поэтому СД не взаимодействуют друг с другом и подоб­но газовым частицам свободно, хаотически перемещаются по кри­сталлу (рис. 1.10, а). При некото­рой температуре Т = Т_к концент­рация вакансий возрастает до ве­личины, при которой расстояния между СД сравниваются с их диаметрами. При этом СД смыка­ются, образуя плотную упаковку (рис. 1.10,6). Дальнейшее повы­шение температуры должно со­провождаться увеличением числа вакансий. Однако при T = T_к вследствие взаимного отталкива­ния СД места для размещения новых вакансий отсутствуют. Воз­никает противоречие между тен­денцией сохранения дальнего по­рядка и тенденцией к росту числа вакансий.