Определенный интеграл. Пусть функция определена на отрезке

Пусть функция 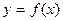определена на отрезке 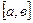. Разобьём этот отрезок на части точками 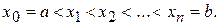Получим 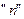частичных отрезков длиной 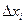= 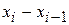каждый.

В каждом частичном отрезке выберем произвольную точку 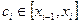и вычислим в ней значение функции .

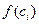Составим сумму произведений:

.

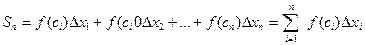Эта сумма называется интегральной суммой функции 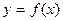на отрезке 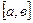. Перейдем к пределу в последнем выражении, когда максимальный из отрезков .

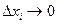Если при этом сумма 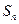имеет предел 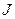, не зависящей от способа разбиения отрезка 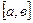на части и от выбора точек 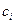в них, то число 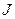называют определенным интегралом от функции 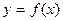на отрезке :

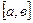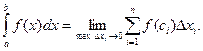
В таких случаях функцию 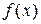называют интегрируемой на отрезке 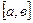и для нее справедлива теорема, утверждающая, что любая непрерывная на отрезке 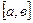функция, является интегрируемой.