Геометрические характеристики сечения.

Рассмотрим произвольное поперечное сечение. Оно характеризуется рядом параметров, которые используются в инженерных расчетах:

A - площадь поперечного сечения,

I_z, I_y - моменты инерции относительно осей х и у (осевые моменты инерции),

I_zy - центробежный момент инерции.

Из курса сопротивления материалов известно, что жесткость стержня при растяжении (сжатии) зависит от площади поперечного сечения A, а при изгибе – от величины осевого момента инерции I_z.

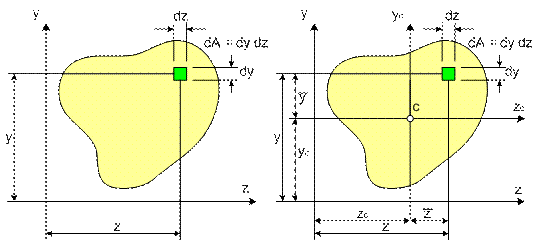
Рис. 3.2

По определению все перечисленные выше величины представляют собой интегралы, вычисленные по площади:

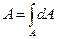- площадь, (3.1)

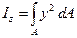- момент инерции относительно оси z, (3.2)

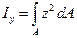- момент инерции относительно оси у, (3.3)

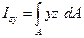- центробежный момент инерции. (3.4)

В формулах (3.1) – (3.4) dA - представляет собой площадь бесконечно малой части сечения, а z и y – его координаты (см рис. 3.2).

Перечисленные интегралы могут быть вычислены в любой системе координат, однако следует заметить, что для использования в расчетах необходимы моменты инерции относительно центральных осей,то есть осей, проходящих через центр тяжести сечения.

Известно, что координаты точки, в которой находится центр тяжести сечения, следует определять (см. курс сопротивления материалов) по формулам:

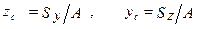, (3.5)

де S_y и S_z - соответственно статические моменты относительно осей y и z, которые также как и моменты инерции являются интегралами:

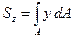- статический момент относительно оси х, (3.6)

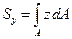- статический момент относительно оси у. (3.7)

При переходе к системе центральных осей y_cz_c координаты элементарной части площади dA изменятся (см. рис. 3.2) следующим образом:

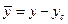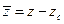, (3.8)

и тогда вычисление интегралов в формулах (3.2) – (3.4) необходимо будет производить по формулам:

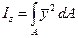(3.9)

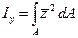(3.10)

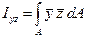(3.11)

Представим примерную схему алгоритма для вычисления основных геометрических характеристик сечения, имеющего произвольную форму.

Накроем поперечное сечение прямоугольной сеткой, имеющей ячейки очень малого размера, как это показано на рис. 3.3, и введем булевскую (логическую) матрицу 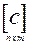, элементами которой будут являться нули, если ячейка находится вне контура сечения, и единицы, если внутри контура.

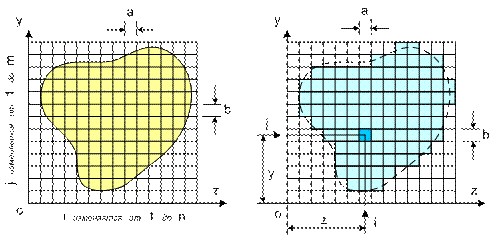
Рис. 3.2

В случае использования процедур графического ввода информации с монитора, в качестве ячеек такой сетки могут служить пиксели экрана.

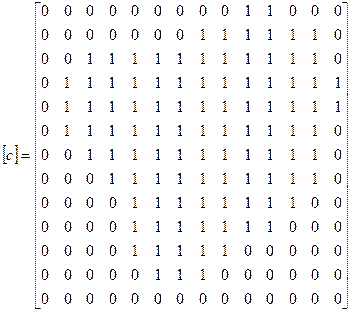
Входной информацией будут: m, n, a, b и матрица [c], а выходной информацией – геометрические характеристики, вычисленные относительно центральных осей, и его координаты.

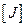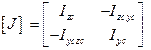Вычисленные моменты инерции являются компонентами симметричного тензора II ранга и могут быть представлены в виде матрицы. Чтобы не путать полученную матрицу с единичной, обозначим ее :.

, где 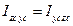(3.12)

Предположим, что некоторый вектор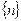

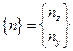. (3.13)

является собственным вектором матрицы 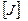, то есть существует некоторое число 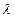, для которого справедливо равенство

.

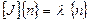Умножив правую часть этого равенства на единичную матрицу, преобразуем его к виду

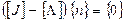(3.14)

где 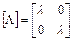- квадратная диагональная матрица.

Соотношение (3.14) представляет собой однородную систему двух уравнений

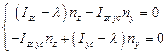(3.15)

которая имеет ненулевое решение только при обращении в ноль определителя матрицы системы, то есть при

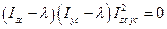. (3.16)

Выражение (3.16) представляет собой квадратное уравнение, которое при записи его в канонической форме имеет вид:

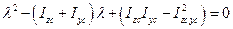(3.17)

Решая это уравнение, получим два корня, представляющие собой собственные числа матрицы (3.12):

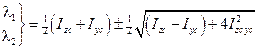, (3.18)

которые в курсе сопротивления материалов называют главными центральными моментами инерции и обозначают

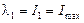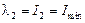, (3.19)

Поочередно подставим полученные значения главных моментов инерции в уравнения системы (15) и, решая ее, получим собственные вектора матрицы (3.12). Каждый из найденных собственных векторов определит положение одной из главных центральных осей поперечного сечения, то есть осей, относительно которых вычислены главные центральные моменты инерци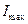и и 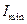. В системе главных центральных осей центробежные моменты 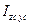обращаются в ноль и матрица (3.12) преобразуется к диагональному виду

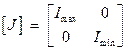(3.20)