Специальные виды матриц

Перестановочные матрицы.

Возьмем единичную матрицу 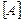= 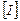и модифицируем ее следующим способом:

- выделим в ней i – й столбец и i – ю строку, j - й столбец и j– ю строку

(i ≠ j);

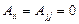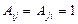- положим и (рис. 2.4).

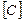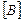
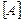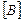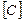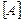
Легко убедиться, что в этом случае умножение вида = приводит к перестановке в исходной матрице i-го и j-го столбцов. В то же время, умножение вида = 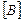приводит к перестановке в исходной матрице 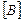i-й и j-й строк. Матрица , используемая для осуществления такой операции, называется перестановочной.

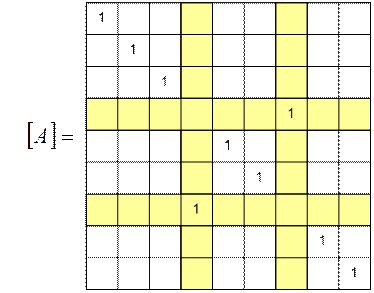
Рис. 2.4

Матрицы преобразования системы координат (матрицы поворота осей).

Если для некоторого вектора 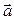(рис. 2.5 ) компоненты, заданные в одной системе координат матрицей-столбцом 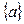надо вычислить в другой, полученной путем поворота, системе координат, представив столбцом 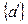, то указанное преобразование можно выполнить с помощью операции

.

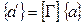Известно, что компоненты некоторого двумерного вектора 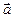изменяются при повороте системы координат на угол 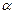по следующему правилу (рис.2.5):

,

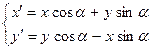Следовательно, в этом случае матрица 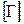должна быть сформирована следующим образом

.

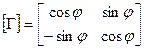Очевидно, что определитель матрицы 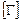равняется единице, поскольку

,

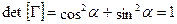Легко также убедиться в том, что в случае ортогональных осей матрица преобразования системы координат обладает свойством 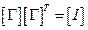. По определению обратной матрицы 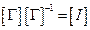. Поэтому должно иметь место равенство

.

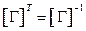Матрицы, для которых обратная матрица равна транспонированной матрице, называются ортогональными.

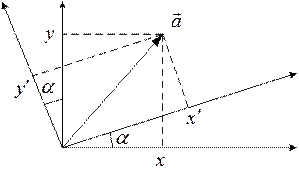
Рис. 2.5