В матрице указаны веса ребер связного неориентированного четырехвершинного графа. Найдите вес минимального остовного дерева.
¥ 5 7 6
Yen; 2 4
Yen; 3
Yen;
B)10
Найдите цикломатическое число графа, заданного множеством вершин X={1, 2, 3, 4, 5} и отношением на этом множестве: 5≤| x+y | ≤8.
C)3
Пусть Х - множество, |X|=6. Сколькими способами можно разбить это множество на 3 подмножества таких, что первое из них содержит 3 элемента, второе - 2 элемента, третье - 1 элемент?
D)60
Какой граф называется неориентированным?
C)граф, содержащий только ребра
Какое из перечисленных множеств не является счетным?
A)множество всех иррациональных чисел
Из 37 студентов, изучающих иностранные языки, немецким языком владеют 15 человек, английским- 15 человек, французским-14. Английским и французским владеют 4 человека, немецким и французским - 2 человека, немецким и английским-2 человека. Сколько человек владеют всеми тремя языками?
E)1
Логическая функция f(x,y) задана своими значениями на последовательности наборов значений аргументов (0,0), (0,1), (1,0), (1,1):
f = ( 0 1 1 1 ). Найдите ее совершенную конъюнктивную нормальную форму (СКНФ).
E)(x V y)
Укажите, какие из трех заданных формул эквивалентны:
1) 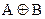 2) (
2) ( 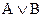 )
) 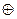 (
( 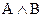 )
)  3)
3) 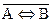
D) 1, 2, 3
Какая из приведенных систем логических функций не является функционально полной?
E) {x &y, x V y }
Совершенная дизъюнктивная нормальная форма (СДНФ) логической функции f(x,y)= x | y имеет вид
A) 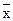 &
& 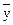 V
V 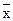 &y V x&
&y V x& 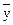
Сколько можно построить бинарных отношений на множестве мощности 3?
B)512
Найдите цикломатическое число графа, заданного множеством вершин X={1,2,3,4,5} и отношением на этом множестве G: |x-y|>=3.
C)0
Сколькими способами можно разбить множество из 5 объектов на 3 непустые части?
C)25
Какой граф является однохроматическим?
B) нуль - граф
Полином Жегалкина для функции f(x, y) = x V y имеет вид
B)x 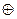 y
y 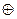 xy
xy
Дата добавления: 2014-12-06; просмотров: 1739;
