Постройте логическую формулу от трех переменных, которая истинна в том и только том случае, когда ровно две переменные ложны.
E) 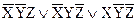
Найдите область истинности предиката х + 2 < 3х − 4
С) (3; +∞)
Какое из предложений не является высказыванием?
E) A >0
Какие из следующих высказываний истинны (и), а какие – ложны (л) (переменные принимают значения из R- множества вещественных чисел)?
1) "x ( |x| 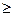 0) 2) $y
0) 2) $y 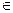 R (y2+y+1=0) 3) $x ( x3 < x2 )
R (y2+y+1=0) 3) $x ( x3 < x2 )
D)1) и 2) л 3) и
Пусть А(х), В(х) – любые предикаты. Какие из следующих четырех формул эквивалентны формуле А(х) → 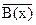 ?
?
1) А(х) 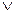 В(х) 2)
В(х) 2) 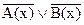 3) В(х)→
3) В(х)→ 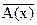 4)
4) 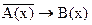
B) 2, 3
Сколькими способами можно раскрасить квадрат, разделенный на 4 части, если имеется 6 различных красок и не допускается раскрашивание разных частей в один цвет?
C)360
Найдите хроматическое число графа, заданного множеством вершин X={0,1,2,3,4,5} и отношением на этом множестве G: |x-y|>=2.
A) 4
Какой граф является однохроматическим?
C)нуль - граф
Найдите хроматическое число графа, заданного множеством вершин X={1, 2, 3, 4, 5, 6} и отношением на этом множестве : | x-y | >=3.
B)3
Найдите диаметр графа, заданного множеством вершин X={1, 2, 3, 4, 5, 6} и отношением на этом множестве : | x-y | >=3.
D)3
Найдите диаметр графа, заданного множеством вершин X={0,1,2,3,4,5} и отношением на этом множестве G: |x-y|>=2.
E)2
Какой граф называется деревом?
C) связный граф без циклов
Пусть Х и Y - два множества, |X|=3, |Y|=5. Сколько существует инъективных отображений X®Y?
E)60
Пусть Х и Y - два множества, |X|=3, |Y|=5. Сколько существует функциональных отображений X®Y ?
B) 125
На множестве А= {1, 2, 3, 4} задано бинарное отношение {(1,3), (1,4), (3, 1), (4, 1), (2,3)}. Является ли оно 1)рефлексивным, 2)антирефлексивным, 3)симметричным, 4)антисимметричным, 5)транзитивным?
A)1) нет 2) да 3) нет 4) нет 5) нет
Функции f(x1, …,xn) и g(x1,…,xn) называются двойственными друг другу, если для всех наборов значений переменных выполняется равенство
D)f(x1, …, xn) = 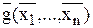
Дата добавления: 2014-12-06; просмотров: 2460;
