Идеализация с помощью конечных элементов

При построении математической модели геометрия конструкции представляется набором конечных элементов очень простой формы. Изменение перемещений и напряжений внутри одного элемента моделируется также очень простыми функциями, линейными или квадратичными. При рассмотрении соединений конечных элементов действующие между ними напряжения представляются эквивалентными сосредоточенными силами (и иногда моментами), приложенными в точках соединения – узловых точках. Соответственно смещения этих точек – степени свободы используются для описания перемещений элемента. К узловым силам приводятся также внешние распределенные нагрузки, действующие на поверхности тела. Закрепление границ тела также сводится к закреплению узловых точек. Таким образом, расчетная модель становится дискретной.

Реальное поведение конструкции схематично показано на рис. 4.2 a, а ее конечно-элементная модель – на рис. 4.2 b. Идеализация конструкции должна выполняться таким способом, чтобы при уменьшении размеров элементов поведение модели стремилось к поведению реальной конструкции.

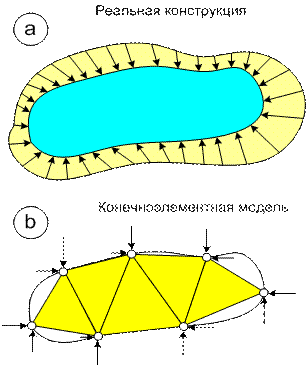
Рис. 4.2

Следует сразу заметить, что существует очень широко используемый подход, основанный на энергетических или вариационных принципах, при котором основополагающие концепции метода рассматриваются несколько иначе.

При замене реальной конструкции ее упрощенной моделью могут возникать ошибки. Посмотрим, какой характер они имеют.

При решении плоских или пространственных задач, поскольку уравнения равновесия и неразрывность деформаций выполняется лишь локально – в узлах, возможны нарушения непрерывности деформаций или поля напряжений на границах между элементами.

Например, на рис. 4.3 показано, что если перемещения в пределах элемента изменяются по линейному закону, то при равенстве перемещений в узлах соблюдается непрерывность поля перемещений вдоль всей линии стыка. Но если для перемещений внутри элемента использовать квадратичную функцию, то при равенстве перемещений в узлах вдоль сторон элементов меду ними могут возникать зазоры. Естественно, что величина этих зазоров уменьшается при уменьшении размеров элементов. Похожая картина возникает при рассмотрении напряжений действующих вдоль сторон элементов.

Таким образом, при расчете методом конечного элемента основные ошибки возникают в результате локальных нарушений непрерывности поля перемещений (нарушение неразрывности деформаций) и поля напряжений (уравнений равновесия).

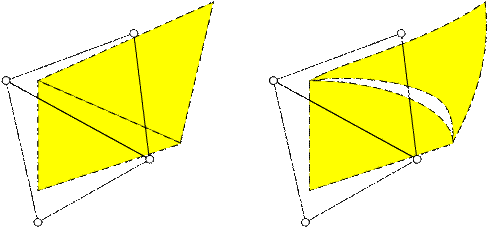
Рис. 4.3

Такая проблема не возникает при рассмотрении стержневых конструкций, поскольку элементы в них соприкасаются и взаимодействуют только в узловых точках. Поэтому, если для каждого из узлов выполнены уравнения равновесия и в узловых точках обеспечена неразрывность деформаций стержней, то такое решение можно считать точным.

Другим источником возникновения ошибок является накопление погрешности при решении системы уравнений, которое для систем алгебраических уравнений большой размерности может быть весьма значительным. Снижение этих ошибок, имеющих чисто вычислительный характер, является самостоятельным предметом для исследований.