Программы общего назначения

Основные соотношения метода конечных элементов и его процедуры, такие как построение сетки конечных элементов, учет условий на границах области или решение системы алгебраических уравнений мало зависят от физического содержания решаемой задачи. Это привело к повсеместному созданию программных средств, объединяющих решение разнотипных физических задач в рамках одного пакета программ. Например, такая программа, как ANSYS, возникшая как программа для определения напряженно-деформированного состояния конструкций, в настоящее время представляет собой огромный комплекс, позволяющий моделировать самые разнообразные физические процессы в сплошных средах и учитывать взаимодействие этих процессов.

Представленные на рис. 4.4 четыре составные части присутствуют практически во всех программах общего назначения. Опишем их содержание.

На первом этапе осуществляется ввод информации о геометрии конструкции, данных о том, каким образом закреплены ее границы, о действующих на нее внешних силах. Указываются материалы, из которых конструкция изготовлена. Осуществляется подробный контроль за непротиворечивостью введенной информации и ее графическое отображение.

На втором этапе выполняется разбивка сетки конечных элементов, привязка внешних воздействий к узлам сетки. Большое значение имеет часть, названная библиотекой конечных элементов. Здесь хранится информация о различных типах конечных элементов. На этапе выполнения осуществляется выборка из библиотеки соответствующих процедур и построение с их помощью алгебраических соотношений для каждого конечного элемента.

В библиотеке физических моделей в закодированной форме хранятся физические соотношения, используемые при расчете конструкций из упругих материалов (закон Гука), модели, позволяющие учитывать пластические деформации и деформации ползучести. Могут храниться уравнения теплопередачи или гидродинамики и т.д.

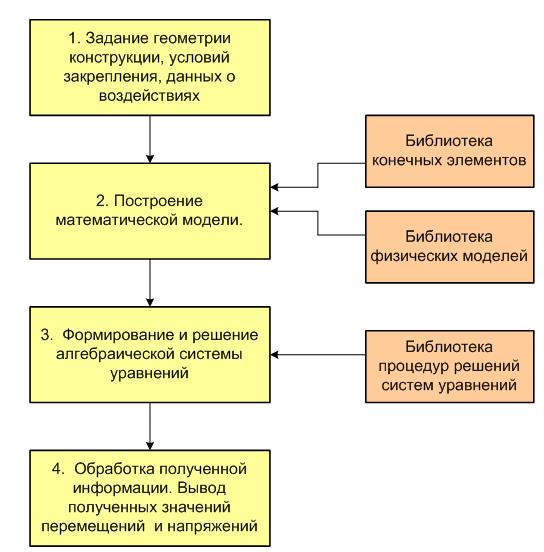
Рис. 4.4

Обе библиотеки должны иметь возможность непрерывно пополняться новыми моделями конечных элементов и физических зависимостей.

На третьем этапе осуществляется сборка конечных элементов в единое целое. Для статических задач это означает формирование, и затем решение системы линейных алгебраических уравнений с известной правой часть. В зависимости от структуры и размера построенной математической модели решение системы уравнений может осуществляться различными методами. Для небольших задач более эффективны прямые методы, представляющие собой модификации метода Гаусса. Для задач большой размерности более эффективными становятся итерационные методы последовательных приближений. Решение задач колебания и устойчивости может потребовать решения задачи определения собственных значений и собственных векторов. Процедуры для формирования и решения систем алгебраических уравнений хранятся в библиотеке процедур решения систем уравнений.

На последнем этапе исследователю в текстовом или графическом формате выдается решение, которое помогает ему правильно определить пропорции конструкции и разрешить другие вопросы проектирования. При решении задач расчета конструкций такой информацией являются данные о перемещениях точек конструкции и о действующих внутри нее напряжениях.