Принятая система координат. Узловые силы и перемещения

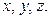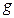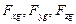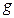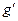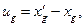
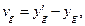
Обычно будем использовать декартовую систему координат, оси которой на рис. 5.1 обозначены Эти оси остаются неподвижными в процессе деформирования конструкции. Рассмотрим бесконечно малый элемент объема с центром в точке . Действующие на него силы обозначим . В процессе деформирования конструкции точка сместится в точку . Компоненты смещения обозначим: 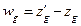. Положительные направления перемещений и сил соответствуют направлению координатных осей.

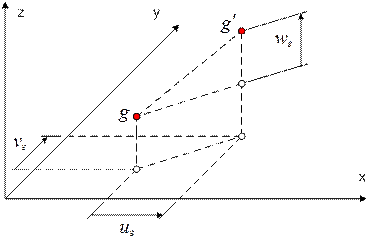
Рис. 5.1

Как говорилось в предыдущей лекции, при решении задачи расчета конструкции методом конечного обычно находятся перемещения точек тела, которые называются узловыми. Все внешние силы также заменяются сосредоточенными силами, приложенными в узлах. Таким образом, описание поведения отдельного конечного элемента осуществляется с помощью компонент сил и смещений, заданных в узловых точках элемента.

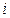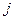Рассмотрим конечный элемент, у которого две узловые точки: и (рис. 5.2). Пусть в узле 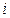приложены три узловые силы: 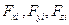. Направлению этих сил соответствуют узловые смещения 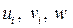, то есть в узле 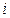- три степени свободы.

В некоторых задачах, например задачах расчета рам или балок необходимо учитывать нагрузки в виде сосредоточенных моментов и находить углы, на которые поворачиваются при деформировании поперечные сечения. Приложим в узле 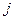три сосредоточенных момента 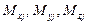Угловые смещения, соответствующие приложенным моментам, обозначим 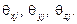Таким образом узел 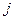также будет иметь три степени свободы.

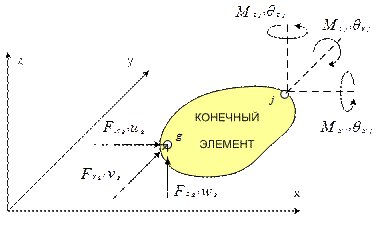
Рис. 5.2

Общее число степеней свободы элемента равно сумме степеней свободы всех узлов, то есть для данного элемента оно равно шести.

Совокупность узловых сил и узловых перемещений изображенного на рис. 5.2 конечного элемента представим соответствующими векторами: вектором узловых сил 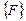и вектором узловых перемещений :

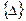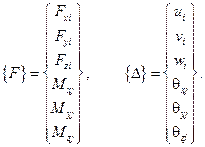(5.1-5.2)

В дальнейшем для экономии места векторы-столбцы часто будем записывать в транспонированной форме, то есть в виде матрицы-строки. Например:

.

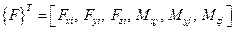Отдельную 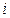-ю компоненту вектора узловых перемещений 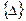будем называть 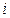-й степенью свободы.

В методе конечных элементов следует различать глобальные и локальные системы координат. Глобальные оси (оси 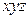на рис. 5.3) задаются для всей конструкции. Локальные системы координатмогут относиться к отдельному элементу (оси 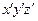на рис. 5.3) или даже к отдельному узлу (оси 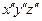на рис. 5.3). Локальные координаты используют обычно при формулировке уравнений, относящихся к одному элементу. Получив эти уравнения, можно легко преобразовать силы и перемещения к глобальной системе координат. Глобальная система координат нужна для получения уравнений, описывающих поведение всей конструкции.

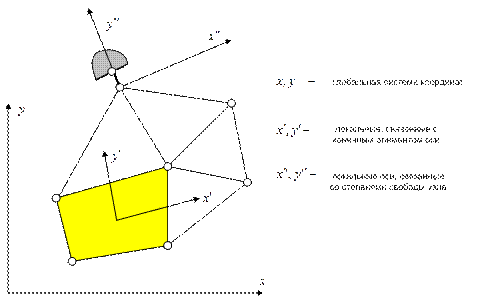
Рис. 5.3

Порядок нумерации узлов в конечном элементе традиционно направлен против часовой стрелки (рис. 5.4).

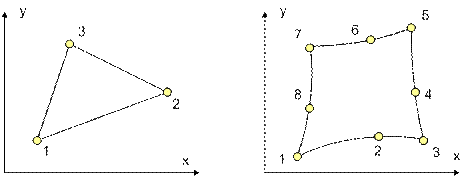
Рис. 5.4