Соотношения между силами и перемещениями для элемента

Соотношения между узловыми силами и узловыми перемещениями записываются в одном из трех основных видов: (1) уравнения жесткости, (2)уравнения податливости, (3) смешанные соотношения между силами и перемещениями.

Уравнения жесткости для элемента являются линейными алгебраическими уравнениями, которые записываются в виде

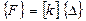, (5.3)

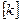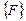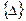где - квадратная матрица жесткости элемента, а и соответственно векторы сил и смещений для элемента.

Отдельный элемент k_ij матрицы жесткости, стоящий на пересечении 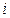-й строки и 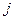-го столбца, назовем коэффициентом жесткости элемента. Легко заметить, что если перемещение 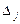положить равным единице, а все остальные перемещения приравнять к нулю, то значение силы 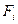станет равным .

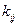На рис. 5.5 изображен пример, когда перемещение, отвечающее 4-й степени свободы равно единице, то есть 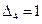, а перемещения, соответствующие остальным степеням свободы, равны нулю, так как узлы по этим направлениям закреплены. В этом случае столбец узловых сил равен столбцу коэффициентов матрицы жесткости, то есть

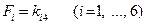
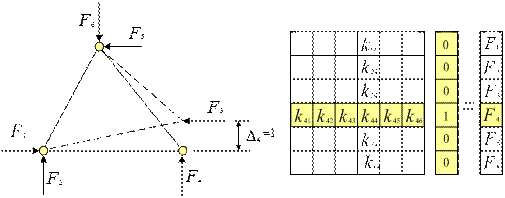
Рис. 5.5

При этом 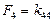можно рассматривать как силу, обеспечивающую единичное смещение 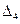по оси 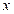первого узла, а остальные компоненты вектора 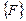- как реакции, возникающие в опорных связях при таком смещении. По этой причине четвертый столбец матрицы жесткости (как и любой другой) будет представлять собой систему уравновешенных сил.

Уравнения податливости для закрепленного элемента выражают узловые перемещения через узловые силы. Но соотношения податливости можно записать только для закрепленных неподвижно элементов, иначе при приложении сил будут возникать бесконечные перемещения тела как жесткого целого. В этом легко убедиться, попытавшись просто обратить матрицу жесткости. Отсюда следует, что для элемента можно записать столько вариантов уравнений податливости, сколько существует вариантов его неподвижного закрепления. Обычно рассматривают лишь статически определимые варианты закрепления. Если обозначить незакрепленные степени свободы и соответствующие им узловые силы индексом f, то можно записать общий вид уравнений податливости:

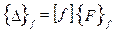, (5.4)

где 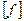- один из возможных вариантов матрицы податливости, 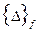- вектор незакрепленных степеней свободы, 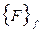- вектор соответствующих узловых сил.

Рис.5.6

Рассматривая известные соотношения для стержневого элемента, изображенного на рис. 5.6, а именно

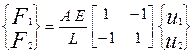, (5.5)

можно заметить, что соотношения податливости возможны в двух вариантах. При закреплении левого узла и исключении из системы компонентов содержащих индекс равный 1 мы получаем одно единственное уравнение податливости 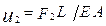. Соответственно, при закреплении правого узла и исключении из уравнений относящихся ко второй степени свободы компонентов, мы получим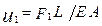

Для балочного элемента (рис. 5.7а), матрица жесткости которого имеет вид

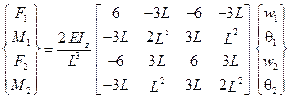, (5.6)

можно подобрать два возможных вида закрепления: свободное опирание (рис.5.7b), при котором соотношения податливости получаются в виде

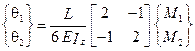(5.7)

и консольное закрепление (рис.5.7c), при котором они выглядят иначе:

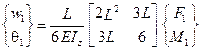(5.8)

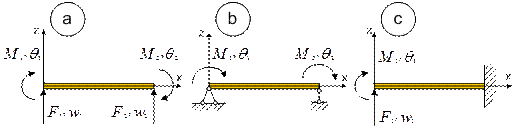
Рис. 5.7

Смешанные соотношения между силами и перемещениями устанавливают соотношения между векторами, имеющими в качестве компонент как силы, так и перемещения. Если степени свободы разбиты на две группы, обозначенные соответственно индексами f и s, то общей вид смешанных соотношений можно записать формулой

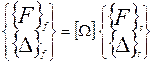. (5.9)

В частности, такой вид соотношений очень удобно использовать для установления связи между силами и перемещениями, возникающими на одном конце стержня с силами и перемещениями, действующими на другом конце. Например, для балки, изображенной на рис. 5.7а можно записать:

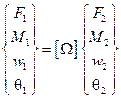(5.10)

В этом случае матрица 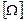называется передаточной матрицей.