Работа и энергия

Работа 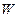силы равна произведению величины силы на величину перемещения точки приложения в направлении действия силы. Если сила увеличивается постепенно от нуля до своего конечного значения, то, проинтегрировав совершенную работу, получим следующее для нее выражение:

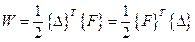(5.11)

Из рис. 5.8 видно, что отдельно взятая сила 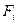на соответствующем ей перемещении 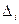совершает работу, равную заштрихованной области.

Рис. 5.8

В процессе деформирования совершенная работа преобразуется в потенциальную энергию деформаций .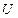

Соотношение (5.11) можно преобразовать таким образом, чтобы оно содержало только перемещения или только силы, используя для этого уравнения жесткости (5.3) или уравнения податливости (5.4).

Можно показать, что в одном случае мы получим энергию деформации элемента:

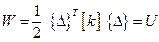, (5.12)

а в другом – дополнительную энергию деформаций:

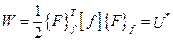, (5.13)

которые, как известно равны, если соблюдается закон Гука, то есть если материал деформируется линейно упруго.

Видно, что величина 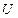является квадратичной функцией параметра , а , в свою очередь, квадратичной функцией параметра .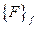

Полезно отметить, что всем возможным формам соотношений податливости, записанных для одного и того же элемента, соответствует одна и та же дополнительная энергия деформаций. В этом можно убедиться, вычислив по формуле (5.13) величину дополнительной энергии для балок , изображенных на рис. 5.7b и рис. 5.7c. Соотношения податливости для указанных балок выражены формулами (5.7) и (5.8).