Основные операции над матрицами.
· Равенство матриц.
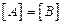 , если для всех i и j
, если для всех i и j  .
.
· Сумма матриц и разность матриц.
 если для всех i и j
если для всех i и j 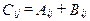 ,
,
 если для всех i и j
если для всех i и j 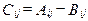 .
.
· Умножение матрицы на скаляр.
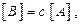 если для всех i и j
если для всех i и j 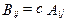 .
.
· Умножение матриц.
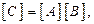
Выполняется путем вычисления каждого элемента матрицы 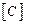 по следующему правилу:
по следующему правилу:

Следует обратить внимание, что эта операция возможна только в том случаe, когда число столбцов первой матрицы равно числу строк второй, то есть когда
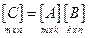 .
.
Процесс вычисления элемента матрицы 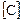 , лежащего на пересечении i-й строки и j-го столбца (то есть элемента
, лежащего на пересечении i-й строки и j-го столбца (то есть элемента 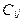 ) можно пояснить схемой:
) можно пояснить схемой:

Характерно, что 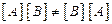 , за исключением специальных случаев.
, за исключением специальных случаев.
Могут не совпадать даже размерности получаемых матриц. Так, при перемножении матрицы-строки на матрицу-столбец результатом будет скаляр (матрица размером 1 x 1), а при перемножении матрицы-столбца на матрицу-строку результатом будет прямоугольная матрица.
Один из частных случаев, когда умножение матриц коммутативно, – умножение на единичную матрицу. Легко показать, что  .
.
Интересно отметить также, что произведение  может быть равно нулю, даже если сомножители не являются нулевыми матрицами.
может быть равно нулю, даже если сомножители не являются нулевыми матрицами.
Например,  .
.
· Обратные матрицы.
Обратная матрица  есть такая матрица, для которой выполняется равенство
есть такая матрица, для которой выполняется равенство
 .
.
Не всякая матрица имеет обратную. Если матрица имеет обратную, то говорят, что она невырожденная. Матрицы, не имеющие обратной матрицы, называются вырожденными или особенными. Определитель вырожденной матрицы равен нулю, то есть
 .
.
Следующие высказывания означают одно и то же:
§ матрица 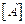 - невырожденная,
- невырожденная,
§ обратная матрица 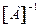 существует,
существует,
§ столбцы матрицы 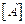 линейно независимы,
линейно независимы,
§ строки матрицы 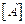 линейно независимы.
линейно независимы.
Можно показать, что обратная матрица произведения нескольких матриц определяется по правилу:
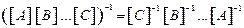 .
.
· Транспонирование матриц.
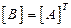 .
.
Транспонированная матрица 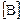 получается путем замены в исходной матрице
получается путем замены в исходной матрице 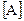 строк столбцами. В частности, транспонирование матрицы-столбца дает матрицу-строку и наоборот.
строк столбцами. В частности, транспонирование матрицы-столбца дает матрицу-строку и наоборот.
Транспонирование произведения нескольких матриц выполняется по правилу:
 .
.
· Дифференцирование и интегрирование матриц.
Если элементами матрицы  являются функции
являются функции 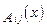 , то можно условно определить производную от нее следующим образом:
, то можно условно определить производную от нее следующим образом:
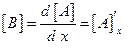 , если для всех элементов матрицы
, если для всех элементов матрицы  .
.
Частные производные и интегралы от матрицы можно понимать аналогично.
· Нахождение собственных чисел (значений) и собственных векторов квадратной матрицы.
Если в выражении 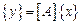 матрицы-столбцы рассматривать как вектора, то матрица
матрицы-столбцы рассматривать как вектора, то матрица 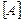 будет представлять собой линейный оператор, преобразующий вектор
будет представлять собой линейный оператор, преобразующий вектор 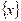 в вектор
в вектор  , имеющий в общем случае (см. рис. 2.2) иную длину и иное направление, нежели вектор
, имеющий в общем случае (см. рис. 2.2) иную длину и иное направление, нежели вектор 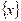 . Более того, если матрица
. Более того, если матрица 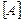 не является квадратной, исходный вектор
не является квадратной, исходный вектор 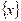 и полученный вектор
и полученный вектор  могут принадлежать пространствам с разным числом измерений, то есть иметь различное число компонент. Преобразование же вида
могут принадлежать пространствам с разным числом измерений, то есть иметь различное число компонент. Преобразование же вида 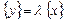 изменяет лишь длину вектора, но не изменяет его направления.
изменяет лишь длину вектора, но не изменяет его направления.
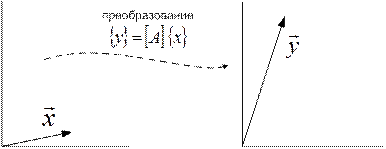
Рис. 2.2

Рис. 2.3
Если удается установить равенство вида 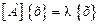 , то это означает, что линейный оператор
, то это означает, что линейный оператор 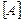 в данном частном случае также изменяет лишь длину вектора, не меняя его направления.
в данном частном случае также изменяет лишь длину вектора, не меняя его направления.
Собственные значения (собственные числа) матрицы  - это такие числа
- это такие числа  , для которых выполняется равенство
, для которых выполняется равенство 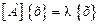 для некоторого ненулевого столбца (вектора)
для некоторого ненулевого столбца (вектора) 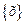 . Вектор
. Вектор 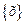 в этом случае называется собственным вектором матрицы
в этом случае называется собственным вектором матрицы  ( рис. 2.3).
( рис. 2.3).
Квадратная матрица порядка n имеет n собственных чисел и, как правило, (не всегда) n собственных векторов.
Дата добавления: 2015-01-02; просмотров: 842;
