Повне прискорення точки дорівнює векторній сумі її дотичного і нормального прискорень.

Для доведення цієї теореми згадаємо, що при натуральному способі вектор швидкості точки визначається за формулою:

.

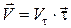Оскільки кожен з співмножників змінюється за часом, то вектор прискорення точки дорівнює:

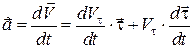. (13.5)

Будемо розглядати орт 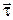як складну функцію часу:

,

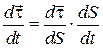Використовуючи (13.3) і пам’ятаючи, що 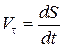, отримаємо:

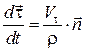. (13.6)

Підставляючи у (13.5) значення 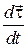з (13.6) і враховуючи, що квадрат проекції швидкості на дотичну дорівнює квадрату модуляшвидкості V, одержимо таку формулу розкладу вектора прискорення точки за натуральними осями:

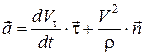. (13.7)

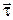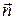Із (13.7) видно, що вектор прискорення складається з двох складових за напрямами і , тобто він лежить у стичній площині.

Проекція 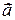на бінормаль дорівнює нулю.

Складова прискорення за напрямом дотичної

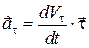(13.8)

називається дотичним (тангенціальним) прискоренням. Воно характеризує зміну модуля швидкості.

Складова прискорення за напрямом головної нормалі

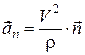(13.9)

називаєтьсянормальним прискоренням. Воно характеризує зміну швидкості за напрямом.

Таким чином, повний вектор прискорення дорівнює:

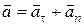. (13.10)

Проекції прискорення точки на натуральні осі – дотичну та головну нормаль - визначаються за відповідними формулами:

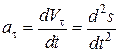; (13.11)

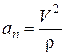. (13.12)

Модуль вектора прискорення точки, враховуючи що 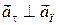, дорівнює:

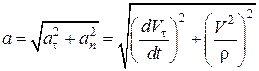. (13.13)

Напрям вектора прискорення визначається тангенсом кута 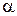, утвореного векторами повного і нормального прискорень (рис. 12.2):

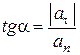. (13.14)